前面三题只贴代码，第四题详细题解

A

#include<iostream>
#include<algorithm>
#include<string.h>
using namespace std;
#define debug(x) cout<<"[debug]"#x<<"="<<x<<endl;
const int N=105;
int a[N];
int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        int n,k;
        scanf("%d%d",&n,&k);
        for(int i=1;i<=n;i++)
        {
            scanf("%d",&a[i]);
        }
        int res=0;
        for(int i=0;i<k;i++)
        {
            int q=0,w=0;
            for(int j=1;j<=n;j++)
            {
                if((a[j]>>i)&1)
                q++;//1
                else
                w++;//0
            }
            if(q>=w)
            res+=1<<i;
        }
        printf("%d\n",res);
    }
}

B

#include<iostream>
#include<algorithm>
#include<string.h>
using namespace std;
#define debug(x) cout<<"[debug]"#x<<"="<<x<<endl;
const int N=150005;
int a[N];
struct lwy
{
    int l;
    int r;
}b[N];
int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        int res=-1;
        memset(b,0,sizeof b);
        int n;
        scanf("%d",&n);
        for(int i=1;i<=n;i++)
        {
            scanf("%d",&a[i]);

            int x=a[i];
            if(b[x].l==0)
            {
                b[x].l=i;
            }
            else if(b[x].r==0)
            {
                b[x].r=i;
                int ans=b[x].l+(n-b[x].r);
                res=max(res,ans);
            }
            else
            {
                b[x].l=b[x].r;
                b[x].r=i;

                int ans=b[x].l+(n-b[x].r);
                res=max(res,ans);
            }
        }
        printf("%d\n",res);
    }

}

C

#include<iostream>
#include<algorithm>
#include<string.h>
using namespace std;
#define debug(x) cout<<"[debug]"#x<<"="<<x<<endl;
const int N=505;
int p[N];
int t[N];
int dp[N][N];
int main()
{
    int n,len,m;
    scanf("%d%d%d",&n,&len,&m);

    for(int i=0;i<n;i++)
    scanf("%d",&p[i]);

    for(int i=0;i<n;i++)
    scanf("%d",&t[i]);

    p[n]=len;
    memset(dp,0x3f,sizeof dp);

    dp[0][0]=0;
    for(int i=0;i<=n;i++)
    {
        for(int j=0;j<i;j++)
        {
            for(int k=m;k>=i-j-1;k--)
            {
                dp[i][k]=min(dp[i][k],dp[j][k-(i-j-1)]+(p[i]-p[j])*t[j]);
            }
        }
    }
    int res=0x3f3f3f3f;
    for(int i=0;i<=m;i++)
    {
        res=min(res,dp[n][i]);
    }
    printf("%d\n",res);
}

D

题目大意：给定你n和k。要求你从n个数中找到尽可能多的数，使他们两两异或起来都不小于k。若找到的数不超过两个，输出-1

（为方便理解，我们不妨设k的最高位为m）

首先我们可以证明出所有的数字中，m+1~29位都相同的数字，我们最多可以选2个。

证明如下图（抽屉原理）
x和y的m+1~29位异或起来都会为0，则必然有第m位分别为0和1，此时若有第三个数z。则z的第m位不管为0还是1，必然会和前两个数中的某个数异或起来m位为0，导致结果小于k

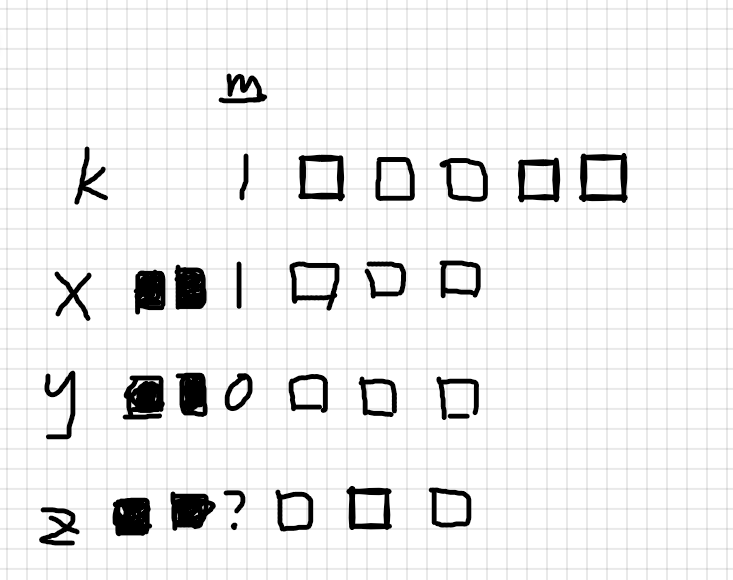
因此，我们可以把高位（指m+1~29位）都相同的数字归为一组。因为每一组都是相互独立的，然后我们分别从每一组中找到两个$\bigoplus$起来大于等于k的数。

问题是：怎么从一组中找到两个数异或起来≥k呢
我们可以采用trie树的方法。因为它是通过分治的方法，最终找到最大异或对，查找每一个数的最大异或对的复杂度为logn
所以总复杂度为nlogn
- trie树具体解释

**从trie树找到与x异或起来最大的数。**
trie树是从高位开始往下建的。
我们查找最大异或对的时候从高位开始，若x的当前位为1，则我们就遍历0的这一边。若没有0的子树，则只能将就着走1的子树。最终走完全程即可，得到的数答案就是最大的
具体请看y总算法基础课的最大异或对：https://www.acwing.com/problem/content/145/

一些其它的细节问题：
可以用map实现遍历分组（第一次用map实现qaq）
然后遍历每一组的时候，记得先把trie树清空。
若找不到两个数$x\bigoplus y \geq k$，则随便取一个数即可。因为可以证明它必然与其它组所有数异或都会大于k。（因为异或起来必然有m+1~29位）

代码如下

#include<iostream>
#include<algorithm>
#include<string.h>
#include<vector>
#include<map>
#include<unordered_map>
using namespace std;
#define debug(x) cout<<"[debug]"#x<<"="<<x<<endl;
const int N=300005;
int a[N];
int son[N*30][2],idx;
map<int,vector<int>> mp;//存同一组的所有蜘蛛下标
map<int,vector<int>>::iterator iter;
map<int,int> id;//存每个值对应的下标
vector<int> res;
int get(int k)
{
    int res=0;
    while(k)
    {
        k>>=1;
        res++;
    }
    return res;
}
void insert(int x)
{
    int p=0;
    for(int i=29;i>=0;i--)
    {
        int u=x>>i&1;
        if(!son[p][u]) son[p][u]=++idx;

        p=son[p][u];
    }
}
int query(int x)
{
    int p=0;
    int ans=0;
    for(int i=29;i>=0;i--)
    {
        int u=x>>i&1;
        if(son[p][u^1])
        {
            ans=(ans<<1)+(u^1);
            p=son[p][u^1];
        }
        else
        {
            ans=(ans<<1)+u;
            p=son[p][u];
        }
    }
    return ans;
}
int main()
{
    int n,k;
    scanf("%d%d",&n,&k);
    int m=get(k);//得到k的最大位数是第几位
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&a[i]);

        int x=a[i]>>m;
        mp[x].push_back(a[i]);//将m+1~29位数相同的归为一组
        id[a[i]]=i;
    }
    //特判一下k=0的情况，因为我的mp相同值只能存一个下标,异或为0答案也要存的话会出错
    if(k==0)
    {
        printf("%d\n",n);
        for(int i=1;i<=n;i++)
        printf("%d ",i);
        return 0;
    }
    for(iter=mp.begin();iter!=mp.end();iter++)
    {
        memset(son,0,sizeof (int)*2*(idx+3));//清空trie树
        idx=0;
        vector<int> p=iter->second;//得到该组
        int l=-1,r=-1;//存答案，存从该组中拿两个的情况
        int gg=-1;//存拿一个的情况,则这个一定会拿（因为它一定和其它组异或>=k）
        for(int i=0;i<p.size();i++)
        {
            int x=p[i];
            //debug(x);
            gg=id[x];
            insert(x);//将该数字插入trie树
            int t=query(x);//找到与x相匹配最大的异或对
            if((t^x)>=k)
            {
                l=id[x];
                r=id[t];
                break;
            }
        }
        if(l>0&&r>0)
        {
            res.push_back(l);
            res.push_back(r);
        }
        else if(gg>0)
        res.push_back(gg);
    }

    if(res.size()<=1) puts("-1");
    else
    {
        printf("%d\n",res.size());
        for(int i=0;i<res.size();i++)
        {
            printf("%d ",res[i]);
        }
    }
}