1.枚举中心法

class Solution {
public:
    string longestPalindrome(string s) {
        string res;
        for( int i=0; i<s.size(); i++ )  // 枚举中心点
        {
            int l = i-1, r = i+1;  // 奇数情况
            while( l>=0 && r<s.size() && s[l]==s[r] ) l--,r++;
            if( res.size() < r-l-1 ) res = s.substr(l+1,r-l-1);  // 子串长度 = (r-1)-(l+1) + 1

            l = i, r = i+1;  // 偶数情况
            while( l>=0 && r<s.size() && s[l]==s[r] ) l--,r++;
            if( res.size() < r-l-1 ) res = s.substr(l+1,r-l-1); 
        }
        return res;
    }
};

2.动态规划

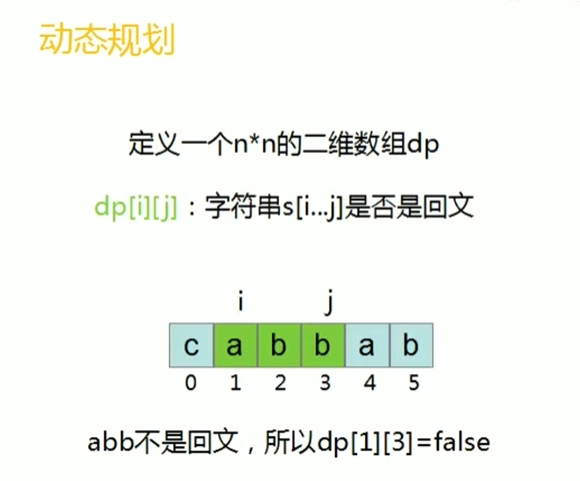
动画演示：

class Solution {
public:
    string longestPalindrome(string s) {
        int n = s.size();
        vector<vector<bool>> dp(n,vector<bool>(n,false));
        for( int i=0; i<n; i++ ) dp[i][i] = true;

        // 枚举终起点
        for( int j=0; j<n; j++ )
        for( int i=0; i<j; i++ )
        {
            if( s[i]==s[j] ) 
            {
                dp[i][j] = (j-i<3) || dp[i+1][j-1];  // 长度小于4时肯定回文
            }
            else dp[i][j] = false;
        }

        int max_len = 1;
        int st = 0;
        for( int j=0; j<n; j++ )
        for( int i=0; i<j; i++ )
        {
            if( dp[i][j] && (j-i+1)>max_len )
            {
                st = i;
                max_len = j-i+1;
            }
        }
        return s.substr(st,max_len);
    }
};