前言

前序遍历：根-左-右

中序遍历：左-根-右

后序遍历：左-右-根

一：前序遍历：根-左-右

先遍历根节点，然后 先遍历完 左子树，最后遍历右子树；在遍历左、右子树时，仍然先访问根结点，然后遍历左子树，最后遍历右子树

前序遍历 = 深搜

前序遍历结果：ABDECF（第一个是根节点）

实现：

1：递归实现

List<Integer> list = new ArrayList<>();
private static void pre(TreeNode root)
{
    if(root == null) return;
    list.add(root.val);
    dfs(root.left);
    dfs(root.right);
}

2：迭代实现

List<Integer> list = new ArrayList<>();
Stack<TreeNode> stk = new Stack<>();
private static void pre(TreeNode root)
{
    if(root == null) return;
    stk.push(root);
    while(!stk.empty())
    {
        TreeNode node = stk.pop();
        list.add(node.val);
        if(node.right != null) stk.push(node.right);    // 因为栈是先进后出，所以先加入右节点，再加入左节点
        if(node.left != null) stk.push(node.left);
    }
}

二：中序遍历：左-根-右

先遍历完左子树，然后遍历根节点，最后遍历右子树；在遍历左、右子树时，仍然先遍历左子树，然后遍历根节点，最后遍历右子树；

中序遍历结果：DBEAFC

实现：

1：递归实现

List<Integer> list = new ArrayList<>();
private static void in(TreeNode root)
{
    if(root == null) return;
    dfs(root.left);
    list.add(root.val);
    dfs(root.right);
}

2：迭代实现

List<Integer> list = new ArrayList<>();
Stack<TreeNode> stk = new Stack<>();
private static void in(TreeNode root)
{
    if(root == null) return;
    TreeNode cur = root;
    while(!stk.empty() || cur != null)
    {
        while(cur != null)     // 找到最左侧节点
        {
            stk.push(cur);
            cur = cur.left;
        }
        cur = stk.pop();
        list.add(cur.val);
        cur = node.right;
    }
}

三：后序遍历：左-右-根

先遍历完左子树，然后再遍历完右子树，最后遍历根节点；在遍历左、右子树时，仍然先遍历左子树，然后遍历右子树，最后遍历根节点

后序遍历结果：DEBFCA（最后一个一定是根节点）

实现：

1：递归实现

List<Integer> list = new ArrayList<>();
private static void after(TreeNode root)
{
    if(root == null) return;
    dfs(root.left);
    dfs(root.right);
    list.add(root.val);
}

2：迭代实现

List<Integer> list = new ArrayList<>();
Stack<TreeNode> stk = new Stack<>();
private static void pre(TreeNode root)
{
    if(root == null) return;
    stk.push(root);
    while(!stk.empty())
    {
        TreeNode node = stk.pop();
        list.add(node.val);
        if(node.left != null) stk.push(node.left);
        if(node.right != null) stk.push(node.right);     // 根右左
    }
    Collections.reverse(list);                           // 左右根
}

四：二叉树的深度优先搜索

从 root 开始，一条路走到底，然后再退回到上一个节点，然后再走下一条路，直到所有节点都遍历完；

图解：

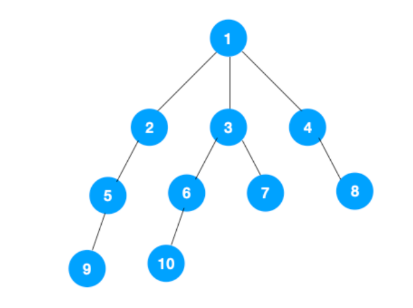
遍历顺序如下：

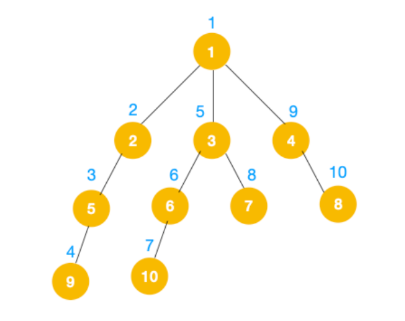
实现方式：

1：递归实现

dfs(root);

private static void dfs(TreeNode root)
{
    if(root == null) return;
    list.add(root.val);
    dfs(root.left);
    dfs(root.right);
    .....                        // 后面叫做回溯
}

2：栈实现

List<Integer> list = new ArrayList<>();
Stack<TreeNode> stk = new Stack<>();
private static void pre(TreeNode root)
{
    if(root == null) return;
    stk.push(root);
    while(!stk.empty())
    {
        TreeNode node = stk.pop();
        list.add(node.val);
        if(node.right != null) stk.push(node.right);    // 因为栈是先进后出，所以先加入右节点，再加入左节点
        if(node.left != null) stk.push(node.left);
    }
}

五：二叉树的宽度优先遍历

从 root 开始遍历，先遍历这个节点的相邻节点，然后再依次遍历相邻节点的相邻节点，也就是层序遍历

图解：

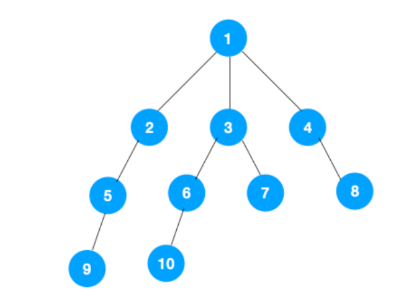
宽搜的顺序与序号相同

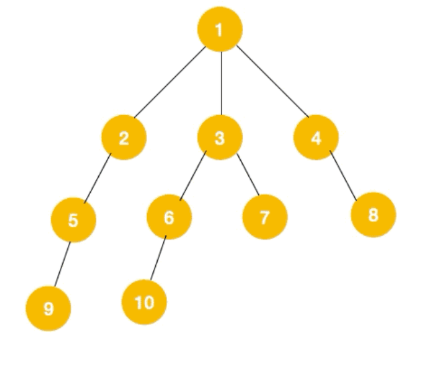
实现方式：队列实现

Queue<TreeNode> q = new LinkedList<>();

q.offer(root);
while(q.size() != 0)
{
    TreeNode node = q.poll();
    q.offer();
    .....
}