题目链接

递推法求组合数

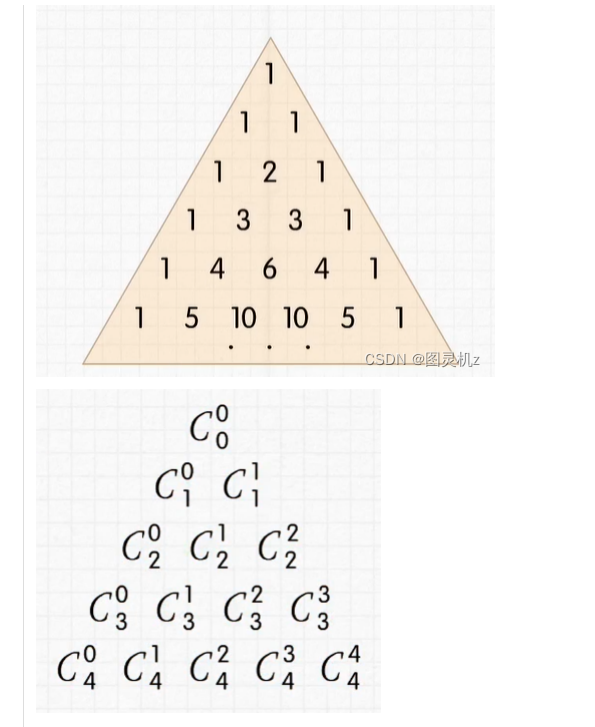
如图， 易知

1. 左右两侧斜线都是1，$C^0_n=C^n_n=1$

2. 其他数等于其左上角和右上角两数之和$$ C_{n}^{m-1}+C_{n}^{m}=C_{n+1}^{m} $$

#include <iostream>
using namespace std;

const int NN = 2010, mod = 1e9 + 7;
int n, a, b;
int c[NN][NN];

int count(int a, int b){
    int& v = c[a][b];
    if (v) return v;   // 记忆化搜索
    if (!b || a == b) return v = 1;  // 左右两条斜线都是1
    v = (count(a - 1, b - 1) + count(a - 1, b)) % mod;
    return v;
}

int main(){
    cin >> n;
    while (n --){
        cin >> a >> b;
        cout << count(a, b) << endl;
    }

    return 0;
}