题目

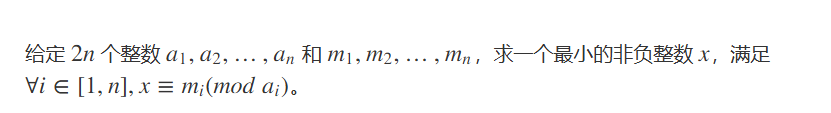
在n个方程中的两个方程
x = k1 * a1 + m1
x = k2 * a2 + m2
合并方程
k1 * a1 - k2 * a2 = m2 - m1
求解系数k1,k2, 根据exgcd可以求得
当d为(m2 - m1)的倍数时有解, 将所得系数扩大这时(m2 - m1) / d倍, 可以得到一组特解k1和k2
那么对于k1,k2的所有解为
k1 = k1 + k * (a2 / d), k2 = k2 + k * (a1 / d), 其中k为任意整数
将k1带入第一个公式(关于x的表达式)有：
x = k1 * a1 + k(a1 * a2 / d) + m1, 整理有：
x = k(a1 * a2 / d) + k1 * a1 + m1;
令a1 * a2 / d = a, k1 * a1 + m1 = m
原式=k * a + m, 也就是将两个式子合并成为一个形如题目中的式子(x % a = m)的形式
其中a就是lcm(a1, a2), m = k1 * a1 + m1, 像这样不断更新a和m的值即可
最后合并成为一个式子：
x = k * a + m, 求解满足条件的最小的正整数x就是m % a的正余数

值得注意的是exgcd求解的是k1和-k2, 因为这里并没有对k2进行操作因此并没有出现错误

acwing模版应用

import java.util.*;

public class Main {

    public static void main(String[] args) {

        Scanner sc = new Scanner(System.in);
        boolean flag = true;
        int n = sc.nextInt();
        long a1 = sc.nextLong(), m1 = sc.nextLong();
        for (int i = 0; i < n - 1; i++) {
            long a2 = sc.nextLong(), m2 = sc.nextLong();
            long[] k1 = new long[1], k2 = new long[1];
            long d = exgcd(a1, a2, k1, k2);
            if ((m2 - m1) % d != 0) {//这里的无所谓
                flag = false;
                break;
            }
            k1[0] *= (m2 - m1) / d;//m2和m1的位置不能颠倒,如果颠倒需要对k1取负数
            long t = a2 / d;
            k1[0] = (k1[0] % t + t) % t;//确保不会爆long, 直接取最小的正整数解
            //更新m1和a1
            m1 = k1[0] * a1 + m1;
            a1 = a1 / d * a2;
        }

        if (flag) {//取最小正整数解
            System.out.println((m1 % a1 + a1) % a1);
        } else {
            System.out.println(-1);
        }
    }

    static long exgcd(long a, long b, long[] x, long[] y) {
        if (b == 0) {
            x[0] = 1;
            y[0] = 0;
            return a;
        }
        long d = exgcd(b, a % b, y, x);
        y[0] -= a / b * x[0];
        return d;
    }
}