满足条件的01序列

卡特兰数 —— 模板题 AcWing 889. 满足条件的01序列
给定n个0和n个1，它们按照某种顺序排成长度为2n的序列，满足任意前缀中0的个数都不少于1的个数的序列的数量为： Cat(n) = C(2n, n) / (n + 1)

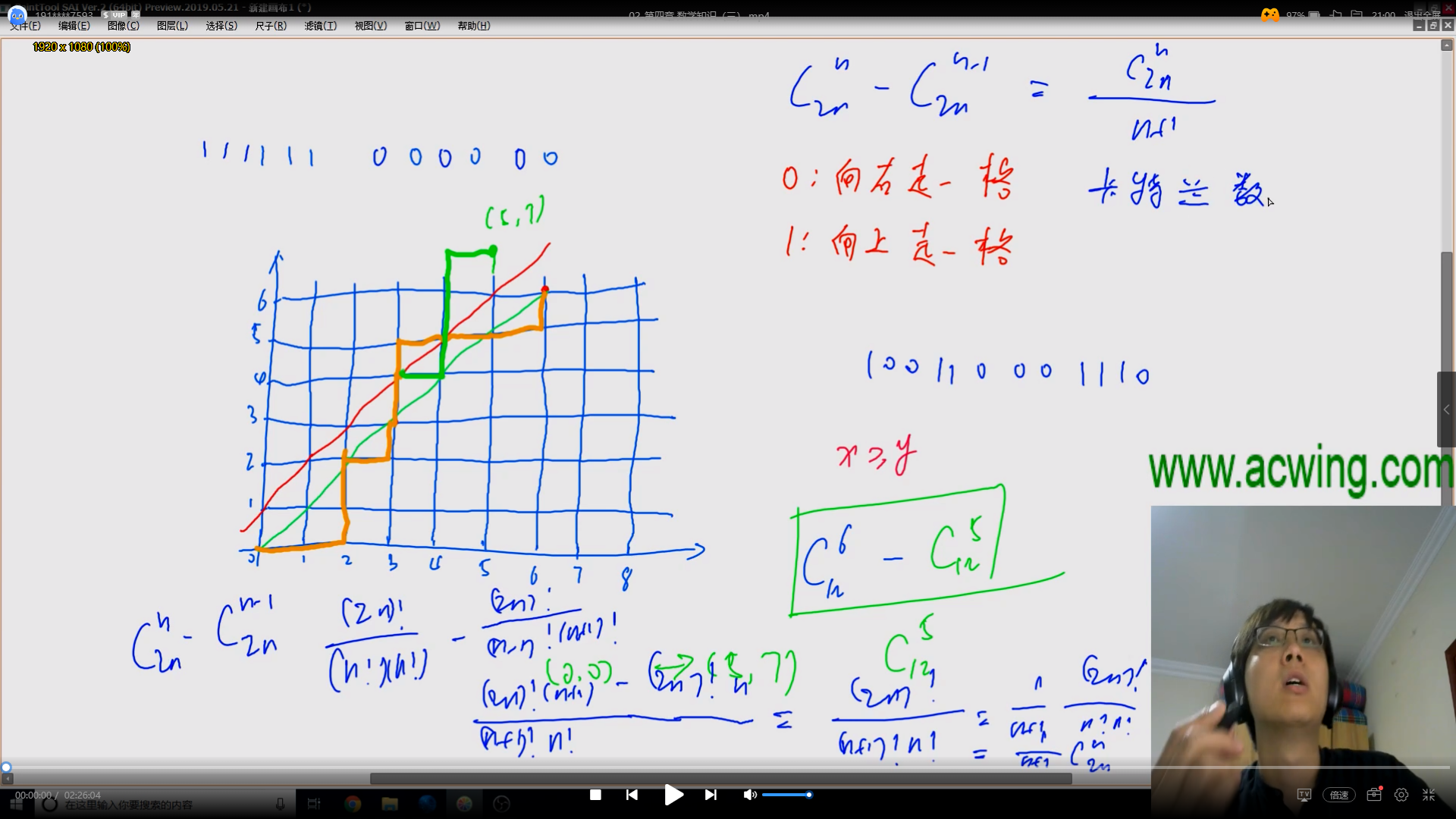
卡特兰数的推导过程见下图，y总讲得简介易懂，一目了然(๑•̀ㅂ•́)و✧

但还是对着图片补充一下，$C_{2n}^{n}$ 是从 (0,0) 走到 (n,n)的所有路径总数，$C_{2n}^{n-1}$是从(0,0)到(n-1,n+1)的所有路径数量（也就是所有从 (0,0) 走到 (n,n)经过了红色斜线的路径数量，也就是所有不符合条件的路径数量）。两者相减，便是符合条件的路径数量（也就是严格不经过红线的路径数量）

#include <iostream>
using namespace std;

typedef long long ll;
const int mod = 1e9 + 7;
int n, res = 1;

int qmi(int a, int m, int p){
    int res = 1;
    while (m){
        if (m & 1) res = (ll)res * a % mod;
        a = (ll)a * a % mod;
        m >>= 1;
    }return res;
}

int main(){
    cin >> n;
    int a = 2 * n, b = n;
    for (int i = a, b = 1; b <= n; a --, b ++){
        res = (ll)res * a % mod * qmi(b, mod - 2, mod) % mod;
    }
    res =  (ll)res * qmi(n + 1, mod - 2, mod) % mod;
    cout << res;

    return 0;
}