1.给定一个度数序列{d}，判断是否可以根据这个度数序列构造出简单无向图。

Havel–Hakimi algorithm：
一个度数序列可以构成简单无向图，当且仅当将这个序列{d}降序排序之后，将d1后面的d1个数−1，并将d1从序列中除去，形成的新度数序列没有负数，且新的度数序列可以构成简单无向图。
于是我们发现，利用这个方法递归地判断，最后一定以出现负数或者全零序列结束，时间复杂度Θ($n^2$)，同时我们可以根据这个算法构造出图的邻接矩阵。
2.一个度数序列可以构成无向图，当且仅当将{d}降序排序之后：

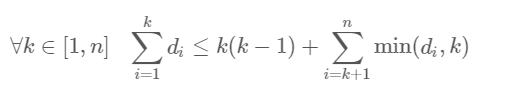
时间复杂度Θ(n)，但是这种算法只可以进行判定，不可以构造出具体的图。
为了方便记忆，我们可以这样粗略地理解式子的含义：一段前缀他们的度数可以通过自己内部的k个点互相连边和后面的n−k+1个点来贡献。
转自：https://www.cnblogs.com/ylsoi/p/10206112.html
例题：http://acm.zzuli.edu.cn/problem.php?id=1453
例题代码：

#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
#define endl "\n"
using namespace std;
const int N = 1e4 + 10;
int d[N],s[N],sd[N],n;
void solve(){
    for(int i = 1 ; i <= n ; ++i) cin >> d[i];
    sort(d + 1,d + n + 1);
    reverse(d + 1,d + n + 1);
    s[n + 1] = 0;
    for(int i = n; i >= 1 ; --i){
        s[i] = s[i + 1] + d[i];
    }
    int k = n;
    sd[0] = 0;
    for(int i = 1 ; i <= n ; ++i){
        sd[i] = sd[i - 1] + d[i];
        while(k && d[k] < i) k--;
        int t;
        if(k > i) t = k;
        else t = i;
        int sum = s[t + 1] + (t - i) * i;
        if(sd[i] > (i - 1) * i + sum){
            cout << "NO" << endl;
            return;
        }
    }
    cout << "YES" << endl;
}

signed main(){
    IOS;
    while(cin >> n)
    solve();
    return 0;
}