什么是计算几何

• 计算几何 Computational Geometry
• 研究几何形体的计算机表示、分析与综合
• “计算几何” —— 以计算为主的几何

计算几何题的特点

• 题目比较长
• 图形抽象，需要良好的数学基础和空间想象能力
• 有许多容易忽视的特殊情况，而且往往需要单独处理，代码量大
• 需要考虑浮点运算时产生的精度误差
• 可以与其他类型的题目结合，从而更加复杂
• 常作为压轴题目出现在程序设计竞赛中

基础 —— 点线面

用矢量描述计算几何中的基本元素

几何图形的表示

• 沿用解析几何中的表示方法？
• 点 $P(x, y, z)$
• 线 $x = a_x t + b_x$，$y = a_y t + b_y$，$z = a_z t + b_z$
• 面 $ax + by + cz + d = 0$

但特殊情况太多，有没有更好的办法？

矢量法

• 表示简单
• 功能强大
• 特殊情况少，思维难度较低
• 函数可重复利用（即所谓的“模版”）
• 尽可能避免除法和三角函数，精度高，效率高

矢量表示

class CVector {
    double x, y;
};

表示从 $0$ 点到 $(x, y)$ 的矢量。对矢量只关心方向和长度，不关心（位置）起点和终点。

矢量的基本运算

CVector operator + (CVector p, CVector q) {
    return CVector(p.x + q.x, p.y + q.y);
}

用法：c = a + b; // a, b, c 都是 CVector 对象

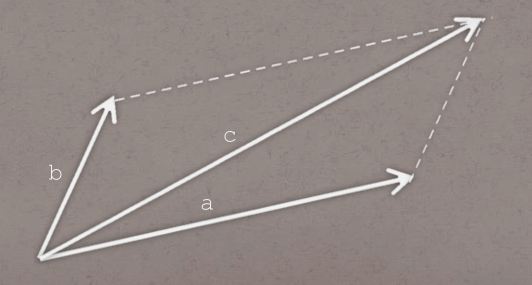
CVector operator - (CVector p, CVector q) {
    return CVector(p.x - q.x, p.y - q.y);
}

用法： c = a - b; // a, b, c 都是 CVector 对象

CVector operator * (double k, CVector p) {
    return CVector(k * p.x, k * p.y);
}

用法：c = f * a; // a 是 CVector 对象，f 是double

$c$ 方向与 $a$ 相同， $|c| = f * |a|$

矢量的点积

性质：$p \cdot q = |p| |q| \cos <p, q\>$

double operator * (CVector p, CVector q) {
    return p.x * q.x + p.y * q.y;
}

$a$ 与 $b$ 的点积，就是 $a$ 的模乘以 $b$ 在 $a$ 上投影的模。若投影与 $a$ 方向相反则为负值

• 功能：求同向还是异向；求投影；求出投影后用勾股定理求点到直线距离；

用法：double c = a * b; // a, b 都是 CVector 对象

• 若 $a * b = 0$，则 $a$ 和 $b$ 垂直

矢量的模长

• 用矢量与自身点积求模

double length(CVector p) {
    return sqrt(p * p);
} // 求矢量的模 

矢量单位化

• 用矢量除以自身的长度以得到同方向的单位矢量

CVector unit(CVector p) {
    return 1 / length(p) * p;
}

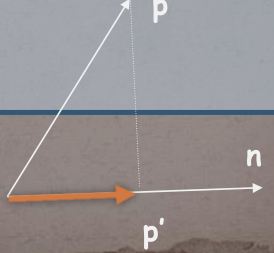
矢量的投影长度

• 矢量与该方向单位矢量的点积
• 注意：负数表示反方向

double project(CVector p, CVector n) {
    return dot(p, unit(n)); // 点积 
}
double dot(CVector p, CVector q) {
    return p.x * q.x + p.y * q.y;
}

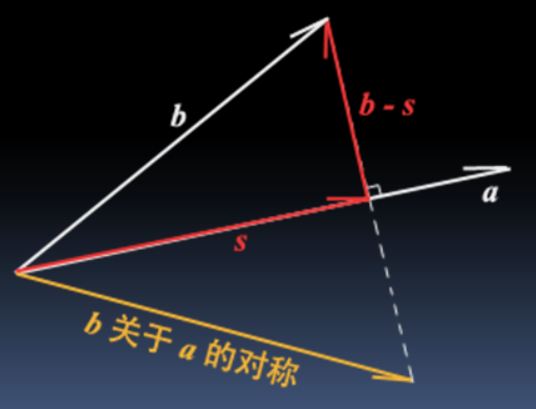
矢量的点积

$b$ 在 $a$ 上的投影的“模”是 $\frac{a \cdot b}{|a|}$
所以 $b$ 在 $a$ 上的投影即为 $\frac{a \cdot b}{|a|}\frac{a}{|a|} = a\frac{a \cdot b}{a^2}$

记 $b$ 在 $a$ 上的投影为 $s = a\frac{a \cdot b}{a^2}$
则 $b$ 关于 $a$ 的对称为 $b - 2(b - s) = 2s - b = 2a\frac{a \cdot b}{a^2} -b$。

矢量的叉积（外积、向量积）

设 $A$、$B$ 为向量
表示方式：$A \times B$

$A = (x_1, y_1, z_1), \ B = (x_2, y_2, z_2)$

$ A \times B = \left| \begin{matrix} i & j & k \\\ x_1 & y_1 & z_1 \\\ x_2 & y_2 & z_2 \\\ \end{matrix} \right| = \left( y_1{z_2} - y_2{z_1} \right)i + \left( {x_2}{z_1} - {x_1}{z_2} \right)j + \left( {x_1}{y_2} - {x_2}{y_1} \right)k $

$ i = (1, 0, 0) \ j = (0, 1, 0) \ k = (0, 0, 1) $

亦即 $A \times B = \left( {y_1}{z_2} - {y_2}{z_1},{x_2}{z_1} - {x_1}{z_2},{x_1}{y_2} - {x_2}{y_1} \right)$

大小：$|A \times B| = |A||B| \sin < A,B >$

性质：

1. $A \times B = -B \times A$
2. $(A + B) \times C = A \times C + B \times C$

功能：求面积；求顺时针方向还是逆时针方向；判断是否在半平面上

double operator ^(CVector p, CVector q) {
    return p.x * q.y - q.x * p.y;
}

// 函数形式 
double Cross(CVector p, CVector q) {
    return p.x * q.y - q.x * q.y;
}

用法：

c = a ^ b; // a, b, c都是 CVector 对象 

$a \times b$ 为有向面积，可正可负
若 $a$ 逆时针旋转小于 $180$ 度，则结果为正，否则结果为负

例题1： Scrambled Polygon

乱序给出凸多边形的顶点坐标，要求按逆时针顺序输出各顶点。给的第一个点一定是 $(0, 0)$，没有其他点在坐标轴上，没有三点共线的情况。

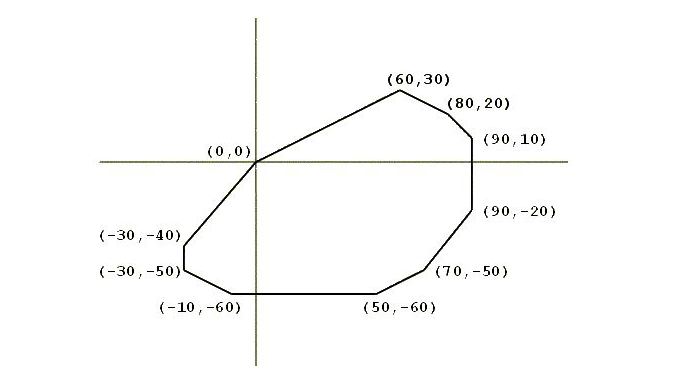
分析：

利用叉积排序

C++ 代码

#include <bits/stdc++.h>

using std::cin;
using std::cout;

struct Vector {
    double x, y;
    Vector(int xx, int yy): x(xx), y(yy) {}
    Vector() {}
    double operator^(const Vector &v) const {
        return x*v.y - v.x*y;
    }
};

#define Point Vector

// 从 A 点指向 B 点的向量可用 B-A 来表示 
Vector operator-(const Point &p1, const Point &p2) {
    // 向量从 p2 指向 p1 
    return Vector(p1.x - p2.x, p1.y - p2.y);
}

// 如果 p1^p2>0，说明 p1 经逆时针旋转<180度可以到 p2 ，则 p1<p2 
bool operator<(const Point &p1, const Point &p2) {
    if ((Vector(p2 - Point(0, 0)) ^ Vector(p1 - Point(0, 0))) > 0)
        return true;
    return false;
}

Point ps[60];

int main() {
    int x, y;
    int n = 0;
    while (cin >> ps[n].x >> ps[n].y) ++n;

    std::sort(ps+1, ps+n);

    puts("(0,0)");
    for (int i = n-1; i > 0; --i) {
        printf("(%d,%d)\n", (int)ps[i].x, (int)ps[i].y);
    }

    return 0;
}

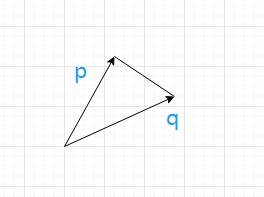
两个矢量所围成的三角形面积

• 两个矢量叉积的一半
• 注意：得到的面积可能为有向面积，可能为负

double area(CVector p, CVector q) {
    return p^q / 2;
}