题意:给n个矩形,求n个矩形合并后的周长是多少
周长的计算更复杂些,看这张图:
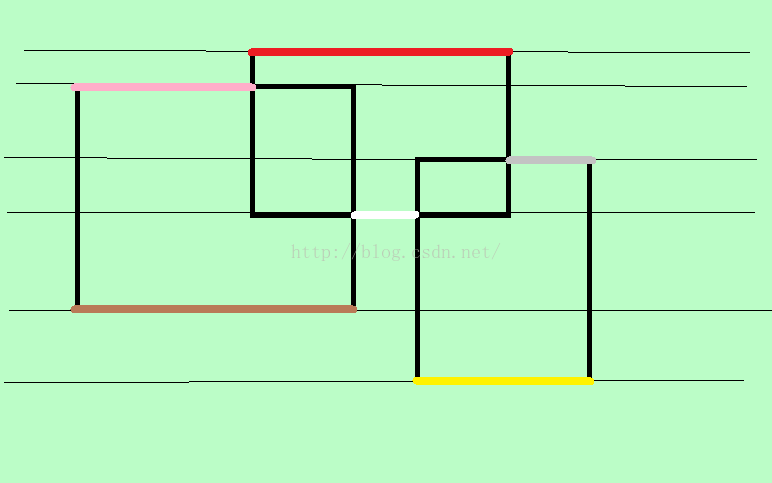
周长可以分成两部分计算,横线和竖线,如图将所有彩色的横线加起来就是横向的所有长度了
然后可以采用竖直方向的扫描线将竖线的所有长度求出来
那么怎么计算横线的长度呢?
横线的长度 = 【现在这次总区间被覆盖的长度和上一次总区间被覆盖的长度之差的绝对值】
这样用自下而上和从左往右的两次扫描即可得到答案。
但是,这样的方法显得有些笨,有没有更高端的方法呢?
再看一张图:
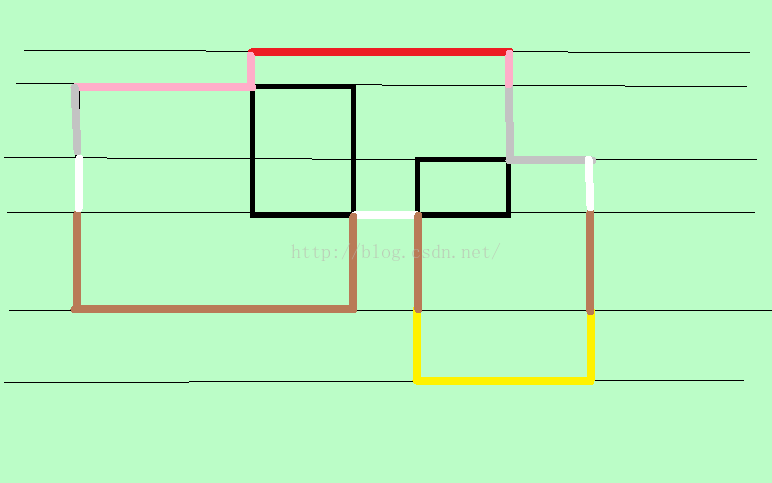
看出什么了吗?这张图在上面那张图的基础上多了几条竖线。
我的意思是说,我们可以只做一次自下而上的扫描就把横线竖线都算出来!
竖线的算法和上面说的方法一样:【现在这次总区间被覆盖的长度和上一次总区间被覆盖的长度之差的绝对值】
竖线要怎么计算?
首先我们现在改一下线段树保存的属性,我们用如下信息记录线段树的节点:
1. l , r : 该节点代表的线段的左右端点坐标
2.len : 这个区间被覆盖的长度(即计算时的有效长度)
3.s : 表示这个区间被覆盖了几次
4. lc , rc : 标记这个节点的左右两个端点是否被覆盖(0表示没有,1表示有)
5.num :这个区间有多少条不连续线段(这个区间被多少条线段覆盖)
这里的num涉及到竖线的计算,故解释一下,举几个例子:
若区间[0,10]被[1,2][4,5]覆盖,则num = 2
若区间[0,10]被[1,3][4,5]覆盖,则num = 1(两区间刚好连在一起)
若区间[0,10]被[1,5][2,6]覆盖,则num = 1(两区间连起来还是一段)
然后就可以计算竖线了:
竖线的长度 = 【下一条即将被扫到的横线的高度 - 现在扫到的横线的高度】2num
乘2是因为每条线段有两个端点;
看上图中棕色线段的竖线有4条,因为棕色的横线由2条线段组成
白色线段的竖线只有2条,因为白色的横线由1条线段组成(虽然这1条线段是由许多线段组合而成,但它依旧只算1条线段)
这样,依旧只扫一次就可以算出周长。
转自:
代码:
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<ctime>
#include<cmath>
#include<string>
#include<cstring>
#include<bitset>
#include<vector>
#include<queue>
#include<stack>
#include<set>
#include<map>
#include<iomanip>
#include<algorithm>
#define IOS ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
#define endl "\n"
#define PI acos(-1)
//CLOCKS_PER_SEC clock()函数每秒执行次数
using namespace std;
const int INF = 0x3f3f3f3f;
const int N = 2e4+5;
int mod = 1e9 +7;
int n,m,k,S,T;
struct node{
//lc,rc表示左右端点是否被覆盖
int l,r,len,num,s,lc,rc;
}tr[N * 4];
struct nodes{
int l,r,h,w;
bool operator<(const nodes &t)const{
return h < t.h;
}
}e[N];
void pushup(int u){
if(tr[u].s){
tr[u].len = tr[u].r - tr[u].l + 1;
tr[u].lc = tr[u].rc = 1;
tr[u].num = 1;
}
else if(tr[u].l == tr[u].r){
tr[u].lc = tr[u].rc = tr[u].len = tr[u].num = 0;
}
else{
tr[u].len = tr[u << 1].len + tr[u << 1 | 1].len;
//左儿子的左端点被覆盖则父节点的左端点被覆盖
tr[u].lc = tr[u << 1].lc;
//右端点同上
tr[u].rc = tr[u << 1 | 1].rc;
//若左儿子的右端点和右端点的左儿子都被覆盖则可以合并一个区间,区间数-1;
tr[u].num = tr[u << 1].num + tr[u << 1 | 1].num - (tr[u << 1].rc & tr[u << 1 | 1].lc);
}
}
void build(int u,int l,int r){
tr[u] = {l,r};
if(l == r) return;
int mid = l + r >> 1;
build(u << 1,l,mid),build(u << 1 | 1,mid + 1,r);
}
void modify(int u,int l,int r,int v){
if(tr[u].l >= l && tr[u].r <= r){
tr[u].s += v;
pushup(u);
return;
}
int mid = tr[u].l + tr[u].r >> 1;
if(l <= mid) modify(u << 1,l,r,v);
if(r > mid) modify(u << 1 | 1,l,r,v);
pushup(u);
}
void solve(){
cin >> n;
int cnt = 0;
int ml = INF,mr = -INF;
for(int i = 1 ; i <= n ; ++i){
int x,y,xx,yy;
cin >> x >> y >> xx >> yy;
ml = min(ml,min(x,xx));
mr = max(mr,max(x,xx));
e[cnt++] = {x,xx,y,1};
e[cnt++] = {x,xx,yy,-1};
}
sort(e,e + cnt);
build(1,ml,mr - 1);
int ans = 0;
int last = 0;
for(int i = 0 ; i < cnt ; ++i){
int l = e[i].l,r = e[i].r,h = e[i].h,w = e[i].w;
modify(1,l,r - 1,w);
ans += abs(tr[1].len - last);
ans += (e[i + 1].h - e[i].h) * tr[1].num * 2;
last = tr[1].len;
}
cout << ans << endl;
}
signed main(){
IOS;
solve();
return 0;
}

