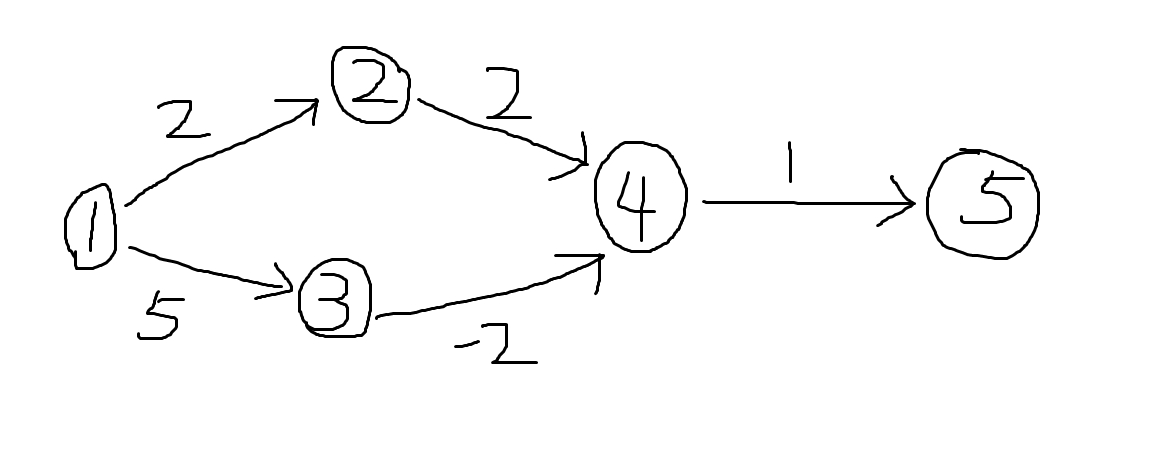
用dijkstra算法解决的的详细步骤
1，初始dist[1] = 0

2，找到了未标识且离源点1最近的结点1，标记1号点，用1号点更新其他所有点的距离，2号点被更新成dist[2] = 2，3号点被
更新成dist[3] = 5

3，找到了未标识且离源点1最近的结点2，标识2号点，用2号点更新其他所有点的距离，4号点被更新成dist[4] = 4

4，找到了未标识且离源点1最近的结点4，标识4号点，用4号点更新其他所有点的距离，5号点被更新成dist[5] = 5

5，找到了未标识且离源点1最近的结点3，标识3号点，用3号点更新其他所有点的距离，4号点被更新成dist[4] = 3

结束
得到1号点到5号点的最短距离是5，对应的路径是1 -> 2 -> 4 -> 5，并不是真正的最短距离

结果：

dijkstra算法在图中走出来的最短路径是1 -> 2 -> 4 -> 5，算出 1 号点到
5 号点的最短距离是2 + 2 + 1 = 5，然而还存在一条路径是1 -> 3 -> 4 -> 5，该路径的长度是5 + (-2) + 1 = 4
因此 dijkstra 算法失效

注：我们可以发现如果有负权边的话4号点经过标记后还可以继续更新
但此时4号点已经被标记过了，所以4号点不能被更新了，只能一条路走到黑
当用负权边更新4号点后5号点距离起点的距离我们可以发现可以进一步缩小成4。  
所以总结下来就是:dijkstra不能解决负权边是因为 dijkstra要求每个点被确定后st[j] = true，dist[j]就是最短距离了
之后就不能再被更新了（一锤子买卖）
而如果有负权边的话，那已经确定的点的dist[j]不一定是最短了