题目描述
有 3030 个篮子,每个篮子里有若干个苹果,篮子里的苹果数序列已经给出。
现在要把苹果分给小朋友们,每个小朋友要么从一个篮子里拿三个苹果,要么从相邻的三个篮子里各拿一个苹果。
苹果可以剩余,而且不同的拿法会导致不同的答案。比如对于序列3 1 3 ,可以分给两个小朋友变成0 1 0;也可以分给一个小朋友变成2 0 2,此时不能继续再分了。所以答案是 22 。
求问对于以下序列,最多分给几个小朋友?
测试数据
7 2 12 5 9 9 8 10 7 10 5 4 5 8 4 4 10 11 3 8 7 8 3 2 1 6 3 9 7 1
算法 DP O(n * $a^4[i]$)
秉承暴力杯的一贯作风,无优化版DP解决此问题 感觉可以优化,但我不会
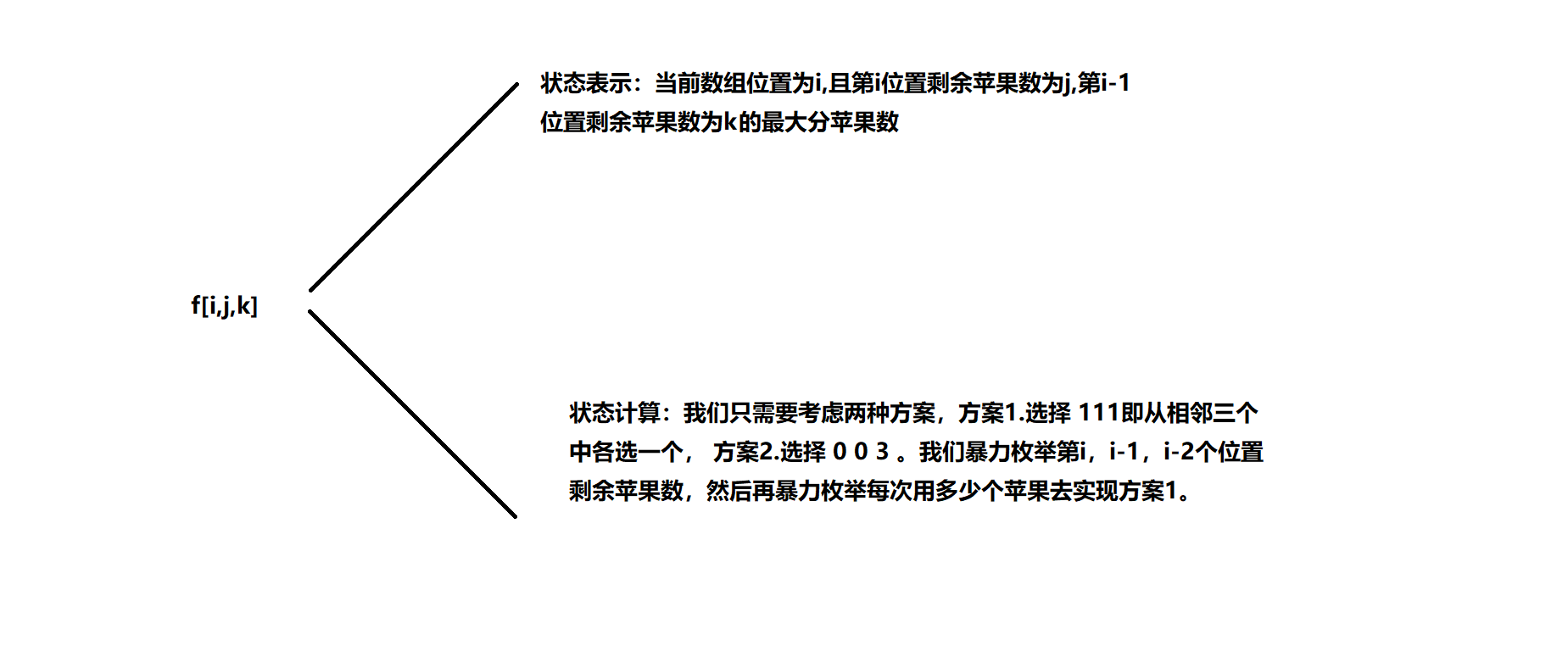
ps:状态表示那里把“剩余”去掉,手残写上去了。
#include <iostream>
#include <cstring>
#include <algorithm>
#include <sstream>
using namespace std;
int a[110];
int f[110][15][15];
int main(){
freopen("data.in","r",stdin);
freopen("data.out","w",stdout);
string line;
getline(cin,line);
stringstream ssin(line);
int n = 1;
while(ssin >> a[n]) n ++;
n -- ;
for(int i=0;i<=a[1];i++)
for(int j=0;j<=a[2];j++)
f[2][i][j] = i / 3 + j / 3;
for(int i=3;i<=n;i++)
{
for(int j=0;j<=a[i - 1];j++)
for(int k=0;k<=a[i];k++)
for(int t=0;t<=a[i-2];t++)
{
int limit = min(min(j,k),t);
for(int cost = 0;cost <= limit;cost++)
{
f[i][j][k] = max(f[i][j][k],f[i - 1][t - cost][j - cost] + cost
+ (k - cost) / 3);
}
}
}
cout << f[n][a[n-1]][a[n]] << endl;
return 0;
}
总结
最后答案是 62,其实我做这题的时候是经历了一定波折的。。。当时是想只用二维来描述这个问题,但实际是不行的。当DP问题已经表示出状态但在状态计算时难以下笔时不如回过头想想自己的状态表示是不是没有表示全面。

