树形DP

$题意：共n个怪兽，每个怪兽的权值是a_i,消灭每个怪兽的花费是与该怪兽直接连接且存活的子节点的权值+a_i$
$你可以使用m次机会，每个机会可以不耗费能量且可以消灭任意一个存活的怪物$
$问你m=0，1，2，3…，n时的最低总能量花费分别为多少。$
比如：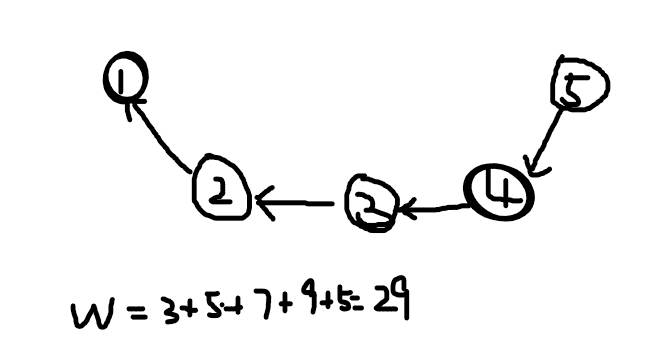

考虑到这里,可以想到f[u][cnt]:以当前结点开始，一共含cnt个节点的集合，但是每个节点有死亡/存活两个状态，所以
$f[1/0][i][j]:表示第i个节点活/死，并且一共含有j个节点的结合$
$初始化：f[0][u][0] = 0, f[1][u][1] = w[u]$

$$状态转移： f[0][u][j+k] = min(f[0][u][j+k], f[0][u][j] + min(f[0][son][k], f[1][son][k]));$$
$$ f[1][u][j+k] = min(f[1][u][j+k], f[1][u][j] + min(f[0][son][k], f[1][son][k] + w[son]));$$
$$当前结点死亡/存活，且共含有j+k个结点，其中j个结点是我自己的的直接子节点，k是我子节点的子节点$$

#include <bits/stdc++.h>

using namespace std;

const int N = 5*1e3 + 10;
typedef long long ll;

ll f[2][N][N];//当前位置删除/没删除，且一共含有n个节点的集合
ll w[N];
int n;
vector<int> g[N];
int siz[N];

void dfs(int u)
{
    siz[u] = 1;
    f[0][u][0] = 0;
    f[1][u][1] = w[u];

    for(auto& v : g[u])
    {
        dfs(v);

        for(int j=siz[u];j>=0;j--)
            for(int k=siz[v];k>=0;k--)
            {
                f[0][u][j+k] = min(f[0][u][j+k], f[0][u][j] + min(f[0][v][k], f[1][v][k]));
                f[1][u][j+k] = min(f[1][u][j+k], f[1][u][j] + min(f[0][v][k], f[1][v][k] + w[v]));
            }

        siz[u] += siz[v];//每次和v这个儿子合并完，size就要加上v的size
    }

}

int main()
{
    int T;cin >> T;
    while(T--)
    {
        int n;
        scanf("%d",&n);

        for(int i=0;i<=n;i++) g[i].clear();

        for(int i=0;i<=n;i++)
            for(int j=0;j<=n;j++)
                f[1][i][j] = f[0][i][j] = 1ll*1e18;

        for(int i=2;i<=n;i++)
        {
            int u;
            scanf("%d",&u);
            g[u].push_back(i);
        }

        for(int i=1;i<=n;i++) scanf("%lld",w+i);
        dfs(1);

        for(int i=n;i>=0;i--) printf("%lld ",min(f[1][1][i], f[0][1][i]));
        puts("");
    }
}