问题

列车从出发地到目的地要经历多个车站。给定相邻车站之间的距离和总时间限制，求能准时到达的最小正整数时速。

注意，车站的发车时刻必须是整点，比如2:30到某个车站，也必须等到3:00才能发车。生成的测试用例保证答案不超过 1e7 ，且 hour 的 小数点后最多存在两位数字 。

输入：dist = [1,3,2], hour = 6
输出：1
解释：速度为 1 时：
- 第 1 趟列车运行需要 1/1 = 1 小时。
- 由于是在整数时间到达，可以立即换乘在第 1 小时发车的列车。第 2 趟列车运行需要 3/1 = 3 小时。
- 由于是在整数时间到达，可以立即换乘在第 4 小时发车的列车。第 3 趟列车运行需要 2/1 = 2 小时。
- 你将会恰好在第 6 小时到达。

输入：dist = [1,3,2], hour = 2.7
输出：3
解释：速度为 3 时：
- 第 1 趟列车运行需要 1/3 = 0.33333 小时。
- 由于不是在整数时间到达，故需要等待至第 1 小时才能搭乘列车。第 2 趟列车运行需要 3/3 = 1 小时。
- 由于是在整数时间到达，可以立即换乘在第 2 小时发车的列车。第 3 趟列车运行需要 2/3 = 0.66667 小时。
- 你将会在第 2.66667 小时到达。

输入：dist = [1,3,2], hour = 1.9
输出：-1
解释：不可能准时到达，因为第 3 趟列车最早是在第 2 小时发车。

算法：二分

我们用ceil()表示上取整，车站之间的距离为si, 车速为v, 则题目要求满足：

ceil(s0/v)+ceil(s1/v)+…+sn-1/v <= hour

而且题目提示时速为最小正整数，且不超过1e7。在一定的范围内，寻找某个满足条件的答案，很容易想到二分：在1到2e7内二分，如果最终答案等于2e7则无解；反之则有解，输出答案即可。

代码

先来一份错误代码：

class Solution {
public:
    bool check(int v, vector<int>& dist, double hour){

        for(int i = 0; i < dist.size()-1; i ++){
            hour -= (dist[i]+v-1)/v;
            if(hour<0) return false;
        }
        hour -= (double)dist.back()/v;
        cout<<v<<' '<<hour<<endl; // 测试样例：[1,1,100000] 2.01
                                  // 10000000 -2.13371e-16 
                                  // 15000000 0.00333333
                                  // ...      ...
        return hour >= 0; 
    }
    int minSpeedOnTime(vector<int>& dist, double hour) {
        int l = 1, r = 2e7;
        while(l < r){
            int mid = l + r >> 1;
            if(check(mid,dist,hour)) r = mid;
            else l = mid + 1;
        }
        if(r == 2e7) return -1;
        return r;
    }
};

上面这份代码在二分判断的时候，用hour一直减每一段需要的时间，再与0作比较，逻辑上没有问题，但错就错在用浮点数与0作比较。我们知道浮点数在计算机内部的表示是用的IEEE浮点数表示法，表示的值是离散且不均匀的：

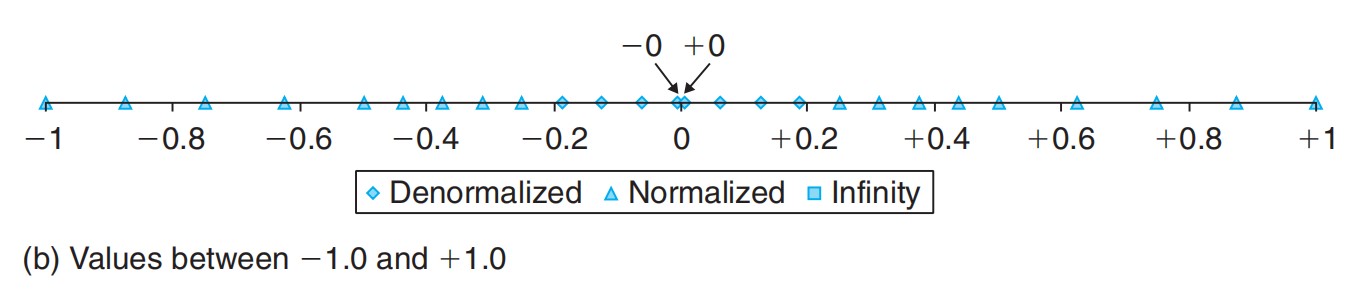
也就是说，浮点数不能完全精确的表示某些数值，导致在运算的过程中会有精度损失，最后得到的数不一定是真正的0！！

比如当我们输入如51行注释所示的样例会出错。打印出速度和剩余时间，可以看出，虽然在该速度下，减去最后一段所需时间后，剩余时间本应该恰好为0（在IEEE浮点表示法中为全0），但却是一个很小的负数，这就是因为在减的过程中出现了精度损失，最后得到的数不是真正的全0，而是一个负数！

更直观的解释：你可以在浏览器中按F12，点击Console, 输入0.2+0.4看看结果。原因在于0.2和0.4都不能被精确的用浮点数表示，都是做了舍入的，所以结果会不正确。

解决这个问题的方式有两种：
1. 既然有精度损失，我们就不拿这个数直接与0做比较，而用这个数的绝对值与一个很接近0的正数作比较即可: fabs(hour) <= 0.00000000001f. 但是在本题中，除了等于0，大于0也是可以的，这样就要做两次判断
2. 不要用hour做减法与0作比较，因为在接近0的地方浮点数很容易丢失精度。所以我们用一个新的变量res做加法与hour作比较，这样就不会出错。比如下面的代码

正确的代码：

class Solution {
public:
    bool check(int v, vector<int>& dist, double hour){
        double res = 0;
        for(int i = 0; i < dist.size()-1; i ++){
            res += (dist[i]+v-1)/v;
        }
        res += (double)dist.back()/v;
        cout<<res<<' '<<hour<<endl;
        return res <= hour; 
    }
    int minSpeedOnTime(vector<int>& dist, double hour) {
        int l = 1, r = 2e7;
        while(l < r){
            int mid = l + r >> 1;
            if(check(mid,dist,hour)) r = mid;
            else l = mid + 1;
        }
        if(r == 2e7) return -1;
        return r;
    }
};

所以，下次遇到浮点数的比较，切记不要直接作=/!=的判断，而要尽量（可能需要引入一个很小的值epsilon）使用<=/>=判断。

当然，正规的题目涉及到浮点数，会允许结果有误差，但是一定要知道原因，避免遇到不允许误差的情况却不知道怎么办！