约瑟夫问题

作者： 作者的头像   你好世界wxx ,  2021-05-30 21:56:02 ,  所有人可见 ,  阅读 814

18


22

约瑟夫问题

这个问题是以弗拉维奥·约瑟夫命名的，他是1世纪的一名犹太历史学家。他在自己的日记中写道，他和他的40个战友被罗马军队包围在洞中。他们讨论是自杀还是被俘，最终决定自杀，并以抽签的方式决定谁杀掉谁。约瑟夫斯和另外一个人是最后两个留下的人。约瑟夫斯说服了那个人，他们将向罗马军队投降，不再自杀。约瑟夫斯把他的存活归因于运气或天意，他不知道是哪一个。 —— 【约瑟夫问题】维基百科

本文会探讨约瑟夫问题的各种解法。

参考网址：剑指 Offer 62 题解、约瑟夫环、今日头条2018春招研发岗笔试

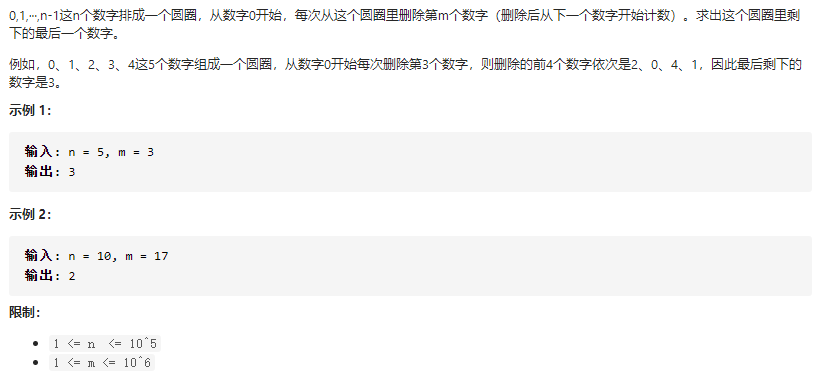
一. 基本约瑟夫问题

image-20210530194044730.png

一. 模拟

分析

  • 将0~n-1存放到容器中（C++存放到vector中，Java存放到ArrayList中），每次从数组中删除一个元素，直到容器中只剩下一个元素，这个元素就是答案。

  • 这种做法的时间复杂度是$O(n ^ 2)$，因为每次都会改变容器的大小，牵涉到数组的迁移。很可能超时。

代码

  • C++
// TLE
class Solution {
public:
    int lastRemaining(int n, int m) {
        vector<int> f(n);
        for (int i = 0; i < n; i++) f[i] = i;
        int index = 0;  // 每次需要删除的人的下标
        while (n > 1) {
            index = (index + m - 1) % n;
            f.erase(f.begin() + index);
            n--;
        }
        return f[0];
    }
};
  • Java
/**
 * 执行用时：1114 ms, 在所有 Java 提交中击败了7.09%的用户
 * 内存消耗：40.6 MB, 在所有 Java 提交中击败了9.73%的用户
 */
class Solution {
    public int lastRemaining(int n, int m) {
        List<Integer> f = new ArrayList<>(n);
        for (int i = 0; i < n; i++) f.add(i);
        int index = 0;
        while (n > 1) {
            index = (index + m - 1) % n;
            f.remove(index);
            n--;
        }
        return f.get(0);
    }
}

二. 递推

分析

  • 所谓递推就是从前一个状态递推下一个状态。

  • 定义状态f(n, m)：表示0~n-1这n个人围成一圈，每m个人删除一个人，最后的答案是f(n, m)。分析如下：

image-20210530200553493.png

  • 我们可以使用递归实现（C++演示），也可以使用递推实现（Java演示）。

  • 注意，我们的边界是最后只有一个人，编号为0。

  • 该做法时间复杂度是$O(n)$的。

代码

  • C++
class Solution {
public:
    int lastRemaining(int n, int m) {
        if (n == 1) return 0;
        return (lastRemaining(n - 1, m) + m) % n;
    }
};
  • Java
/**
 * 执行用时：7 ms, 在所有 Java 提交中击败了99.88%的用户
 * 内存消耗：35.1 MB, 在所有 Java 提交中击败了91.17%的用户
 */
class Solution {
    public int lastRemaining(int n, int m) {
        int res = 0;
        // f(n) = (f(n - 1) + m) % n, 边界f(2) = (f(1) + m) % 2, 因此从2开始循环
        for (int i = 2; i <= n; i++) res = (res + m) % i;
        return res;
    }
}

三. 递推法加速

分析

  • 上面的做法是线性的，但是我们考虑如果n非常大，比如$n < 10 ^ {12}$，但是m不是很大，比如$m \le 1000$，这个时候这种方法就会超时了。需要优化。

  • 上述递推做法的递推式是：$f(n) = (f(n - 1) + m) \% n$，因为n很大，我们需要加很多次m后才会对n取模，于是我们考虑一次增加很多个m，例如t个，则递推式变为了：

$$ f(n + t - 1) = (f(n - 1) + t \times m) \% (n + t - 1) $$

  • 假设加了t次之后才产生余数，那么就有$f(n - 1) + tm \ge n + t - 1$，即：

$$ t \ge \frac{n - f(n - 1) - 1}{m-1} $$

  • 每次t都取上式的上取整。

  • 注意，如果我们在递推的最后，发现计算得到的t满足i-1+t>n，则说明不需要取余了，直接返回res + (n - i + 1) * m即可。

代码

  • C++
// 15ms
class Solution {
public:
    int lastRemaining(int n, int m) {
        if (m == 1) return n - 1;  // 后面m-1会做分母
        int res = 0;
        for (int i = 2, t = 0; i <= n; i += t) {
            t = (i - res + m - 3) / (m - 1);
            if (i + t - 1 > n) return res + (n - i + 1) * m;
            res = (res + t * m) % (i + t - 1);
        }
        return res;
    }
};
  • Java
//
class Solution {
    public int lastRemaining(int n, int m) {
        if (m == 1) return n - 1;  // 后面m-1会做分母
        int res = 0;
        for (int i = 2, t = 0; i <= n; i += t) {
            t = (i - res + m - 3) / (m - 1);
            if (i + t - 1 > n) return res + (n - i + 1) * m;
            res = (res + t * m) % (i + t - 1);
        }
        return res;
    }
}

二. 拓展问题

Leetcode 0390 消除游戏

题目描述：Leetcode 0390 消除游戏

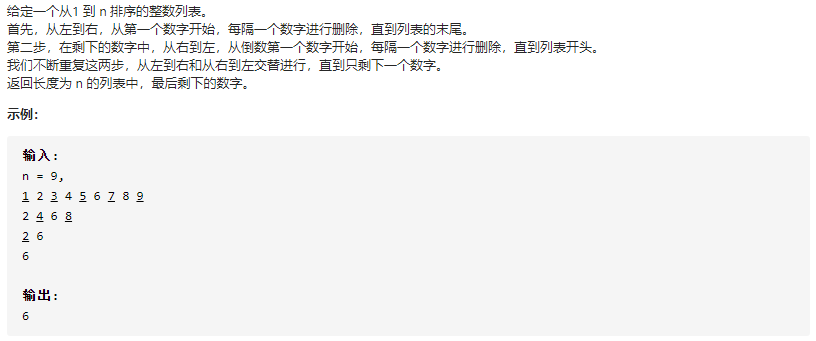
image-20210530210335172.png

分析

  • 本题的考点：约瑟夫问题。

  • 假设一共n个数据，如果从左测开始删除最终剩余的数记为f(n)，从右侧开始删除最终剩余的数记为g(n)。

  • 求f(n)的第一趟(1~n中删除所有奇数)：2 4 6 8 … 。将2 4 6 8 ...重新编号为1 2 3 4 ...。

  • 则第二趟从右向左删除得到的数据为g(n/2)，所以有f(n)= $2 \times g(n/2)$ ①

  • 因为f(n)和g(n)的求解是对称的，所以可以得到：f(n)+g(n)=n+1 ②

  • 结合①②，可知f(n) = 2g(n/2) = 2 * (n / 2 + 1 - f(n/2))

代码

  • C++
class Solution {
public:
    int lastRemaining(int n) {
        if (n == 1) return 1;
        return 2 * (n / 2 + 1 - lastRemaining(n / 2));
    }
};
  • Java
class Solution {
    public int lastRemaining(int n) {
        if (n == 1) return 1;
        return 2 * (n / 2 + 1 - lastRemaining(n / 2));
    }
}

时空复杂度分析

  • 时间复杂度：$O(log(n))$。

  • 空间复杂度：$O(log(n))$。

AcWing 1455. 招聘

问题描述

image-20210530210833308.png

分析

  • 本题的考点：约瑟夫问题。

  • 本题也可以使用递推解决。

  • 定义状态f(n, k)：表示0~n-1这n个人围成一圈，从第k个数A[k]开始用，最终剩余的编号是多少。

  • 分析如下：

image-20210530212656830.png

  • 这里的递归写法会超时，如下也给出了递归写法。

  • 另外可以采用非递归写法，当只有一个人时，答案res = 0，我们从两个人开始递推，这里需要注意我们的真实操作从n个人变为n-1个人用的是a[0]，从n-1个人变为n-2个人我们用的是a[1]，则从2个人变为1个人我们用的是a[(n-2)%m]，因此我们这里的k需要从(n-2)%m开始，每次k--（因为我们的操作是反的，相当于每次添加一个人）。

代码

  • C++
// 超时TLE
#include <iostream>

using namespace std;

const int N = 1010;

int n, m;
int a[N];

int dp(int n, int k) {
    if (n == 1) return 0;
    return (dp(n - 1, (k + 1) % m) + a[k]) % n;
}

int main() {

    int T;
    scanf("%d", &T);

    while (T--) {
        scanf("%d%d", &n, &m);
        for (int i = 0; i < m; i++) scanf("%d", &a[i]);
        printf("%d\n", dp(n, 0));
    }

    return 0;
}

// 通过
#include <iostream>

using namespace std;

const int N = 1010;

int n, m;
int a[N];

int main() {

    int T;
    scanf("%d", &T);

    while (T--) {
        scanf("%d%d", &n, &m);
        for (int i = 0; i < m; i++) scanf("%d", &a[i]);
        int res = 0;
        for (int i = 2, k = (n - 2) % m; i <= n; i++, k = (k - 1 + m) % m)
            res = (res + a[k]) % i;
        // 上面的循环也可以写为：
        /**
        for (int i = 2; i <= n; i++)
            res = (res + a[((n - i) % m + m) % m]) % i;
        */
        printf("%d\n", res);
    }

    return 0;
}

2 评论

用户头像
ben380   2022-09-25 19:34         踩      回复

tql

用户头像
王同学.   2022-04-19 00:12         踩      回复

佬，加速递推里面的 t = (i - res + m - 3) / (m - 1); 是怎么得到的啊