各种排序
各个排序的空间,时间复杂度,以及稳定性如下
| 排序方法 | 时间复杂度(平均) | 时间复杂度(最坏) | 时间复杂度(最好) | 空间复杂度 | 稳定性 | 复杂性 |
|---|---|---|---|---|---|---|
| 直接插入排序 | O(n^2) | O(n^2) | O(n) | O(1) | 稳定 | 简单 |
| 希尔排序 | O(nlog_2n) | O(n^2) | O(n) | O(1) | 不稳定 | 较复杂 |
| 直接选择排序 | O(n^2) | O(n^2) | O(n^2) | O(1) | 不稳定 | 简单 |
| 堆排序 | O(nlog_2n) | O(nlog_2n) | O(nlog_2n) | O(1) | 不稳定 | 较复杂 |
| 冒泡排序 | O(n^2) | O(n^2) | O(n) | O(1) | 稳定 | 简单 |
| 快速排序 | O(nlog_2n) | O(n^2) | O(nlog_2n) | O(nlog_2n) | 不稳定 | 较复杂 |
| 归并排序 | O(nlog_2n) | O(nlog_2n) | O(nlog_2n) | O(n) | 稳定 | 较复杂 |
快速排序
快排的设计思想
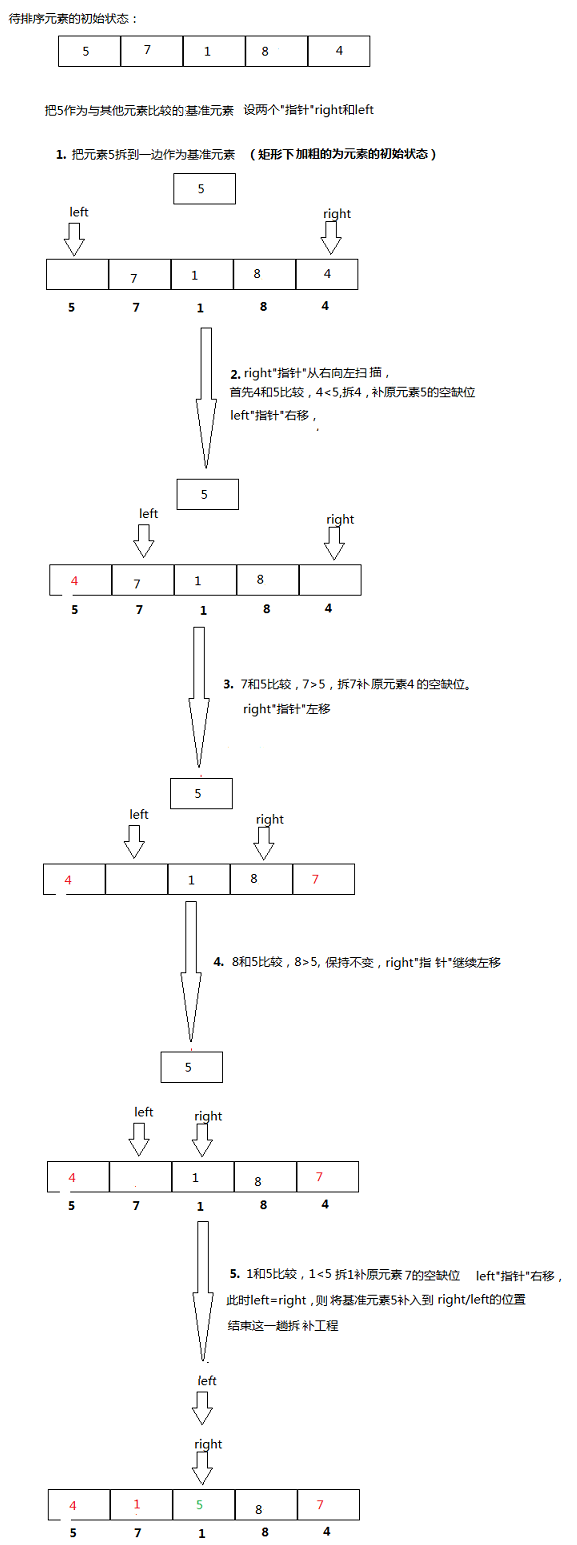
设计代码
递归版
void Quick_Sort(int *arr,int l,int r){
if(l>=r)return;
int val=arr[l];
int i=l-1,j=r+1;
while(i<j){
do i++; while(val>arr[i]);
do j--; while(val<arr[j]);
if(i<j) swap(arr[i],arr[j]);
}
//左半部分开始遍历
Quick_Sort(arr,l,j);
//右半部分开始遍历
Quick_Sort(arr,j+1,r);
}
非递归版的
void Quick_Sort(int *arr,int l,int r){
//先存大再存小,取得时候就可以先取小再取大,大小是指的是数组的索引值
stack<int> lowHight;
lowHight.push(r);
lowHight.push(l);
while(!lowHight.empty()){
int i=lowHight.top();
lowHight.pop();
int j=lowHight.top();
lowHight.pop();
if(i>=j)continue;
int val=a[l];
while(i<j){
while(i<j&&val<arr[j])
j--;
swap(arr[j],arr[i]);
while(i<j&&val>arr[i])
i++;
swap(arr[i],arr[j]);
}
//栈的先进后出特性,先处理左边的数据
//右边
lowHight.push(r);
lowHight.push(i+1);
//左边
lowHight.push(i-1);
lowHight.push(l);
}
}
梳排序
梳排序是冒泡排序的一种改进方式,为此先把冒泡排序写上来,两者互相对比
冒泡排序
void Buddle_Sort(int *arr,int l,int r){
if(l>=r)return;
for(int i=l;i<r;i++){
for(int j=i;j<r-i;j++){
if(arr[j]>arr[j+1])
swap(arr[j],arr[j+1]);
}
}
}
梳排序
原理:通过将数组分为小的数组,来达到降低时间复杂度的目的
交换案例
假设待数组[8 4 3 7 6 5 2 1]
待排数组长度为8,而8÷1.3=6,则比较8和2,4和1,并做交换
[8 4 3 7 6 5 2 1]
[8 4 3 7 6 5 2 1]
交换后的结果为
[2 1 3 7 6 5 8 4]
第二次循环,更新间距为6÷1.3=4,比较2和6,1和5,3和8,7和4
[2 1 3 7 6 5 8 4]
[2 1 3 7 6 5 8 4]
[2 1 3 7 6 5 8 4]
[2 1 3 7 6 5 8 4]
只有7和4需要交换,交换后的结果为
[2 1 3 4 6 5 8 7]
第三次循环,更新距离为3,没有交换
第四次循环,更新距离为2,没有交换
第五次循环,更新距离为1,三处交换
[2 1 3 4 6 5 8 7]
[2 1 3 4 6 5 8 7]
[2 1 3 4 6 5 8 7]
三处交换后的结果为[1 2 3 4 5 6 7 8]
交换后排序结束,顺序输出即可得到[1 2 3 4 5 6 7 8]
void Comb_Sort(int *arr,int l,int r){
float factor=1.3;
int g=r-l;
//n the size of array
int n=r-l;
bool flag=true;
while(g>1||flag){
g=(g>1)?g/factor:g;
flag=false;
int i=0;
//如果全都排序好了,flag为false,g=1直接跳出循环。
while(i+g<n){
if(arr[i]>arr[g+i]){
std::swap(arr[i],arr[g+i]);
flag=true;
}
i=i+1;
}
}
}
归并排序
分而治之
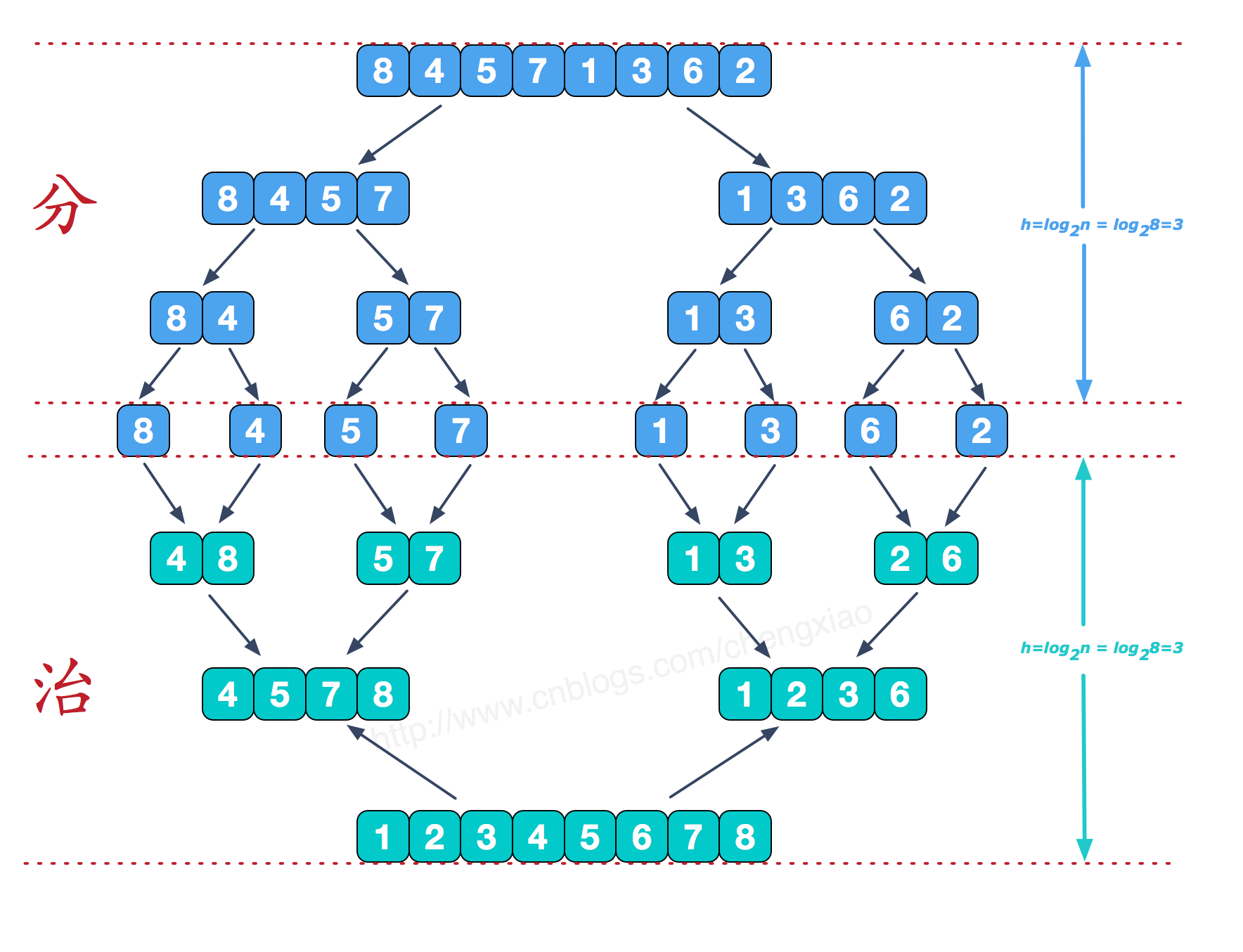
合并有序子序列
void merge(vector<int> nums,int l,int r){
if(l>=r)return;
int mid=l+r>>1;
merge(nums,l,mid);
merge(nums,mid+1,r);
vector<int> tem;
int i=l,j=mid+1;
while(i<=mid&&j<=r){
if(nums[i]<=nums[j])tem.push_back(nums[i++]);
else tem.push_back(nums[j++]);
}
while(i<=mid)tem.push_back(nums[i++]);
while(j<=r)tem.push_back(nums[j++]);
i=l;
for(auto t:tem){
nums[i++]=t;
}
}
堆排序
void adjust_heap(vector<int>& nums,int x,int n){
int l=x*2+1;
int r=x*2+2;
int max=x;
if(l<n&&nums[l]>nums[max])max=l;
if(r<n&&nums[r]>nums[max])max=r;
if(max!=x){
swap(nums[max],nums[x]);
adjust_heap(nums,max,n);
}
}
void heap_sort(vector<int>& nums){
int n=nums.size();
for(int i=n/2-1;i>=0;i--){
adjust_heap(nums,i,n);
}
for(int i=n-1;i>=0;i--){
swap(nums[i],nums[0]);
adjust_heap(nums,0,i);
}
}
插入排序
直接插入排序
时间复杂度:O(n^2)
具体过程可以参考此图片

void DistrictInsertSort(int A[],int n){
int i,j;
for(i=1;i<n;i++){
if(A[i]<A[i-1]){
int temp=A[i];
for(j=i-1;j>=0&&temp<A[j];--j){
A[j+1]=A[j];
}
A[j+1]=temp;
}
}
}
希尔排序
希尔交换排序
void ShellSort(int A[],int n){
//前后记录位置的增量 dk
//增量dk 并逐步减小增量
for(int dk=n/2;dk>0;dk/=2){
//从第dk个元素,逐个对其所在组进行直接插入排序操作
for(int i=dk;i<n;++i){
int j=i;
while(j-dk>=0&&A[j]<A[j-dk]){
//插入排序交换法
swap(A[j],A[j-dk]);
j-=dk;
}
}
}
}
希尔插入(移动)排序
void ShellSort(int *A,int n){
for(int dk=n/2;dk>0;dk/=2){
for(int i=dk;i<n;i++){
int j=i;
int temp=A[i];
if(A[j]<A[j-dk]){
while(j-dk>=0&&temp<A[j-dk]){
//移动法
A[j]=A[j-dk];
j-=dk;
}
A[j]=temp;
}
}
}
}
折半插入排序
直接插入排序的改进版,时间复杂度为O(n^2)
void InsertSort(int A[],int n){
int i,j=0;
for(i=1;i<n;i++){
int temp=A[i];
low=1;
high=i-1;
while(low<high){
mid=(low+high)/2;
if(A[mid]>temp){
high=mid-1;//查找左半子树
}
else
low=mid+1;
for(j=i-1;j>high+1;--j){
A[j+1]=A[j];
}
A[high+1]=temp;
}
}
}


折半插入for循环应该在while循环之外吧
梳子函数内部改成n=r+1好像就正常了。
合并排序的vector[HTML_REMOVED]nums 参数应该是引用。梳子排序无法使用,谢谢
棒棒哒!
哪里有不对的请多多指正