(一) 题目传送门

什么是前缀和?
原数组: $a[1], a[2], a[3], a[4], a[5], …, a[n]$
前缀和 $S_{i}$为数组的前$i$项和
前缀和: $S[i] = \sum_{k=1}^{i}{a_{k}}$
注意：为避免边界情况，前缀的下标统一从1开始

前缀和的作用？
快速求出一段连续区间的和
例如求区间$[l,r]$的和，就应该是$S_{r}-S_{l-1}$

#include <iostream>

using namespace std;

const int N = 100010;

int a[N];

int main()
{
    int n , q;
    cin >> n >> q;
    for(int i = 1 ; i <= n ; i++ ) 
    {
        int x;
        cin >> x;
        a[i] = a[i - 1] + x;
    }



    while(q--)
    {
        int l , r;
        cin >> l >> r;
        cout << a[r] - a[l - 1] << endl;
    }
    return 0;
}

(二) 题目传送门

将一维前缀和推广向二维，那么$s[i][j]$就表示以一个矩阵的和，且$(1,1)$为矩形左上角，$(i,j)$为矩阵右下角

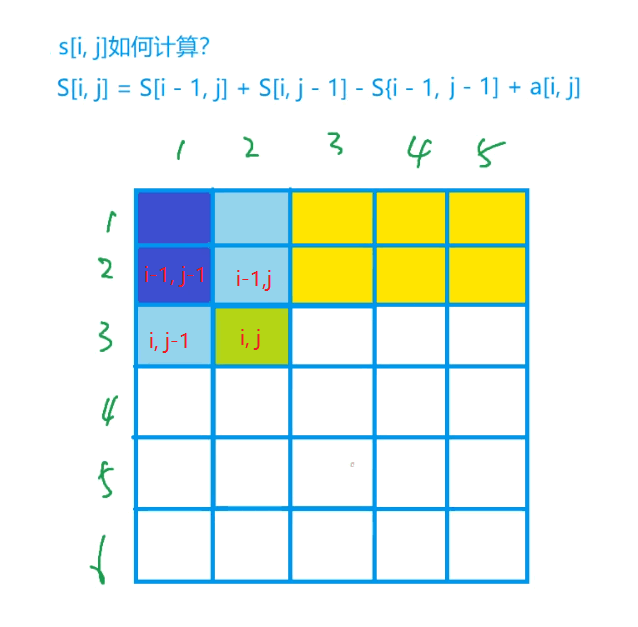
如何计算$s[i][j]$？
如下图所示，通过两个矩阵的和相加减掉重复矩阵再加上$(i,j)$原来的值，就可以计算出$s[i][j]$；
不难发现$s[i-1][j]$、$s[i][j-1]$、$s[i-1][j-1]$已经在计算$s[i][j]$之前已经被计算过了。

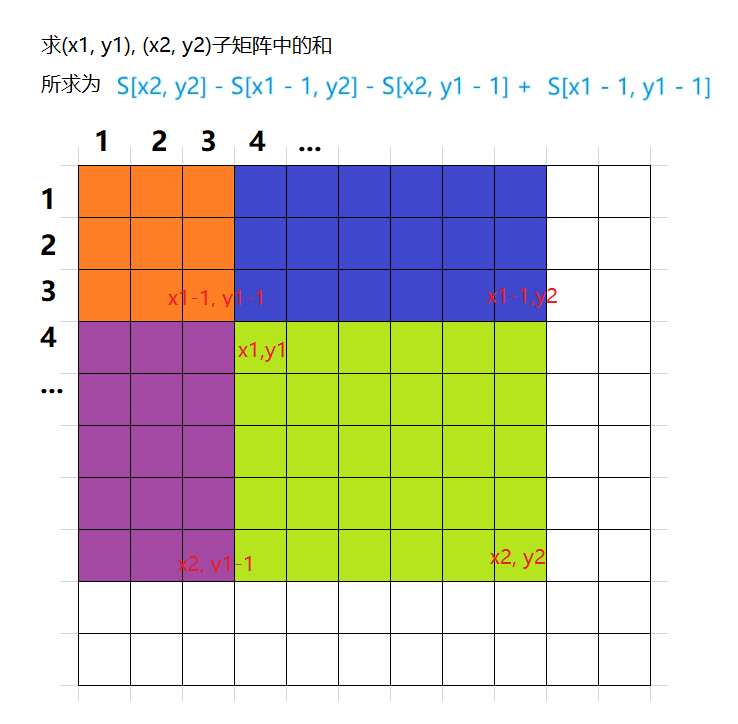
如何通过矩阵前缀和来求得一个矩阵的和？
如下图所示，因为起点都是$(1,1)$，所以可以用一个大矩阵，减掉两个小矩阵，再加回一个重复减掉的小矩阵即可

#include <iostream>

using namespace std;

const int N = 1010;

int a[N][N] , n , m , q;

int main()
{
    cin >> n >> m >> q;

    for(int i = 1 ; i <= n ; i++)
        for(int j = 1 ; j <= m ; j ++)
        {
            cin >> a[i][j];
            a[i][j] += a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1];
        }

    while(q--)
    {
        int x1 , y1 , x2  ,y2;
        cin >> x1 >> y1 >> x2 >> y2;
        cout << a[x2][y2] - a[x2][y1 - 1] - a[x1 - 1][y2] + a[x1 - 1][y1 - 1] << endl;
    }
}

(三) 题目传送门

什么是差分？
首先给定一个原数组$a：a[1], a[2], a[3],,,,,, a[n]$;
然后我们构造一个数组$b ： b[1] ,b[2] , b[3],,,,,, b[i]$;
使得 $a[i] = b[1] + b[2 ]+ b[3] +,,,,,, + b[i]$
也就是说，$a$数组是$b$数组的前缀和数组，反过来我们把$b$数组叫做$a$数组的差分数组。换句话说，每一个$a[i]$都是$b$数组中从头开始的一段区间和。

如何构造差分数组？
最直接的方法如下：
a[0 ]= 0;

b[1] = a[1] - a[0];

b[2] = a[2] - a[1];

b[3] =a [3] - a[2];

........

b[n] = a[n] - a[n-1];

我们只要有$b$数组，通过前缀和运算，就可以在$O(n)$ 的时间内得到$a$数组。

那么如何用差分解决这道区间修改的问题呢？
我们可以进行如下操作：
1、先将$b[l]$加上$c$，此时再计算$a$数组，应该是如下：$a[1]、a[2]、a[3]、…、a[l]+c、a[l+1]+c、…a[r+1]、a[r+1]、…a[n]+c$
2、显然此时还是不够的，因为从$r+1$开始，之后的一段区间是没必要$+c$的，因此我们只需要将$a[r+1]$减$c$即可

#include <iostream>

using namespace std;

const int N = 100010;

int n , m , a[N] , b[N];

int main()
{
    cin >> n >> m;

    for(int i = 1 ; i <= n ; i++)    
    {
        cin >> a[i];
        b[i] = a[i] - a[i - 1];
    }

    while(m--)
    {
        int l , r , c;
        cin >> l >> r >> c;
        b[l] += c , b[r + 1] -= c;
    }

    //b数组的前缀和数组就是原数组
    for(int i = 1 ; i <= n ; i++)
    {
        b[i] += b[i - 1];
        cout << b[i] << ' ';
    }
}

(四) 题目传送门
有了一维差分的基础，我们知道差分数组的前缀和数组就是原数组，因此我们只需要将差分操作记录下来既可以，然后通过差分矩阵还原出原矩阵即可。

#include <iostream>

using namespace std;

const int N = 1010;

int a[N][N];
int n , m, q;

//以(i,j)右下方的点，在计算前缀和时都会累加上a[i][j]，
//因此如果想给以(x1,y1)为左上角，以(x2,y2)为右下角的矩阵加上c这个差分值，
//需要进行如下操作，这样可既不多加也不少加
//类似于矩阵前缀和，需要把握每个点影响的都是它右下方的点这个思想
void insert(int x1 , int y1 , int x2 , int y2 , int c)
{
    a[x1][y1] += c;
    a[x1][y2 + 1] -= c;
    a[x2 + 1][y1] -= c;
    a[x2 + 1][y2 + 1] += c;
}

int main()
{
    cin >>n >> m >> q;

    for(int i =  1; i <= n ; i++)
        for(int j =1  ; j <= m ; j++)
        {
            int x;
            cin >> x;
            insert(i , j , i , j , x);//原数组的(i,j)上是x，相当于在(i,j)到(i,j)这个矩阵范围里加上x
        }

    while(q--)
    {
        int x1 , x2 , y1 , y2 , c;
        cin >> x1 >> y1 >> x2 >> y2 >> c;
        insert(x1 , y1 , x2 , y2 , c);
    }

    for(int i = 1 ; i <= n ; i++)
    {
        for(int j = 1 ; j <= m ; j++)
        {
            a[i][j] += a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1];
            cout << a[i][j] << ' ';
        }
        cout << endl;
    }
    return 0;
}