树状数组

• 功能: 支持快速单点修改 + 区间查询 O(logn)

• 分析:

  对于任意长度的数组, 其长度(设为x)都可以表示为二进制写法:

  $$ x = 2^{ik} + 2^{ik-1} + … + 2^{i1} ({ik} > {ik-1} > … > {i1}, k <= logx) $$

  现将这个长度为x的数组分成k个部分:
  (x - 2^i1, x] (长度为2^i1)
  (x - 2^i1 - 2^i2, x - 2^i1] (长度为2^i2)
  …
  (0, x - 2^i1 - 2^i2, x - 2^i1 - … - 2^ik-1] (长度为2^ik)

  设C(R)为区间[R - lowbit(R) + 1, R]范围内的和; (也就是右端点为R的, 长度为lowbit(R)的区间和)
  C(i)所对应的区间和如图所示(以16项为例):
  

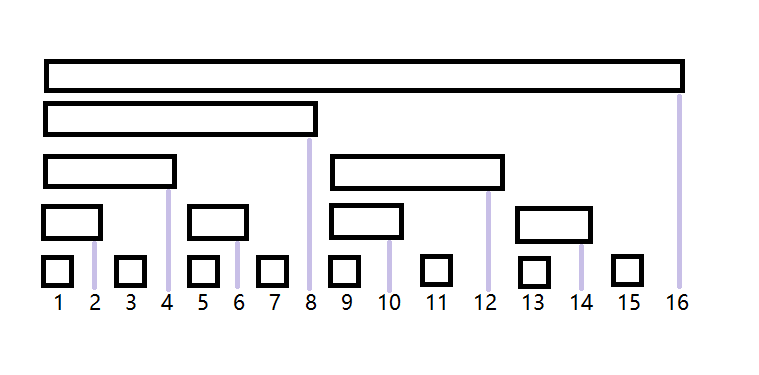
  那么对于任意一个C(i), 它代表的和由哪些孩子节点组成呢? (了解这个可以用来区间查询)

  首先C(i)一定包含位置i本身, 则剩余范围还剩[i - lowbit(i) + 1, i - 1];
  对于任意的正整数i, i一定可以表示为 …10..0(末尾假设有k个0)的写法;
  则i - 1可以表示为…01…1(末尾有k个1);
  因此, i - 1一定可以分成k段来求:
  1. (…01..10, …01…1]
  2. (…01.100, …01..10]
  ....
  k. (…00…0, …010..0]
  这些区间的和又分别可以对应一个C(a)的值(a为上面各区间的右端点);

  图示:
  

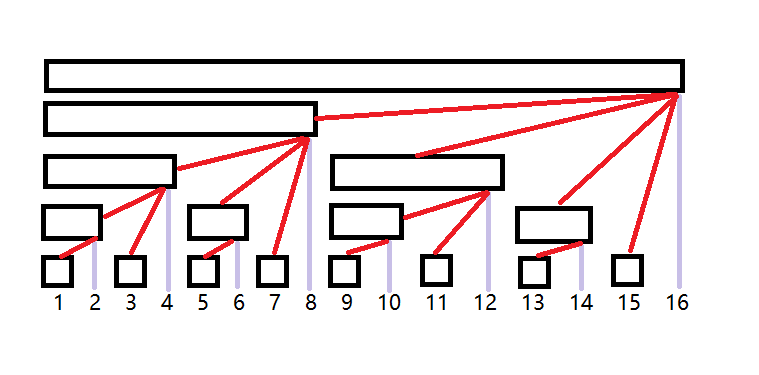
  对于任意一个位置i, 如何求出在树状数组中那些节点区间包含了位置i呢?(了解这个用来单点修改)

  由对之前的分析可得, 对于任意表示为…10…0(末尾有k个0)的父节点;
  它的子节点一定表示为…01..10..0(后面任意个1和任意个0, 但是末尾1和0的个数加起来是k);
  因此可以由子节点(设为v)增加lowbit(v)后, 逆推父节点;

• 结论:

  修改操作(add(x, c)): a[x] += c;

  for(int i = x;i <= n;i += lowbit(i)) tr[i] += c;
  

  查询操作(sum(x)): 查询[1, x]

  for(int i = x;i;i -= lowbit(i)) res += tr[i];
  

  对于任意区间[l, r], 其区间和为sum(r) - sum(l - 1);
  将差分数组和树状数组结合, 可以实现快速区间修改和单点查询操作(O(logn))