输出所有的形如aabb的四位完全平方数(7744问题)

做法1

#include <iostream>
#include <cmath>

using namespace std;

int main() {
    for (int a = 1; a <= 9; a ++ )

        for (int b = 0; b <= 9; b ++ ) {

            int n = a * 1100 + b * 11;   // aabb
            int m = floor(sqrt(n) + 0.5);

            if (m * m == n)
                cout << n << endl;
        }

    return 0;
}

做法2

#include <iostream>
#include <cmath>

using namespace std;

int main() {
    for (int x = 1; ; x ++ ) {

        int n = x * x;

        if (n < 1000)
            continue;

        if (n > 9999)
            break;
        int a = n / 100;
        int b = n % 100;

        if (a / 10 == a % 10 && b / 10 == b % 10)
            cout << n << endl;
    }

    return 0;
}

总结

如何判断一个数n是否是完全平方数？
m = floor(sqrt(n) + 0.5)
if (m * m == n)

题目描述

对于任意大于1的自然数n，若n为奇数，则将n变为3n+1，否则变为n的一半。经过若干次这样的变化，一定可以让n变为1。
输入n，输出变换次数。(n <= 10 ^ 9)。

样例

样例输入：
3
样例输出：
7

#include <iostream>

using namespace std;

int main() {
    long long n, cnt = 0;
    cin >> n;

    while (n > 1) {
        if (n % 2 == 1)
            n = 3 * n + 1;
        else
            n /= 2;
        //cout << n << endl;
        cnt ++ ;
    }

    cout << cnt << endl;
    return 0;
}

计算∏/4 = 1 - 1/3 + 1/5 - 1/7 + …,直到最后一项小于10^-6.

#include <iostream>

using namespace std;

int main() {
    double sum = 0, term;
    int i = 0;
    /*for (int i = 0; ; i ++ ) {

        double term = 1.0 / (i * 2 + 1);

        if (i % 2 == 0)
            sum += term;
        else
            sum -= term;

        if (term < 1e-6)
            break;
    }*/

    do {
        term = 1.0 / (i * 2 + 1);

        if (i % 2 == 0)
            sum += term;
        else
            sum -= term;
        i ++ ;
    } while (term >= 1e-6);

    printf("%.6lf\n", sum);
    return 0;
}

题目描述

输入n，输出S = 1！+ 2！+ 3！+ … + n！的末6位(不含前导零).n<= 10 ^ 6,n!表示前n个正整数之积。

样例

样例输入：
10
样例输出：
37913

做法1

#include <iostream>

using namespace std;

int main() {
    int n, S = 0;
    cin >> n;

    for (int i = 1; i <= n ; i ++ ) {

        int factorial = 1;

        for (int j = 1; j <= i; j ++ )

            factorial *= j;
        S += factorial;
    }

    printf("%d\n", S % 1000000);
    return 0;
}

做法2

#include <iostream>
#include <time.h>

using namespace std;

const int mod = 1e6;

int main() {
    int n, S = 0;
    cin >> n;

    for (int i = 1; i <= n ; i ++ ) {

        int factorial = 1;

        for (int j = 1; j <= i; j ++ )

            factorial = factorial * j % mod;
        S = (S + factorial) % mod;
    }

    printf("%d\n", S);
    printf("Time used = %.2f\n", (double)clock() / CLOCKS_PER_SEC);
    return 0;
}

总结

要计算只包含加法、减法和乘法的整数表达式除以正整数n的余数，可以在每一步计算之后对n取模，结果不变。

水仙花数

题目描述

输出100~999中的所有水仙花数。若3位数ABC满足ABC = A^3 + B^3 + C^3，则称其为水仙花数。例如153 = 1^3 + 5^3 + 3^3，所以153是水仙花数。

#include <iostream>

using namespace std;

int F(int a, int b, int c) {
    return a * a * a + b * b * b + c * c * c;
}

int main() {
    for (int i = 100; i <= 999; i ++ ) {

        int a = i / 100;
        int b = i / 10 % 10;
        int c = i % 10;

        if (F(a, b, c) == i)
            cout << i << endl;
    }

    return 0;
}

韩信点兵

题目描述

相传韩信才智过人，从不直接清点自己军队的人数，只要让士兵先后以三人一排、五人一排、七人一排地变换队形，而他每次只掠一眼队伍的排尾就知道总人数了。输入包含多组数据，每组数据包含3个非负整数a,b,c，表示每种队形排尾的人数(a<3, b<5,c<7)，输出总人数的最小值(或报告无解)。已知总人数不小于10，不超过100。输入到文件结束为止。

样例

样例输入：
2 1 6
2 1 3
样例输出：
Case 1: 41
Case 2: No answer

#include <iostream>

using namespace std;

int main() {
    int a, b, c, casei = 0;

    while (scanf("%d%d%d", &a, &b, &c) != EOF) {
        printf("Case %d: ", ++ casei);
        int flag = 0;

        for (int i = 10; i <= 100; i ++ )

            if (i % 3 == a && i % 5 == b && i % 7 == c) {
                cout << i << endl;
                flag = 1;
                break;
            }

        if (!flag)
            cout << "No answer\n";
    }

    return 0;
}

倒三角形

题目描述

输入正整数n<=20，输出一个n层的倒三角形。例如，n = 5时输出如下：

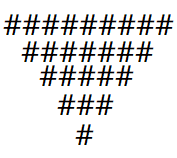
#include <iostream>

using namespace std;

int main() {
    int n;
    cin >> n;

    for (int i = 1; i <= n; i ++ ) {

        for (int j = 1; j < i; j ++ )

            cout << " ";

        for (int k = 1; k <= 2 * (n + 1 - i) - 1; k ++ )

            cout << "#";
        cout << endl;
    }

    return 0;
}

子序列的和

题目描述

输入两个正整数n<m<$10^6$，输出$1/n^2 + 1/(n + 1)^2 + … + 1/m^2$，保留5位小数。输入包含多组数据，结束标记为n=m=0。提示：本题有陷阱。

样例

样例输入：
2 4
65536 655360
0 0
样例输出：
Case 1：0.42361
Case 2：0.00001

#include <iostream>

using namespace std;

int main() {
    int n, m, casei = 0;

    while (cin >> n >> m) {
        double s = 0;

        if (n == 0 && m == 0)
            break;

        if (n == m)
            s = 2 * (1 / (n * n));
        else {
            for (double i = n; i <= m; i ++ )

                s += 1 / (i * i);
        }

        printf("Case %d：", ++ casei);
        printf("%.5lf\n", s);
    }

    return 0;
}

分数化小数

题目描述

输入正整数a,b,c，输出a/b的小数形式，精确到小数点后c位。a,b<=$10^6$,c<=100。
输入包含多组数据，结束标记为a=b=c=0。

样例

样例输入：
1 6 4
0 0 0
样例输出：
Case 1：0.1667

#include <iostream>
#include <iomanip>

using namespace std;

int main() {
    int a, b, c, casei = 0;

    while (cin >> a >> b >> c) {
        if (a == 0 && b == 0 && c == 0)
            break;
        double s = (double)a / b;
        printf("Case %d：", ++ casei);
        cout << fixed << setprecision(c) << s << endl;
    }

    return 0;
}

排列

题目描述

用1,2,3,…,9组成3个三位数abc，def和ghi，每个数字恰好使用一次，要求abc：def：ghi = 1：2：3。按照“abc def ghi”的格式输出所有解，每行一个解。提示：不必太动脑筋。

#include <iostream>

using namespace std;

bool check(int a, int b, int c) {
    if (((a / 100 + a / 10 % 10 + a % 10 + b / 100 + b / 10 % 10 + b % 10 + c / 100 + c / 10 % 10 + c % 10) == 1 + 2 + 3 + 4
            + 5 + 6 + 7 + 8 + 9)
            && (((a / 100) * (a / 10 % 10) * (a % 10) * (b / 100) * (b / 10 % 10) * (b % 10) * (c / 100) * (c / 10 % 10) *
                 (c % 10)) == 1 * 2 * 3 * 4 * 5 * 6 * 7 * 8 * 9))
        return true;
    else
        return false;
}

int main() {
    for (int i = 123; i <= 333; i ++ ) {

        int j = 2 * i;
        int k = 3 * i;

        if (check(i, j, k))
            cout << i << ' ' << j << ' ' << k << endl;
    }

    return 0;
}