https://codeforces.com/contest/1543/problem/A

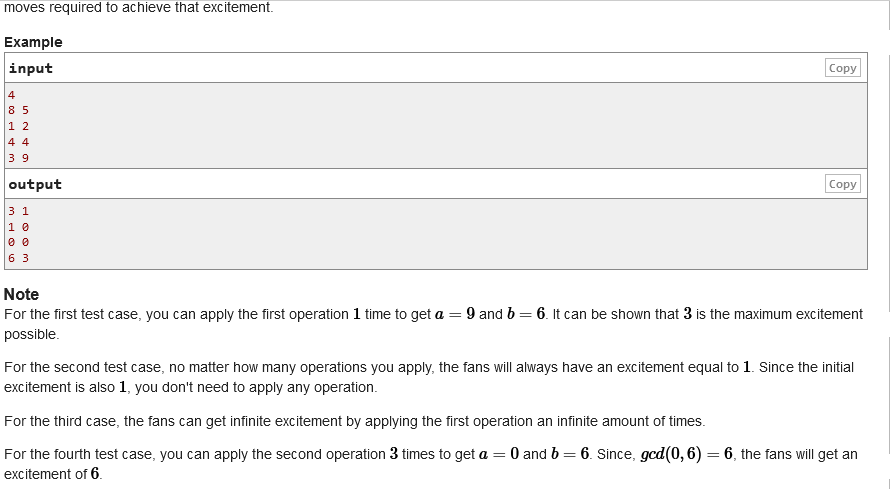
You know, the greatest common divisor of any positive integer and 0 is itself.
First, if two numbers are equal, then their greatest common divisor is themselves. If they are not equal, let’s record ‘U’ as the first output. We first prove that u > = a-b. First of all, let ‘a’ be a larger number. After B subtraction operations, the greatest common factor of the two numbers is A-B, so u > = a-b.
Next, we prove that U < = a-b. Suppose U > A-B, because u is the greatest common divisor after a and B change, which can be considered as the greatest common factor of (a + x) and (B + x), then u * A1 = (a + x), u * B1 = (B + x), then u * a1-u * B1 = u * (a1-b1) = A-B, so A-B can divide U. And because a is not equal to B, U < = a-b.
So the first output is u = a-b.
Now let’s consider the second output. To ensure that the common factor of the two numbers is u, we just need to make a and B become multiples of U. for example, u is 7, a is 100, we know that 100 / 7 = 14. We have two ways to go. One is to make a 7 * 14, the other is to make a 7 * 15, which operation times are less.

Code:

#include<bits/stdc++.h>

using namespace std;

typedef long long ll;

ll t, a, b;

int main()
{
    cin >> t;
    while(t --)
    {
        cin >> a >> b;
        if(a == b) cout << 0 << ' ' << 0 << endl;
        else
        {
            if(a < b) swap(a, b);
            ll u = a - b;
            cout << u << ' ' << min(a - a / u * u, a / u * u + u - a) << endl;
        }
    }
}