https://codeforces.com/contest/1543/problem/B

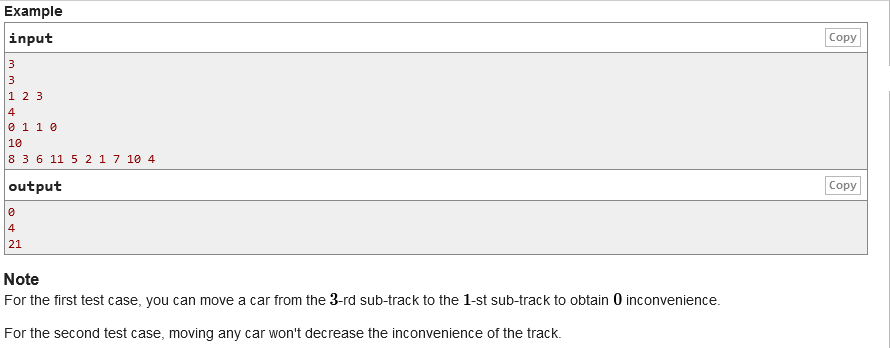
You can distribute all the numbers at any position to minimize the sum of the two differences.
It’s very simple. We just need to make the numbers as evenly distributed as possible.
For example, in the last example, if 57 is distributed in 10 positions, then it is 3 5’s and 7 6’s. If the difference between 5 and 5 is 0, each 5 and each 6 will produce a difference of 1. If there are 3 5’s and 7 6’s, they will produce 3 * 7 = 21 1. The total is 21.
We find that if 17, 27 and 37 are distributed in 10 positions, the same result will be obtained, which is in line with our idea of modular operation.
Under the premise of uniform distribution of each position, the number of large numbers is the sum / number of positions, and the number of small numbers is the number of n-large numbers.

Code:

#include<bits/stdc++.h>

using namespace std;

typedef long long ll;

ll t, n, res, u;

int main()
{
    cin >> t;
    while(t --)
    {
        cin >> n;
        res = 0;
        for(int i = 1; i <= n; i ++) cin >> u, res += u;
        cout << (res % n) * (n - res % n) << endl;
    }
}