https://codeforces.com/contest/1543/problem/D1

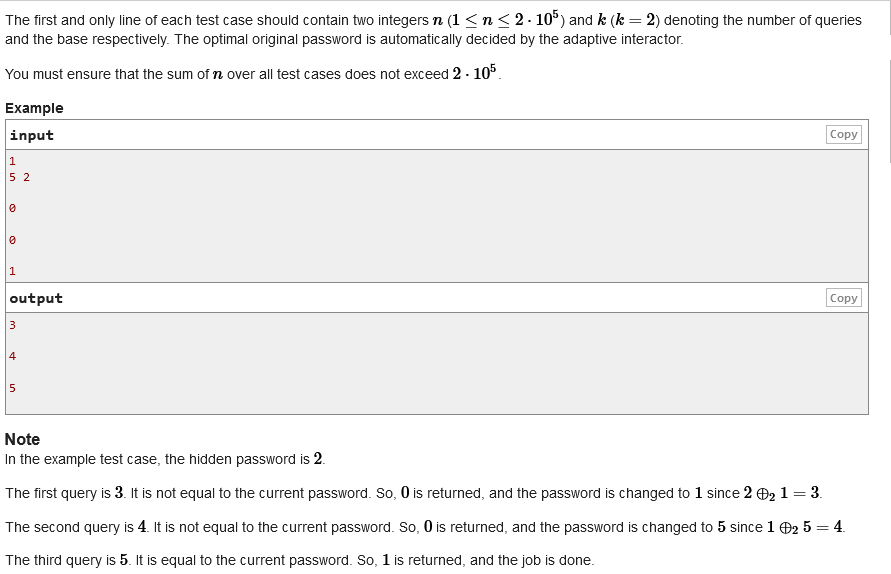
First of all, let’s explain the meaning of the topic
The title gives you n and K values first, and the title secretly generates a password by itself. Your goal is to guess the password.The initial value of this password is not greater than n, that is, 0 to n-1, and you can guess n times, which means you can enumerate each possibility, from 0 to n-1.
The problem, however, is that every time you ask, the password changes dynamically and the rules are as follows:
First, D1 is simpler, you just need to consider the XOR operation in binary. The rule is that when you ask if the password is t, the password changes from X to y, where x XOR y equals t.Here we need to push a formula, if x^y=t, then x^y^x=t^x, and because x^y^x=y, y=t^x=x^y.That is, every time you ask t, the password will be on the original basis ^=t.
Obviously, if you ask u, the password will become K ^ u. if you ask u ^ t at this time, the password will become K ^ u ^ u ^ t = k ^ t, so we can cancel the original number every time we ask. Theoretically, we can use two questions from 0 to n-1.
But if we do this, we need to ask 2 * n-2 times, which is beyond the limit. We need to continue to optimize, such as merging the two queries. In addition to asking 0 for the first time, we can ask I * (I + 1) for each time, so that the previous access can be offset, and the password for each time is k ^ 0, K ^ 1, K ^ 2,…, K ^ (n-1)
Next, we need to prove that in n-1 queries, we must get the correct answer again and exit.
If the initial value of the password is 0, it will be obtained in the first query. End.
If the initial value of the password is not 0, then the password becomes K ^ (I-2) before the i-th query, and the query value is (i-1) ^ (I-2). Obviously, when k = I-1, it ends, and K < n, the value of I is 1 to N, which guarantees that this value will be taken and exit.

Code:

#include<bits/stdc++.h>

using namespace std;

typedef long long ll;

int t, n, k;

int main()
{
    cin >> t;
    while(t --)
    {
        cin >> n >> k;

        ll u = 0;

        cout << 0 << endl;

        while(cin >> k && !k) cout << ((u + 1) ^ (u ++)) << endl;
    }
}