https://codeforces.com/contest/1543/problem/D2

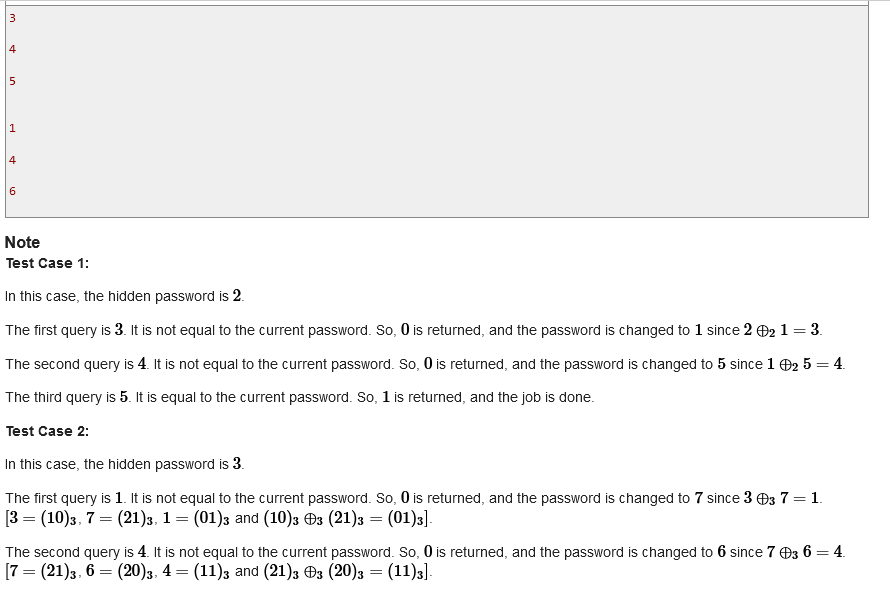
The topic is easy to understand, k-base module, rather than the simple binary
To do this problem, we must first deduce some formulas
If a location is originally a, it becomes C after asking B, satisfying (A + C) mod k = B
So we have, (K + B - A) mod K = C
Next we can find the rule by enumerating the first few cases
Now, let’s record the original answer with X.
If x = 0, then the first time we ask 0 is the answer.
Let (K + a-b) mod K be (a-b)
If x = 1, then after we ask 0, X becomes (0-1), we ask the end of this
If x = 2, then after we ask 0 and (0-1), it becomes ((0-1) - (0-2)) = (2-1), we ask the end
If x = 3, then it becomes ((2-1) - ((0-1) - (0-3))) = (2-1) - (3-1) = (2-3), we ask the end.
So far, we have come to the conclusion that except 0, I can be obtained by I-1 and I by subtraction in the sense of modulo K. And we need to make sure that we subtract the odd from the even.

Code:

#include<bits/stdc++.h>

using namespace std;

typedef long long ll;

int t, n, k;

ll cal(ll u)
{
    ll a = u, b = u;
    if(a & 1) a ++; else b ++;

    ll res = 0, ka = 0, kb = 0, p = 1;

    while(a || b)
    {
        ka = a % k, kb = b % k;
        res += ((k + ka - kb) % k) * p;
        p *= k;
        a /= k, b /= k;
    }

    return res;
}

int main()
{
    cin >> t;
    while(t --)
    {
        cin >> n >> k;

        cout << 0 << endl;

        ll u = 0;

        while(cin >> n && !n) cout << cal(u ++) << endl;
    }
}