二分查找适用于单调函数中逼近求解某点的值。如果遇到凸性或凹形函数时，可以用三分查找求此凸点或凹点。

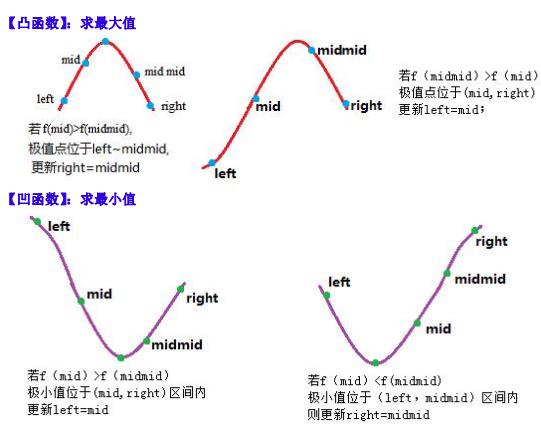
代码：（两种写法，这里均找上凸点）

• 法一：

double f(double a){/*根据题目意思计算*/}
double three(double l,double r) //找凸点
{
    while(l<r-1)
    {
        double mid=(l+r)/2;
        double mmid=(mid+r)/2;
        if(f(mid)>f(mmid)) r=mmid;
        else l=mid;
    }
    if(f(l)>f(r)) return l;
    else return r;
}

• 法二：

double f(double a){/*根据题目意思计算*/}
double three(double l,double r)
{
    while(l+EPS<r)
    {
        double mid=l+(r-l)/3;
        double midmid=r-(r-l)/3;
        if(f(mid)>f(midmid)) r=midmid;
        else l=mid;
    }
    return l;
}