整除分块文献：
https://blog.csdn.net/weixin_45419138/article/details/103446724
题目：https://ac.nowcoder.com/acm/contest/2891/C

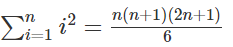
推理1网址：https://www.cnblogs.com/zwfymqz/archive/2019/03/20/10566327.html

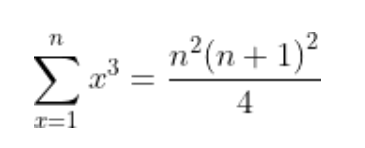
推理2：类似于推理1

#include<iostream>
using namespace std;
const int mod = 1e9+7;
typedef long long ll;
ll n, m;
ll pow(ll a,ll b)
{
    ll res = 1;
    for(;b;b>>=1)
    {
        if(b&1) res = res * a % mod;
        a = a * a % mod;
    }
    return res;
}

ll inv(ll x)
{
    return pow(x,mod-2);
} //上面两个函数是求逆元的 用这个方法来代替除法,避免除法向下取整会对算出的值造成偏差

ll sum_2(ll p) { // i^2 从1加到p的公式
    return p*(p+1)%mod*(2*p+1)%mod*inv(6)%mod;
}

ll sum_3(ll p) { // i^3 从1加到p的公式
    return p*p%mod*(p+1)%mod*(p+1)%mod*inv(4)%mod;
}

int main() 
{
    scanf("%lld %lld", &n, &m);
    ll num1 = n*sum_2(n)%mod; // 求第一个求和公式的值
    for(ll l = 1,r;l <= n; l = r+1) 
    { 
        r = n/(n/l);
        ll t = (sum_3(r)-sum_3(l-1)+mod)%mod;
        t = t * (n/l) %mod;
        num1 = (num1 - t + mod) % mod;
    }

    ll num2 = m*m%mod*(1+m)%mod*inv(2)%mod; // 求第二个求和公式的值
    for(ll l = 1,r;l <= m; l = r+1)
    {
        r = m/(m/l);
        ll t = (sum_2(r)-sum_2(l-1)+mod)%mod;
        t = t *(m/l) %mod;
        num2 = (num2 - t + mod) % mod;
    }
    printf("%lld\n", num1*num2%mod);
    return 0;
}