A.Hdu1165.Eddy’s research II

思路

递推 + 打表 + 找规律

写法1：

#include <iostream>
#include <cmath>

using namespace std;

int n, m;
int Ackermann[4][1000010];

void init()
{
    for(int m = 1; m < 4; m ++ )
        if(m < 3)
            for(int n = 0; n < 1000010; n ++ )
                if(m == 1)
                    Ackermann[m][n] = n + 2;
                else 
                    Ackermann[m][n] = 2 * (n + 1) + 1;
        else
            for(int n = 0; n <= 24; n ++ )
                Ackermann[m][n] = int(pow(double(2), n + 3)) - 3;   //Ackermann[m][n] = Ackermann[m][n-1] * 2 + 3;
}
/*
int Ackermann(int m, int n) 
{
    if(m == 0) return n + 1;
    else
    {
        if(n == 0) 
            return Ackermann(m - 1, 1);
        else 
            return Ackermann(m - 1, Ackermann(m, n - 1));   
    } 
}

void display()
{
    for(int i = 1; i <= 3; i ++ )
    {
        for(int j = 0; j <= 10; j ++ )
            cout << Ackermann(i, j) << "    ";
        cout << endl;
    }

    2       3       4       5       6       7       8       9       10      11      12
    3       5       7       9       11      13      15      17      19      21      23
    5       13      29      61      125     253     509     1021    2045    4093    8189

}
*/
int main()
{
    init();
    while(cin >> m >> n)
    {
        cout << Ackermann[m][n] << endl; 
    }
    return 0;
} 

B.Hdu1286.找新朋友

思路

Euler函数

1. Euler(n) = n * Σ(1 - 1 / p), p | n (p为质因子)

写法1：

#include <iostream>
#include <cmath>

using namespace std;

int t;
int n;

int Euler()
{
    int ans = n;
    for(int i = 2; i <= sqrt(n); i ++ )
        if(n % i == 0)
        {
            ans = ans / i * (i - 1);
            while(n % i == 0)
                n /= i;
        }
    if(n > 1)
        ans = ans / n * (n - 1);
    return ans;
}

int main()
{
    cin >> t;
    while(t -- )
    {
        cin >> n;
        cout << Euler() << endl;
    }
    return 0;
}

C.Hdu1164.Eddy’s research I

思路

质因子(Euler’s p)

写法1：

#include <iostream>
#include <cmath>

using namespace std;

int n;
int Euler_p[65535], len;

void init()
{
    len = 0;
    for(int i = 2; i <= sqrt(n); i ++ )
        while(n % i == 0)
        {
            Euler_p[len ++ ] = i;
            n /= i;
        }
    if(n > 1)
        Euler_p[len ++ ] = n;       
}

int main()
{
    while(cin >> n)
    {
        init();
        for(int i = 0; i < len; i ++ )
            if(i == 0)
                cout << Euler_p[i];
            else
                cout << "*" << Euler_p[i];
        cout << endl;
    }
    return 0;
} 

D.Hdu1215.七夕节

思路

因子(o(√n))

写法1：

#include <iostream>

using namespace std;

int t;
int n;

int main()
{
    cin >> t;
    while(t -- )
    {
        int ans = 0;
        cin >> n;
        for(int i = 1; i * i <= n; i ++ )
            if(n % i == 0)
            {
                ans += i;
                if(n / i != i && i != 1)
                    ans += n / i;
            }
        cout << ans << endl; 
    } 
    return 0;
}

E.Codeforces858A.k-rounding

思路

lcm or 枚举(o(n))

1. lcm(x, y) = x * y / gcd(x, y)

写法1：lcm time1 = 31ms

#include <iostream>
#include <cmath>

using namespace std;

typedef long long ll;

ll n, k;

int gcd(int x, int y)
{
    while(y ^= x ^= y ^= x %= y);
    return x;
}

int main()
{
    cin >> n >> k;
    k = ll(pow(double(10), k));
    cout << n * k / gcd(n, k) << endl;
    return 0;
}

写法2：枚举 time2 = 810ms

ans：[n, n * 10^k]
从小到大枚举，记得break

#include <iostream>
#include <cmath> 

using namespace std;

typedef long long ll;

ll n, k;

int main()
{
    cin >> n >> k;
    k = ll(pow(double(10), k));
    for(int i = k; i <= k; i ++ )
        if(n * i % k == 0) 
        {
            cout << n * i << endl;
            break;  
        } 
    return 0;
}

写法3：dfs time3 = time1 = 31ms

模拟人脑计算

#include <iostream>
#include <cmath>

using namespace std;

typedef long long ll;

ll n, k;

void dfs(ll x)
{
    if(x % k == 0)
    {
        cout << x << endl;
        return ;
    }
    ll xx = x;
    while(xx % 10 == 0) xx /= 10; 
    if((xx % 10 & 1) != 1) dfs(x * 5);
    else
        if(xx % 10 == 5) dfs(x * 2);
        else dfs(x * 10);
}

int main()
{
    cin >> n >> k;
    k = ll(pow(double(10), k));
    dfs(n);
    return 0;
}

F.Hdu4548.美素数

思路

素数 + 打表

写法1：

#include <iostream>

using namespace std;

const int N = 1000010;

int t;
int l, r;
int prime[N];

bool isprime(int x)
{
    if(x == 1) return false;
    for(int i = 2; i * i <= x; i ++ )
        if(x % i == 0)
            return false;
    return true;
}

bool _isprime(int x)
{
    int sum = 0;
    for(; x; x /= 10) sum += x % 10;
    return isprime(sum);
}

void init()
{
    for(int i = 1; i < N; i ++ )
        if(isprime(i) && _isprime(i))
            prime[i] = prime[i - 1] + 1;
        else
            prime[i] = prime[i - 1];
}

int main()
{
    init();
    cin >> t;
    for(int i = 1; i <= t; i ++ )
    {
        cin >> l >> r; 
        printf("Case #%d: %d\n", i, prime[r] - prime[l - 1]);   
    }   
    return 0;
}

G.Poj1061.青蛙的约会

思路

拓展欧几里得算法(exgcd)

1. exgcd：求ax + by = gcd(a, b) 的一组解

x + mt - (y + nt) = kl <=> (n - m)t + lk = x - y
令a = n - m, b = l, c = x - y => ax + by = c
exgcd => ax + by = gcd(a, b) 解 x = _x, y = _y
(x - y) % gcd(a, b) != 0 <=> 题目无解
反之，_x 可能为题目的解（可能 < 0）

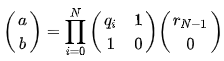
写法1：

#include <iostream>

using namespace std;

typedef long long ll;

ll x, y, m, n, l;

ll exgcd(ll a, ll b, ll &x, ll &y)
{
    if(b == 0) {x = 1, y = 0; return a;}
    ll d = exgcd(b, a % b, x, y), t = x - a / b * y;
    x = y, y = t;
    return d;
}

int main()
{
    cin >> x >> y >> m >> n >> l;
    ll _x, _y, d, r;
    d = exgcd(n - m, l, _x, _y), r = l / d;
    if((x - y) % d)
        cout << "Impossible" << endl;
    else 
        cout << ((x - y) / d * _x % r + r) % r << endl;
    return 0;
}

H.Hdu4704.Sum

思路

欧拉定理 + 费马小定理 + 快速幂

1. 欧拉定理：a^φ(n) ≡ 1 (mod n) (φ(n) Euler’s 函数的值)
2. 费马小定理：a^(p - 1) ≡ 1 (mod p), p为质数
3. 快速幂：位运算求a^n

写法1：

#include <iostream>
#include <string>

using namespace std;

typedef long long ll;

const ll MOD = 1e9 + 7;

string s;

ll pow_mod(ll a, ll n, ll mod)
{
    ll tmp = 1;
    while(n)
    {
        if(n & 1) tmp = tmp * a % mod;
        a = a * a % mod;
        n >>= 1; 
    }
    return tmp;
}

int main()
{
    while(cin >> s)
    {
        ll n = 0;
        for(int i = 0; i < s.size(); i ++ )
            n = (n * 10 + s[i] - '0') % (MOD - 1);
        cout << pow_mod(2, n - 1, MOD) << endl; 
    }
    return 0;
} 

I.Poj2689.Prime Distance

思路

欧拉筛法 + 区间素数筛

用欧拉筛法先筛出一部分（大约前50000，筛到2^16），将区间[l, r] -> [0, <=1e6]，再用欧拉筛法晒出该区间内的质数
倍数区间[(l - 1) / prime[i] + 1, r / prime[i]]（only）

写法1：

#include <iostream>
#include <vector>

using namespace std;

const int N = (1 << 16) + 10;

int l, r; 
int prime[N], tot;
bool vis[N];
bool _vis[N << 4];

void init()
{
    for(int i = 2; i < N; i ++ )
    {
        if(!vis[i]) prime[tot ++ ] = i;
        for(int j = 0; j < tot && i * prime[j] < N; j ++ )
        {
            vis[i * prime[j]] = 1;
            if(i % prime[j] == 0) break;
        }
    }
}

int main()
{
    init(); 
    while(cin >> l >> r)
    {
        for(int i = 0; i < r - l + 1; i ++ ) _vis[i] = 0;
        if(l == 1) _vis[0] = 1;
        for(int i = 0; i < tot; i ++ )
            for(int j = max((l - 1) / prime[i] + 1, prime[i]); j <= r / prime[i]; j ++ )
                 _vis[prime[i] * j - l] = 1;

        int cnt = 0;
        for(int i = 0; i < r - l + 1; i ++ )
            if(!_vis[i]) cnt ++ ;
        if(cnt > 1)
        {
            vector <int> _prime;
            for(int i = 0; i < r - l + 1; i ++ )
                if(!_vis[i]) _prime.push_back(i + l);
            int ans1 = 1, ans2 = 1, maximum = _prime[1] - _prime[0], minimum = _prime[1] - _prime[0];
            for(int i = 2; i < _prime.size(); i ++ )
            {
                if(_prime[i] - _prime[i - 1] > maximum) ans1 = i, maximum = _prime[i] - _prime[i - 1];
                if(_prime[i] - _prime[i - 1] < minimum) ans2 = i, minimum = _prime[i] - _prime[i - 1];
            }
            printf("%d,%d are closest, %d,%d are most distant.\n", _prime[ans2 - 1], _prime[ans2], _prime[ans1 - 1], _prime[ans1]);
        }
        else
            cout << "There are no adjacent primes." << endl;
    }
    return 0;
}

J.Hdu5019.Revenge of GCD

思路

gcd + 因子(o(sqrt(n)))

1 <= t * o(因子) <= 1e8 ==> o(因子) <= o(sqrt(n))

写法1：

#include <iostream>
#include <algorithm>
#include <cmath>
#include <vector>

using namespace std;

typedef long long ll;

int t;
ll x, y, k;

vector <ll> factor;

void init()
{
    factor.clear();
}

ll gcd(ll x, ll y)
{
    while(y ^= x ^= y ^= x %= y);
    return x;
}

int main()
{
    cin >> t;
    while(t -- )
    {
        init();
        cin >> x >> y >> k;
        ll GCD = gcd(x, y);
        for(ll i = ll(sqrt(GCD)); i; i -- )
            if(GCD % i == 0)
            {
                factor.push_back(i);
                if(i * i != GCD)
                    factor.push_back(GCD / i);
            }
        sort(factor.begin(), factor.end());
        ll cnt = factor.size();
        if(cnt < k)
            cout << -1 << endl;
        else
            cout << factor[cnt - k] << endl;
    }
    return 0;
}