详解 膜拜大佬 请点击 Manacher 算法详解

板子题 回文子串的最大长度

切记 以后 凡是涉及 计算字符串长度 一定要先用变量存起来 再跑for循环！！！！

    int len = strlen(s);

manacher算法主要先对原字符串进行处理成奇数串

例如 abcd –> !# a#b#c#d# @

rt 为 最大回文右边界的下一个位置 mid 为回文中心 p[]为最大回文半径

处理后字符串有效位置为 [1, len * 2 + 1]

每次进行计算p[i] 当i < rt 时 有两种情况

1.以mid为中心的最大回文半径 包含 以j为中心的最大回文半径

p[i] = p[mid * 2 - i]

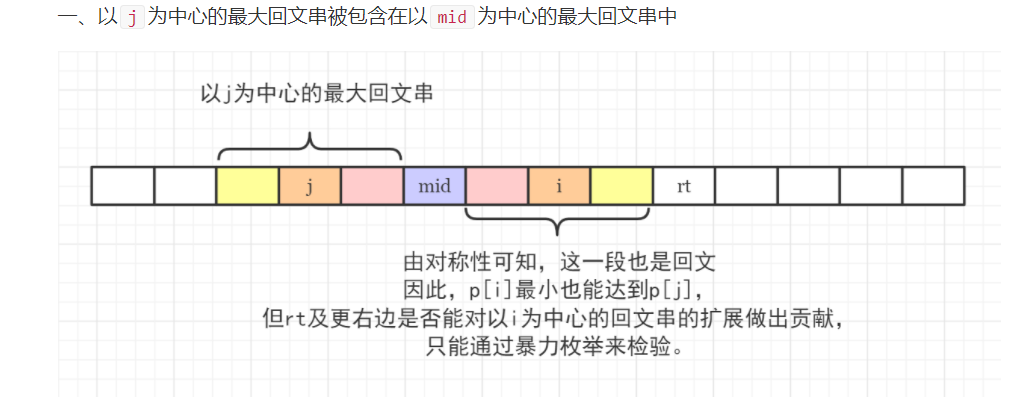
2.以mid为中心的最大回文半径 相交于 以j为中心的最大回文半径

p[i] = rt - i;

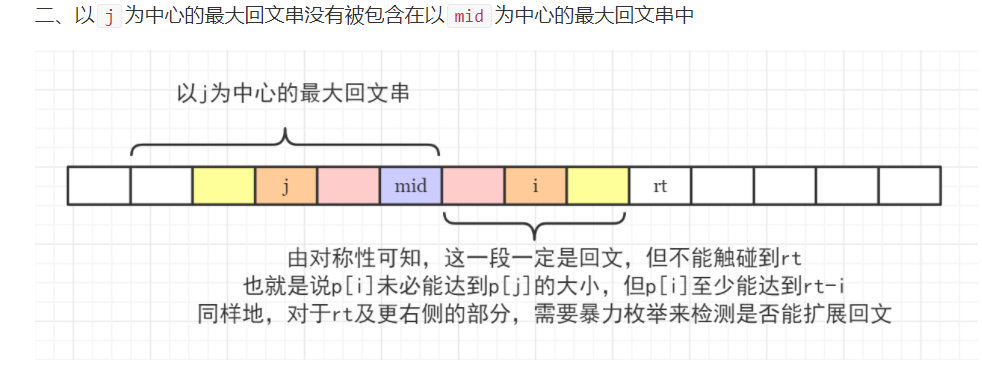
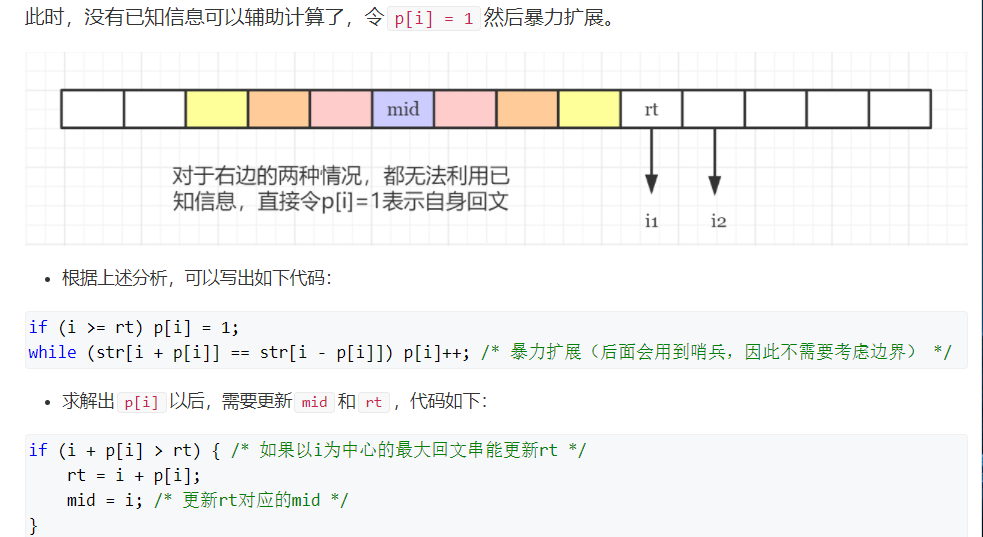
当 i >= rt

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <vector>
#include <map>
#include <set>
#include <queue>
#include <stack>
#include <unordered_map>

using namespace std;
typedef long long ll;
const int INF = 0x3f3f3f3f;
const int maxn = 2e6 + 10;
typedef pair <int, int> PII;
char s[maxn], str[maxn];
int m, p[maxn], cnt;
void manacher(char c[])
{
    int rt = 0, mid = 0;
    int ans = 0;
    for(int i = 1 ; i <= m ; i ++)
    {
        p[i] = (i < rt) ? min(p[mid * 2 - i], rt - i) : 1;
        while(c[i + p[i]] == c[i - p[i]]) //              能够保证始终没有出界
        p[i] ++;
        if(i + p[i] > rt)
        {
            rt = i + p[i];
            mid = i;
        }
        ans = max(ans, p[i] - 1);
    }
    printf("Case %d: %d\n",cnt ++, ans);
}
int main()
{
    cnt = 1;
    while(scanf("%s", s))
    {
        if(s[0] == 'E')
        break;
        str[0] = '!';
        str[1] = '#';
        int len = strlen(s);
        for(int i = 0 ; i < len ; i ++)
        {
            str[i * 2 + 2] = s[i];
            str[i * 2 + 3] = '#';
        }
        m = len * 2 + 1;
        str[m + 1] = '@';
        manacher(str);
//      cout << str << "\n";
    }
    return 0;
}