一、单调队列优化

多重背包

$N$ 个物品，每个物品重量是 $w[i]$，价值是 $v[i]$，个数有 $m[i]$ 个，你现在有一个容量为 $C$ 的背包，问重量不超过背包容量的情况下，能拿到的最大价值

分析：

设 f[i][j] 表示考虑前 $i$ 个物品，背包容量为 $j$ 的时候，能取到的最大价值

$$ f[i][j] = \Big\{f[i-1][j-k\*w[i]] + k\*v[i]\Big\}, \ k \in [0, \min(m[i], \lfloor\frac{j}{w[i]}\rfloor)] $$

需要用三层循环，时间复杂度 $O(n^3)$，能否优化？

优化思路：单调队列

• 先观察，对于每一个状态，它只能由 $j-k\* w[i]$ 转移而来，也就是说，能影响它的点，是模 $w[i]$ 同余的点，其他点不需要考虑
• 那么我们可以把每一行的状态，按照模 $w[i]$ 的余数分组，单独计算。每一组之间互相不影响。
• 那么每一组内如何优化呢？

先看一个例子：取 $m[i] = 2$，$v[i] = v$，$w[i] = w$，$C > 9 \* w$

并假设 $f(j) = F[i-1][j]$，观察公式右边要求最大值的几项：

$j = 6\*w$：$f(6\*w)$、$f(5\*w)+v$、$f(4\*w)+2\*v$ 这三个中的最大值
$j = 5\*w$：$f(5\*w)$、$f(4\*w)+v$、$f(3\*w)+2\*v$ 这三个中的最大值
$j = 4\*w$：$f(4\*w)$、$f(3\*w)+v$、$f(2\*w)+2\*v$ 这三个中的最大值

显然，右边求最大值的几项随 $j$ 值改变而改变，但如果将 $j=6\*w$ 时，每项减去 $6\* v$，$j=5\* w$ 时，每项减去 $5\* v$，$j = 4\* w$ 时，每项减去 $4\* v$，就得到：

$j = 6\*w$：$f(6\*w) - 6\* v$、$f(5\*w)-5\* v$、$f(4\*w)-4\*v$ 这三个中的最大值
$j = 5\*w$：$f(5\*w) - 5\* v$、$f(4\*w)-4\* v$、$f(3\*w)-3\*v$ 这三个中的最大值
$j = 4\*w$：$f(4\*w) - 4\* v$、$f(3\*w)-3\* v$、$f(2\*w)-2\*v$ 这三个中的最大值

这里就有重复项了，相当于一个长度为 $3$ 的滑窗最大值，可以直接用单调队列 $O(1)$ 求出

例题：P1776 宝物筛选

小 FF 对洞穴里的宝物进行了整理，他发现每样宝物都有一件或者多件。他粗略估算了下每样宝物的价值，之后开始了宝物筛选工作：小 FF 有一个最大载重为 $W$ 的采集车，洞穴里总共有 $n$ 种宝物，每种宝物的价值为 $v_i$，重量为 $w_i$，每种宝物有 $m_i$ 件。小 FF 希望在采集车不超载的前提下，选择一些宝物装进采集车，使得它们的价值和最大。

C++ 代码

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using std::cin;
using std::cout;
using std::min;

const int MX = 40005;

struct Node {
    int val, pos;
} q[MX];

int dp[MX];

int main() {
    int n, c;
    cin >> n >> c;

    rep(i, n) {
        int v, w, m;
        cin >> v >> w >> m;
        m = min(m, c/w);

        rep(r, w) { // 枚举模 w 的每个余数
            int head = 0, tail = 0;
            for (int k = 0; k*w+r <= c; ++k) {
                int j = k*w+r;
                while (head < tail and q[head].pos < k-m) head++;
                while (head < tail and q[tail-1].val < dp[j]-k*v) tail--;
                q[tail].val = dp[j]-k*v;
                q[tail++].pos = k;
                dp[j] = q[head].val+k*v;
            }
        }
    }

    cout << dp[c] << '\n';

    return 0;
}

二、斜率优化

根据函数凸性进行优化

分组 DP

将 $n$ 个物品分为连续的若干份（不限制份数），每份一次会产生一个代价（告诉那代价的计算方式），问代价最大/最小是多少。

用线性 $\rm{DP}$ 来解决该问题。设 f[i] 表示选择前 $i$ 个物品的最小（最大）代价，则

$$ f[i] = \min\{f[j] + w(j, i)\} $$

其中 w(j, i) 表示从 $j$ 到 $i$ 的转移代价，$1 \leqslant j \leqslant i$
朴素做法一次转移的复杂度是 $O(n)$

转移代价为每组物品中每个物品代价之和

设每个物品代价为 $a[i]$，如果 $w(j, i) = \sum\limits_{k=j+1}^i a[k]$

我们设 $a[i]$ 数组的前缀和为 sum[i]，则

$$ f[i] = \min\{f[j] + sum[i] - sum[j]\} = sum[i] + \min\{f[j] - sum[j]\} $$

只需要用一个变量维护前面见过的所有 f[j] - sum[j] 的最小值即可。如果要求每组不能超过 $k$ 个元素，可以用单调队列维护滑窗最小值。

不过如果代价中包含既含有 $i$，又含有 $j$ 的项，单调队列就不行了

例题1：P2365 任务安排

$n$ 个任务排成一个序列在一台机器上等待完成（顺序不得改变），这 $n$ 个任务被分成若干批，每批包含相邻的若干任务。

从零时刻开始，这些任务被分批加工，第 $i$ 个任务单独完成所需的时间为 $t_i$。在每批任务开始前，机器需要启动时间 $s$，而完成这批任务所需的时间是各个任务需要时间的总和（同一批任务将在同一时刻完成）。

每个任务的费用是它的完成时刻乘以一个费用系数 $f_i$。请确定一个分组方案，使得总费用最小。

分析：

设 t[i] 表示每个任务需要的时间的数组的前缀和，c[i] 表示每个任务的费用系数的前缀和
f[i] 为前 $i$ 个任务分成若干批的最小费用，用前面的思想，从 $j$ 状态转移到 $i$ 状态

但是比较麻烦的是，我们并不知道 $j$ 状态的时候，分了多少批，而后面的代价计算又跟前面分了几批有关，因为分批数目决定了后续任务的结束时间

我们换一个思路，把费用计算提前，当目前决定从 $j+1$ 位置开始分组，则 $j+1$ 位置及以后所有元素都要多 $S$ 秒的启动时间带来的费用

$$ f[i] = \min_{j=0}^{i-1} \{f[j] + (c[i] - c[j]) \times t[i] + S \times (c[n] - c[j])\} $$

这样时间复杂度是 $O(n^2)$ 足够通过本题。

抛开这道题不谈，能否进一步优化？

把柿子里的 $\min$ 去掉，整理一下

$$ f[j] = (t[i]+S) \times c[j] + f[i] - c[i] \times t[i] - S \times c[n] $$

我们把 c[j] 当做横轴 $x$，把 f[j] 当做纵轴 $y$，则上述柿子可以看做一次函数，图像是一条直线
直线的斜率是 t[i]+S，截距是 f[i]-c[i]*t[i]-S*c[n]
随着 $j$ 的增加，c[j] 和 f[j] 都是增加的
我们求 f[i] 的最小值，其实是找一条斜率是 t[i]+S 的红色直线，经过某个点，且截距最小
图中 1-4 号点在 “下凸壳”上，此时 $2$ 号点会被经过的条件是 $k_1 < k < k_2$

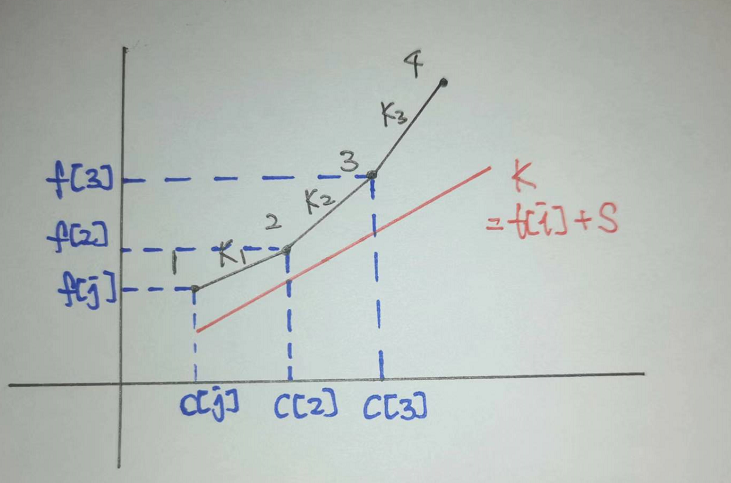
凸壳

• 如左图，$2$ 号点没有机会被选中，但是右图中每个点都是有机会的
• 我们可以用单调队列维护下凸壳点集，把队尾没有机会被选中的点，直接丢弃掉
• 本题中，线段的斜率是递增的，所以开头两点的斜率如果小于 $k$，也可以直接丢弃队头

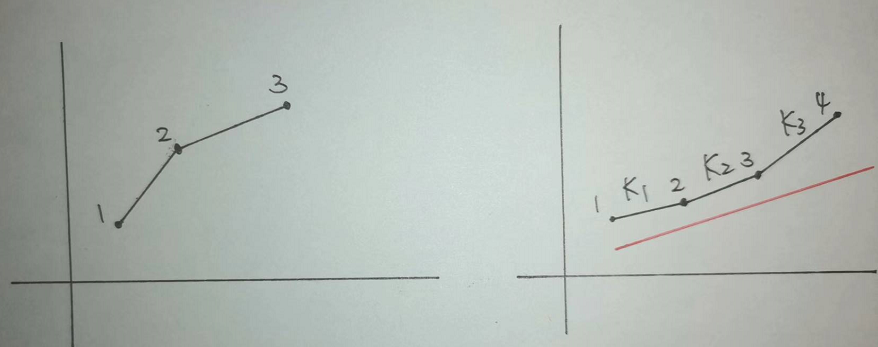
C++ 代码

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 1; i <= (n); ++i)

using std::cin;
using std::cout;
using ll = long long;

const int MX = 5005;

ll t[MX], c[MX], q[MX], f[MX];

int main() {
    int n, s;
    cin >> n >> s;

    rep(i, n) {
        cin >> t[i] >> c[i];
        t[i] += t[i-1];
        c[i] += c[i-1];
    }

    int head = 0, tail = 0;
    rep(i, n) {
        while (tail-head >= 2) {
            int x = q[tail-2], y = q[tail-1], z = i-1;
            if ((f[y]-f[x])*(c[z]-c[y]) < (c[y]-c[x])*(f[z]-f[y])) {
                break;
            }
            tail--;
        }
        q[tail++] = i-1;

        while (tail-head >= 2) {
            int x = q[head], y = q[head+1];
            if ((c[y]-c[x])*(t[i]+s) < (f[y]-f[x])) {
                break;
            }
            head++;
        }
        // 现在队头是我们要的点
        int j = q[head];
        f[i] = f[j] - (t[i]+s)*c[j] + c[i]*t[i] + s*c[n];
    }

    cout << f[n] << '\n';

    return 0;
}

例题2：玩具装箱

记 f[i] 表示前 $i$ 个数压缩的最小费用，sum[i] 表示前 $i$ 个玩具压缩完的长度之和

转移方程：

设前 $j$ 个玩具各自压缩， $j + 1 \sim i$ 分为一组，可得

$ \begin{aligned} f[i] &= \min\Big\{f[j] + \big[i - (j+1) + \sum\limits_{k=j+1}^i c_k - L\big]^2\Big\}\\\ &= \min\Big\{f[j] + (i-j-1 + sum[i]-sum[j] - L)^2\Big\} \end{aligned} $

为了简化计算，令 $g[i] = i +sum[i]$，$h[i] = i+sum[i]+1+L$
去掉 $\min$ 符号可得

$$ f[i] = f[j] + (g[i] - h[j])^2 $$

打开括号，整理一下，只有 $j$ 的项放在等号左边，交叉项放右边，只有 $i$ 的当常数，得

$$ f[j] + h[j]^2 = 2g[i]h[j] + f[i] - g[i]^2 $$

可以把 $f[j] + h[j]^2$ 当纵坐标，$h[j]$ 当横坐标，直线的斜率是 $2g[i]$

当 $i$ 固定的时候，斜率是固定的，截距里面 $g[i]$ 是固定的，所以截距最小的时候，f[i] 取到最小值

然后我们只需用单调队列维护一个下凸壳即可

C++ 代码

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 1; i <= (n); ++i)

using ll = long long;

const int MX = 50005;

int n, L;
ll c[MX], f[MX], sum[MX], g[MX], h[MX];
ll q[MX], head, tail; //维护一个单调队列

//f[j]+h[j]^2 = 2g[i]h[j] + f[i]-g[i]^2
int main() {
    scanf("%d%d", &n, &L);
    h[0] = 1 + L;
    rep(i, n) {
        scanf("%lld", &c[i]);
        sum[i] = sum[i - 1] + c[i];
        g[i] = i + sum[i];
        h[i] = g[i] + 1 + L;
    }

    rep(i, n) {
        //先把上次的i-1放进队尾
        //如果单调队列里面元素超过2个，检查队尾是否要弹出
        while (tail - head >= 2) {
            //x是倒数第二个，y是队尾，z是新来的
            int x = q[tail-2], y = q[tail-1], z = i-1;
            if (((f[y] + h[y] * h[y]) - (f[x] + h[x] * h[x])) * (h[z] - h[y]) <
                ((f[z] + h[z] * h[z]) - (f[y] + h[y] * h[y])) * (h[y] - h[x])) {
                break;
            }
            tail--;
        }
        q[tail++] = i-1;
        //如果队头两个点斜率小于当前要的直线的斜率，弹出队头
        while (tail - head >= 2) {
            int x = q[head], y = q[head+1];
            if ((f[y] + h[y] * h[y]) - (f[x] + h[x] * h[x]) > 2 * g[i] * (h[y] - h[x])) {
                break;
            }
            head++;
        }
        //现在可以从队头转移了
        int j = q[head];
        f[i] = f[j] + h[j] * h[j] + g[i] * g[i] - 2 * g[i] * h[j];
    }

    printf("%lld\n", f[n]);

    return 0;
}

三、数据结构优化

四、决策单调性优化

五、概率与期望

一些前置技能

设某单一随机事件 $A$ 发生的概率为 $P(A)$，那么 $A$ 的互斥事件为 $A^c$，$P(A \cup A^c) = 1$

在事件 $A$ 的前提下发生事件 $B$ 的概率为 $P(B \mid A)$，显然有

$$ P(B \mid A) = \frac{P(AB)}{P(A)} $$

对于无交集的事件 $A, B$，有 $P(A \cup B) = P(A) + P(B)$

对于有交集的事件 $A, B$，$P(A \cup B) = P(A) + P(B) - P(A) * P(B)$

$A$ 事件发生的期望 $E(A)$ 被定义为 $E(A) = P(A) * val(A)$ 即概率乘以取值，期望能够很好的衡量事件的平均程度。

期望具有线性，简单的说即对于两个变量 $A, B$，

$$ E(A + B) = E(A) + E(B) \tag{1} $$

例1：Favorite Dice link

一个 $n$ 面的骰子，求期望掷几次能使得每一面都被掷到。

分析：

• 记 $f[i]$ 表示 $n$ 面骰子掷到 $i$ 个不同面，期望多少次停下
• $f[i] = \frac{i}{n} * f[i] + \frac{n - i}{n} * f[i + 1] + 1, \ 0 \leqslant i \leqslant n$
• 移项可得，$f[i] = f[i + 1] + \frac{n}{n - i}$
• 答案就是 $f[0]$
• 其实手算一下答案就是 $n(1 + \frac{1}{2} + \cdots + \frac{1}{n})$

Code:

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 1; i <= (n); ++i)

using std::cin;
using std::cout;

int main() {
    int t;
    cin >> t;

    while (t--) {
        int n;
        cin >> n;
        double sum = 0;
        rep(i, n) sum += 1.0 / i;
        double ans = n * sum;
        printf("%.2f\n", ans);
    }

    return 0;
}

例2：Red is good link

桌面上有 $A$ 张红牌与 $B$ 张黑牌，随机打乱放置。现在开始一张一张的翻开，翻到红牌加一分，黑牌减一分，求在最优策略的情况下的期望得分。
$A, B \leqslant 5000$

分析：

描述手里的牌可以做但是比较麻烦，不妨描述桌子上剩下的牌
考虑用 $f(i, j)$ 表示桌子上还剩下 $i$ 张红牌与 $j$ 张黑牌时期望的最佳利益，分类讨论一下
当 $i = 0$ 时 $f(i, j) = 0$
当 $j = 0$ 时 $f(i, j) = i$
否则的话，$f_{i,j} = \max(0, \frac{i}{i + j}(1 + f_{i - 1,j}) + \frac{j}{i + j}(-1 + f_{i, j - 1}))$
这样的话答案其实就是 $f(n, m)$，注意到 $5000^2$ 会 MLE，需要滚动一下。

Code

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using std::cin;
using std::cout;
using std::max;

const int MX = 5005;
double f[2][MX];

int main() {
    int n, m;
    cin >> n >> m;

    rep(i, n + 1) {
        rep(j, m + 1) {
            if (i == 0) f[i & 1][j] = 0;
            if (j == 0) f[i & 1][j] = i;
            f[i & 1][j] = max(0.0, (f[i - 1 & 1][j] + 1) * i / (i + j) + (f[i & 1][j - 1] - 1) * j / (i + j));
        }
    }

    printf("%.6lf\n", f[n & 1][m] - 0.0000005);

    return 0;
}

例3： OSU! link

一共有 $n$ 次操作，第 $i$ 次操作有 $a_i$ 的概率为 $1$，$n$ 次操作对应为 $1$ 个长度为 $n$ 的 $01$ 串。定义这个 $01$ 串的权值为所有极长的 $1$ 的长度的立方和。求最后得分的期望。
如：$010001$ 权值是 $1^3 + 1^3$，$101110$ 权值是 $1^3 + 3^3$。

分析：

首先需要注意，平方的期望不等于期望的平方，因为概率不会随权值平方。

$$ (x + 1)^3 - x^3 = 3x^2 + 3x +1 $$

分别求长度的期望，长度平方的期望以及在 $i$ 位置时的期望得分即可。

Code

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 1; i <= (n); ++i)

using std::cin;
using std::cout;

const int MX = 100005;
double p[MX], f[MX], g[MX], h[MX];

int main() {
    int n;
    cin >> n;

    rep(i, n) cin >> p[i];

    rep(i, n) {
        g[i] = p[i] * (g[i - 1] + 1); // 在 i 位置时，后缀 1 的期望长度
        h[i] = p[i] * (h[i - 1] + 2 * g[i - 1] + 1); // 在 i 位置时，后缀 1 的期望长度的平方
        f[i] = p[i] * (f[i - 1] + 3 * h[i - 1] + 3 * g[i - 1] + 1) + (1 - p[i]) * f[i - 1]; 
    }

    printf("%.1f\n", f[n]);

    return 0;
}

例4：Check the difficulty of problems link

现在有 $t$ 支队伍在做题，一共有 $m$ 道题，第 $i$ 个队伍做出第 $j$ 道题的概率为 $p(i, j)$。
现在比赛主办方希望每个队伍都至少做对一道题，且至少有一个队伍做对 $n$ 道及以上的题，问多大概率发生这种情况。
$0 < m \leqslant 30, \ 1 < t \leqslant 1000, 0 < n \leqslant m$

分析：

对于每个队伍，$1 - P$(爆零) 就是不爆零的概率。
对于一个队伍，通过简易的 $DP$ 可以得出其 $A$ 掉 $x$ 道题的概率，那么对于 $x \geqslant k$ 的概率求个和就是超过 $k$ 部分的概率。
直接乘在一起。
然后你就 GG 了，由于这两件事件之间有交集，所以不能直接用概率相乘。

换一个想法考虑，我们设事件 $A$ 为所有队伍都过了至少一道题目，设事件 $B$ 为存在队伍过了 $k$ 道题目。
由

$$P(AB) + P(AB^c) = P(A)$$

移项就能得到

$$P(AB) = P(A) - P(AB^c)$$

等号左边是所求，右边的部分能通过刚才的 $DP$ 解决。

Code

#include <iostream>
#include <cstdio>
#define rep(i, n) for (int i = 1; i <= (n); ++i)

using std::cin;
using std::cout;

double p[1005][35];
double dp[35][35]; // 前 i 道题里做出了 j 个 

int main() {
    int m, t, n;
    double p1, pn, pi;

    while (cin >> m >> t >> n and (m + t + n)) {
        memset(p, 0, sizeof p);
        memset(dp, 0, sizeof dp);

        rep(i, t)rep(j, m) cin >> p[i][j]; // 第 i 个队 ac 第 j 题的概率 

        // 计算 p1 >= 1
        p1 = 1;
        rep(i, t) {
            pi = 1;
            rep(j, m) pi *= (1 - p[i][j]);
            p1 *= (1 - pi);
        } 

        // 计算 pn
        pn = 1;
        rep(i, t) {
            dp[0][0] = 1;
            rep(j, m) {
                dp[j][0] = dp[j - 1][0] * (1 - p[i][j]);
                for (int k = 1; k < j; ++k) {
                    dp[j][k] = dp[j - 1][k] * (1 - p[i][j]) + dp[j - 1][k - 1] * p[i][j];
                }
                dp[j][j] = dp[j - 1][j - 1] * p[i][j];
            }
            pi = 0;
            for (int j = 1; j < n; ++j) {
                pi += dp[m][j];
            }
            pn *= pi;
        }
        printf("%.3f\n", p1 - pn); 
    }

    return 0;
}

六、矩阵快速幂优化

矩阵乘法

矩阵

一个 $n \times m$ 的矩阵可以看做一个 $n$ 行 $m$ 列的二维数组。

$$ \begin{pmatrix} a[1][1] & \cdots & a[1][m]\\\ \vdots & \ddots & \vdots\\\ a[n][1] & \cdots & a[n][m] \end{pmatrix} $$

矩阵加法

两个大小相同的矩阵可以相加/减。
只要把同一个位置的两个数相加/减即可。

${\color{Blue} {A+B = [a_{ij} + b_{ij}]}}$
${\color{Blue} {A-B = [a_{ij} - b_{ij}]}}$

矩阵乘以数字

矩阵可以乘上一个数字。
只要把矩阵中的每个数都乘上那个数字即可。

${\color{Blue} k}{\color{Red} A} {\color{Blue} {= [ka_{ij}]}}$

矩阵乘法

一个大小为 $n \times {\color{Red} m}$ 和一个大小为 ${\color{Red} m} \times r$ 的矩阵可以相乘。
得到一个大小为 $n \times r$ 的矩阵。

$ \begin{pmatrix} 1 & 2 & 3 & 4\\\ 5 & 6 & 7 & 8 \end{pmatrix} \begin{pmatrix} 1 & 2 & 3\\\ 4 & 5 & 6\\\ 7 & 8 & 9\\\ 10 & 11 & 12 \end{pmatrix} = \begin{pmatrix} 70 & 80 & 90\\\ 158 & 184 & 210 \end{pmatrix} $

如果第一个矩阵的列数不等于第二个矩阵的行数，他们就无法相乘。

试一试：$A={\color{Blue} {\begin{bmatrix} 3 & 1 & -1\\\ 2 & 0 & 3 \end{bmatrix}}}$，$B={\color{Blue} {\begin{bmatrix} 1 & 6\\\ 3 & -5\\\ -2 & 4 \end{bmatrix}}}$，求 $AB$ 和 $BA$

$ AB = \begin{bmatrix} 8 & 9\\\ -4 & 24 \end{bmatrix} $，$ BA = \begin{bmatrix} 15 & 1 & 17\\\ -1 & 3 & -18\\\ 2 & -2 & 14 \end{bmatrix} $

矩阵乘法 ${\color{Red} {不满足}}$ 交换律！

代码实现

给定一个大小为 $n \times m$ 的矩阵 $A[n][m]$ 和一个大小为 $m \times r$ 的矩阵 $B[m][r]$

vector<vector<mint>> matmul(vector<vector<mint>>& A, vector<vector<mint>>& B) {
    int n = A.size();
    int m = A[0].size();
    int r = B[0].size();
    vector C(n, vector<mint>(r));
    rep(i, n)rep(j, m)rep(k, r) C[i][k] += A[i][j] * B[j][k];
    return C;
}

时间复杂度：$O(n^3)$

矩阵乘法快速幂

矩阵幂求和

分析：

注意到，矩阵乘法也是具有结合律和乘法分配律的。
因此：

$A+A^2 = A(I+A)$
$A+A^2+A^3+A^4 = (A+A^2)(I+A^2)$

我们记 ${\rm sum}(n) = A+A^2+\cdots + A^n$
如果 $n$ 是偶数：
$$ {\rm sum}(n) = {\rm sum}(\frac{n}{2})(I+A^{\frac{n}{2}}) $$

如果 $n$ 是奇数：

$$ \begin{align} {\rm sum}(n) &= {\rm sum}(n-1) + A^n \\\ &= {\rm sum}(\frac{n-1}{2})(I + A^{\frac{n-1}{2}}) + A^n \end{align} $$

只需要解决如何快速求 $A^n$

对于整数的幂次，我们可以用快速幂来求
对于矩阵的幂次，我们也可以用快速幂来求
需要注意的是，初始值要设置为单位矩阵 $I$，也就是 $A^0$

代码实现：

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using std::cin;
using std::cout;
using std::vector;
using ll = long long;

int m;

vector<vector<ll>> matadd(vector<vector<ll>> A, vector<vector<ll>> B) {
    int n = A.size();
    vector C(n, vector<ll>(n));
    rep(i, n)rep(j, n) {
        C[i][j] = A[i][j] + B[i][j];
        C[i][j] %= m;
    }
    return C;
}

vector<vector<ll>> matmul(vector<vector<ll>> A, vector<vector<ll>> B) {
    int n = A.size();
    vector C(n, vector<ll>(n));
    rep(i, n)rep(j, n)rep(k, n) {
        C[i][k] += A[i][j] * B[j][k];
        C[i][k] %= m;
    }
    return C;
}

vector<vector<ll>> matexp(vector<vector<ll>> A, ll b) {
    int n = A.size();
    vector Z(n, vector<ll>(n));
    rep(i, n) Z[i][i] = 1;
    while (b > 0) {
        if (b & 1) Z = matmul(Z, A);
        A = matmul(A, A);
        b /= 2;
    }
    return Z;
}

vector<vector<ll>> sum(vector<vector<ll>>& A, int k) {
    if (k == 1) return A;
    int n = A.size();
    vector Z(n, vector<ll>(n));
    rep(i, n) Z[i][i] = 1;
    Z = matadd(Z, matexp(A, k>>1));
    Z = matmul(Z, sum(A, k>>1));
    if (k & 1) Z = matadd(Z, matexp(A, k));
    return Z;
}

int main() {
    int n, k;
    cin >> n >> k >> m;

    vector A(n, vector<ll>(n));
    rep(i, n)rep(j, n) cin >> A[i][j];

    A = sum(A, k);

    rep(i, n)rep(j, n) cout << A[i][j] << " \n"[j == n-1];

    return 0;
}

每次矩阵乘法需要 $O(n^3)$
矩阵快速幂需要 $O(n^3\log k)$
再加上求 ${\rm sum}$ 的分治复杂度，总的时间复杂度是 $O(n^3\log^2 k)$

矩阵乘法优化递推

斐波那契

给一个递推式 $F_n = F_{n-1} + F_{n-2}$，朴素的计算它是线性的。
看一看矩阵在其中能起到什么样的作用呢？

$$ \begin{bmatrix} 1 & 1\\\ 1 & 0 \end{bmatrix} \begin{bmatrix} F_{n-1}\\\ F_{n-2} \end{bmatrix} = \begin{bmatrix} F_n\\\ F_{n-1} \end{bmatrix} $$

我们只要计算这个转移矩阵 $\begin{bmatrix} 1 & 1\\\ 1 & 0 \end{bmatrix}$ 的 $n-1$ 次幂就可以了。

C++ 代码

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using std::cin;
using std::cout;
using std::vector;
using ll = long long;

vector<vector<ll>> matmul(vector<vector<ll>> A, vector<vector<ll>> B) {
    int n = A.size();
    vector<vector<ll>> C(n, vector<ll>(n));
    rep(i, n)rep(j, n)rep(k, n) {
        C[i][k] += A[i][j] * B[j][k];
        C[i][k] %= 10000;
    }
    return C;
}

vector<vector<ll>> matexp(vector<vector<ll>> A, ll b) {
    int n = A.size();
    vector<vector<ll>> Z(n, vector<ll>(n));
    rep(i, n) Z[i][i] = 1;
    while (b > 0) {
        if (b & 1) Z = matmul(Z, A);
        A = matmul(A, A);
        b /= 2;
    }
    return Z;
}

int main() {
    int n;
    while (cin >> n, n != -1) {
        if (n == 0) puts("0");
        else if (n == 1) puts("1");
        else {
            vector A(2, vector<ll>(2));
            A[0][0] = A[0][1] = A[1][0] = 1;

            A = matexp(A, n-1);

            cout << A[0][0] << '\n';
        }
    }

    return 0;
}

【模板】矩阵加速（数列）

我们可以凑

$ \begin{bmatrix} a_n\\\ a_{n-1}\\\ a_{n-2} \end{bmatrix} = \begin{bmatrix} 1 & 0 & 1\\\ 1 & 0 & 0\\\ 0 & 1 & 0 \end{bmatrix}\begin{bmatrix} a_{n-1}\\\ a_{n-2}\\\ a_{n-3} \end{bmatrix} $

于是可以得到

$ \begin{bmatrix} a_n\\\ a_{n-1}\\\ a_{n-2} \end{bmatrix} = \begin{bmatrix} 1 & 0 & 1\\\ 1 & 0 & 0\\\ 0 & 1 & 0 \end{bmatrix}^{n-2}\begin{bmatrix} a_{2}\\\ a_{1}\\\ a_{0} \end{bmatrix} $

C++ 代码

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using std::cin;
using std::cout;
using std::istream;
using std::ostream;
using std::vector;
using ll = long long;

//const int mod = 998244353;
const int mod = 1000000007;
struct mint {
    ll x;
    mint(ll x=0):x((x%mod+mod)%mod) {}
    mint operator-() const {
        return mint(-x);
    }
    mint& operator+=(const mint a) {
        if ((x += a.x) >= mod) x -= mod;
        return *this;
    }
    mint& operator-=(const mint a) {
        if ((x += mod-a.x) >= mod) x -= mod;
        return *this;
    }
    mint& operator*=(const mint a) {
        (x *= a.x) %= mod;
        return *this;
    }
    mint operator+(const mint a) const {
        return mint(*this) += a;
    }
    mint operator-(const mint a) const {
        return mint(*this) -= a;
    }
    mint operator*(const mint a) const {
        return mint(*this) *= a;
    }
    mint pow(ll t) const {
        if (!t) return 1;
        mint a = pow(t>>1);
        a *= a;
        if (t&1) a *= *this;
        return a;
    }

    // for prime mod
    mint inv() const {
        return pow(mod-2);
    }
    mint& operator/=(const mint a) {
        return *this *= a.inv();
    }
    mint operator/(const mint a) const {
        return mint(*this) /= a;
    }
};
istream& operator>>(istream& is, mint& a) {
    return is >> a.x;
}
ostream& operator<<(ostream& os, const mint& a) {
    return os << a.x;
}

vector<vector<mint>> matmul(vector<vector<mint>>& A, vector<vector<mint>>& B) {
    int n = A.size();
    vector C(n, vector<mint>(n));
    rep(i, n)rep(j, n)rep(k, n) C[i][k] += A[i][j] * B[j][k];
    return C;
}

vector<vector<mint>> matexp(vector<vector<mint>>& A, ll b) {
    int n = A.size();
    vector Z(n, vector<mint>(n));
    rep(i, n) Z[i][i] = 1;
    while (b > 0) {
        if (b & 1) Z = matmul(Z, A);
        A = matmul(A, A);
        b /= 2;
    }
    return Z;
}

int main() {
    int t;
    cin >> t;

    while (t--) {
        ll n;
        cin >> n;

        if (n <= 3) puts("1");
        else {
            vector A(3, vector<mint>(3));
            A[0][0] = A[0][2] = A[1][0] = A[2][1] = 1;

            A = matexp(A, n-2);

            mint ans = A[0][0] + A[0][1];
            cout << ans.x << '\n';
        }
    }

    return 0;
}

如果是 $F_n = aF_{n-1} + bF_{n-2} + cF_{n-3}$ 呢？

构造 $\begin{bmatrix} a & b & c\\\ 1 & 0 & 0\\\ 0 & 1 & 0 \end{bmatrix}\begin{bmatrix} F_{n-1}\\\ F_{n-2}\\\ F_{n-3} \end{bmatrix}=\begin{bmatrix} F_{n}\\\ F_{n-1}\\\ F_{n-2} \end{bmatrix}$

广义斐波那契数列

构造 $ \begin{bmatrix} a_n\\\ a_{n-1} \end{bmatrix} = \begin{bmatrix} p & q\\\ 1 & 0 \end{bmatrix} \begin{bmatrix} a_{n-1} \\\ a_{n-2} \end{bmatrix} $

C++ 代码

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using std::cin;
using std::cout;
using std::vector;
using ll = long long;

int m;

vector<vector<ll>> matmul(vector<vector<ll>> A, vector<vector<ll>> B) {
    int n = A.size();
    vector<vector<ll>> C(n, vector<ll>(n));
    rep(i, n)rep(j, n)rep(k, n) {
        C[i][k] += A[i][j] * B[j][k];
        C[i][k] %= 10;
    }
    return C;
}

vector<vector<ll>> matexp(vector<vector<ll>> A, int b) {
    int n = A.size();
    vector<vector<ll>> Z(n, vector<ll>(n));
    rep(i, n) Z[i][i] = 1;
    while (b > 0) {
        if (b & 1) Z = matmul(Z, A);
        A = matmul(A, A);
        b /= 2;
    }
    return Z;
}

int main() {
    int p, q, a1, a2, n;
    cin >> p >> q >> a1 >> a2 >> n >> m;

    vector A(2, vector<ll>(2));
    A[0][0] = p; A[0][1] = q; A[1][0] = 1;

    A = matexp(A, n-2);

    ll ans = A[0][0] * a2 + A[0][1] * a1;
    ans %= m;
    cout << ans << '\n';

    return 0;
}

如果是 $F_n = F_{n-1} + F_{n-2}$，但是让你求 $F_1 + F_2 + \cdots + F_n$ 呢？

记 $S_n = F_1 + F_2 + \cdots + F_n$

构造 $ \begin{bmatrix} F_n \\\ F_{n-1} \\\ S_n \end{bmatrix} = \begin{bmatrix} 1 & 1 & 0\\\ 1 & 0 & 0\\\ 1 & 1 & 1 \end{bmatrix}\begin{bmatrix} F_{n-1} \\\ F_{n-2} \\\ S_{n-1} \end{bmatrix} $

如果是 $F_n = F_{n-1} + F_{n-2}$，但是让你求 $F_1^2 + F_2^2 + \cdots + F_n^2$ ？

记 $S_n = \sum\limits_{i=1}^n F_i^2$
$ \begin{align} S_n & = S_{n-1}+F_n^2\\\ & = S_{n-1} + (F_{n-1} + F_{n-2})^2\\\ & = S_{n-1} + F_{n-1}^2 + F_{n-2}^2 + 2F_{n-1}F_{n-2} \end{align} $

构造 $ \begin{bmatrix} F_n\\\ F_{n-1}\\\ F_n^2\\\ F_{n-1}^2\\\ F_nF_{n-1}\\\ S_n \end{bmatrix} = \begin{bmatrix} 1 & 1 & 0 & 0 & 0 & 0\\\ 1 & 0 & 0 & 0 & 0 & 0\\\ 0 & 0 & 1 & 1 & 2 & 0\\\ 0 & 0 & 1 & 0 & 0 & 0\\\ 0 & 0 & 1 & 0 & 1 & 0\\\ 0 & 0 & 1 & 1 & 2 & 1 \end{bmatrix}\begin{bmatrix} F_{n-1}\\\ F_{n-2}\\\ F_{n-1}^2\\\ F_{n-2}^2\\\ F_{n-1}F_{n-2}\\\ S_{n-1} \end{bmatrix} $

例题： Cellular Automaton

有 $n$ 个数排成一个环。
定义一次变换为：把这个数变成距离它不超过 $d$ 的位置上的数之和对 $m$ 取模的值。
问这样变换 $k$ 次后，每个位置上的数是多少。
$n \leqslant 500$，$m \leqslant 10^9$，$k \leqslant 10^9$

分析：

对于每一次变换，其实可以写成一个矩阵：
比如题中 $d=1$

矩阵 $A=\begin{bmatrix} 1 & 1 & 0 & 0 & 1\\\ 1 & 1 & 1 & 0 & 0\\\ 0 & 1 & 1 & 1 & 0\\\ 0 & 0 & 1 & 1 & 1\\\ 1 & 0 & 0 & 1 & 1 \end{bmatrix}$

但是这么做时间复杂度是 $O(n^3\log k)$
不能通过。
我们可以看看 $A$ 的幂次长什么样

$ A^2=\begin{bmatrix} 3 & 2 & 1 & 1 & 2\\\ 2 & 3 & 2 & 1 & 1\\\ 1 & 2 & 3 & 2 & 1\\\ 1 & 1 & 2 & 3 & 2\\\ 2 & 1 & 1 & 2 & 3 \end{bmatrix} $

$A^3=\begin{bmatrix} 7 & 6 & 4 & 4 & 6\\\ 6 & 7 & 6 & 4 & 4\\\ 4 & 6 & 7 & 6 & 4\\\ 4 & 4 & 6 & 7 & 6\\\ 6 & 4 & 4 & 6 & 7 \end{bmatrix}$

可以发现 $A$ 的幂次都满足 $A[i][j] = A[i-1][j-1]$
因为如果 $A$ 和 $B$ 都满足 $A[i][j] = A[i-1][j-1]$，$B[i][j] = B[i-1][j-1]$
那么

$ \begin{align} C[i][j] & = \sum A[i][k]\ast B[k][j] \\\ & = \sum A[i-1][k-1] \ast B[k-1][j-1] \\\ & = \sum A[i-1][k] \ast B[k][j-1] \\\ & = C[i-1][j-1] \end{align} $

因此一个矩阵只要存下第一行就可以得到整个矩阵。
计算矩阵乘法的时候，只要枚举 $n^2$ 次。
时间复杂度变成了 $O(n^2\log k)$

C++ 代码：

#include <iostream>
#include <vector>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using std::cin;
using std::cout;
using std::vector;
typedef long long ll;

int n, m, d, k;

vector<ll> mul(vector<ll>& a, vector<ll>& b) {
    vector<ll> c(n);
    rep(i, n)rep(j, n) {
        c[i] += a[j] * b[(i-j+n)%n];
        c[i] %= m;
    }
    return c;
}

int main() {
    cin >> n >> m >> d >> k;

    vector<ll> b(n);
    rep(i, n) cin >> b[i];

    vector<ll> a(n);
    a[0] = 1;
    for (int i = 1; i <= d; ++i) a[i] = a[n-i] = 1;

    vector<ll> c(n);
    c[0] = 1;
    while (k) {
        if (k & 1) c = mul(c, a);
        a = mul(a, a);
        k >>= 1;
    }
    c = mul(c, b);

    rep(i, n) cout << c[i] << ' ';

    return 0;
}