数组模拟(静态链表)
- 使用数组模拟可以提高效率,指针+结构体的实现方式每次创建一个新链表时都要
new Node();,此操作很慢,容易超时,所以处于效率考虑,写笔试题一般不采用这种动态链表的方式。可以通过直接初始化n个Node进行改进,但是那种方式本质就和数组模拟(静态链表)差不多。
单链表 & 邻接表
-
单链表最主要用途是写邻接表,邻接表其实是n个链表,最主要的应用是存储图和树,比如最短路问题,最小生成树,最大流问题都是邻接表存储。
-
结构:head -> # -> # -> # -> 0
-
需要定义:value -
e[N], *next ->ne[N], 通过下标进行关联
#include <iostream>
using namespace std;
const int N = 100010;
// head 表示头节点下标
// e[i] 表示节点i的值
// ne[i] 表示节点i的next指针是多少
// idx 存储当前已经用到了哪个点
int head, e[N], ne[N], idx;
// 初始化
void init()
{
head = -1;
idx = 0;
}
// 将x插到头节点
void add_to_head(int x)
{
e[idx] = x;
// idx指向head原本指向的值
ne[idx] = head;
// head指向idx
head = idx;
// idx节点已被使用
idx++;
}
// 将x插入到下标为k的点后面
void add(int k, int x)
{
e[idx] = x;
ne[idx] = ne[k];
ne[k] = idx;
idx++;
}
// 将下标为k的点后面的点删掉
void remove(int k)
{
ne[k] = ne[ne[k]];
}
双链表
-
主要用来优化某些问题
-
实现细节:
-
不定义head和tail,让下标0的点作为最左边的点head,下标1的点为最右边的点tail。
-
l[N]储存每个点左边的点,r[N]储存右边的点。
#include <iostream>
using namespace std;
const int N = 100010;
int m;
int e[N], l[N], r[N], idx;
void init()
{
// 0表示左端点,1表示右端点
r[0] = 1, l[1] = 0;
// 0和1被占用了
idx = 2;
}
// 在第k个点右边插入x
// add(l[k], x)可以在k的左边插入x
void add(int x, int k)
{
e[idx] = x;
r[idx] = r[k];
l[idx] = k;
l[r[k]] = idx;
r[k] = idx;
}
// 删除第k个点
void remove(int k)
{
r[l[k]] = r[k];
l[r[k]] = l[k];
}
动态链表
-
引入:怎样用程序设计语言表示一元多项式,并使其可以进行相加相减相乘运算?
关键数据:项数n,各项系数ai , 指数i -
顺序储存结构直接表示:
数组各分量对应多项式各项 a[i]:项xi的系数ai

-
顺序储存结构表示非0项:
可以用结构数组

-
链表结构储存非0项:
包括系数和指数两个数据以及一个指针域
| coef | expon | link |
|---|---|---|
| 系数 | 指数 | 指针域 |
typedef struct PolyNode *Polynomial;
struct PolyNode
{
int coef;
int expon;
Polynomial link;
};
例如以上两个多项式可以用表示为

定义
线性表是由同类型数据元素构成有序序列的线性结构
- 表中元素个数->长度 起始位置->表头 结束位置->表尾
抽象数据类型描述
-
数据对象集:由n个元素构成的有序序列
-
操作集:
List MakeEmpty();//初始化一个空表L
ElementType FindKth(int K,List L);//根据位序K,返回相应元素
int Find(ElementType X, List L);//在L中查找X第一次出现位置
void Insert(ElementType X ,int i, List L );//在位序i前插入一个新元素X
void Delete(int i,List L);//删除指定位序i - 1的元素
int Length(List L);//返回长度n
如何存储->实现功能?
1.利用数组的连续储存空间顺序存放线性表各元素

List MakeEmpty()
{
List PtrL;
PtrL = (List)malloc(sizeof(struct LNode));
PtrL -> Last = -1;
return PtrL;
}
int Find(ElementType X , List PtrL)
{
int i = 0;
while (i <= PtrL->Last && PtrL ->Data[i] != X)
i++;
if(i > PtrL->Last) return -1;//没找到返回-1
else return i;//找到返回储存位置
}
//插入:把i-1后的元素全部向后挪一位(从后往前)->循环
int Insert(ElementType X ,int i, List PtrL)
{
int j;
if(PtrL->Last == MAXSIZE - 1)
{
printf("FULL"); //表空间已满,无法插入
return;
}
if(i<1 || PtrL -> Last + 2)
{
printf("POSITION INVALID");//插入位置不合法
return;
}
for(j=PtrL->Last;j>=i-1;j--)
PtrL -> Data[j+1] = PtrL -> Data[j];//将ai到an倒序向后移动
PtrL -> Data[i-1] = X;//插入新元素
PtrL -> Last;//Last仍指向最后元素
return;
}
//删除:把i后面的元素依次向前挪
void Delete(int i, List PtrL)
{
int j;
if(i<1 || i>PtrL->Last+1)
{
printf("THIS ELEMENT DO NOT EXIST");
return;
}
for(j=i;j<=PtrL->Last;j++)
PtrL->Data[j-1] = PtrL->Data[j];//顺序前移
PtrL -> Last--;//Last仍指向最后元素
return;
}
2.链式储存实现

//求表长 ->链表遍历
int Length(List PtrL)
{
List p = PtrL;//临时指针p指向链表第一个结点
int j = 0;
while(p)//p指针不为NULL则一直循环
{
p = p->Next;
j++; //当前p指向第j个结点
}
return j;
}
//按序号查找
List FindKth (int K,List PtrL)
{
List p = PtrL;
int i = 1;//i表示第几个元素
while(p != NULL && i<K)
{
p=p->Next;
i++;
}
if(i==K) return p;//找到第K个,返回指针
else return NULL;
}
//按值查找
List Find (ElementType X,List PtrL)
{
List p = Ptrl;
while(p!=PtrL && p->Data!=X)
p=p->Next;
return p;
}
//插入:在第i-1(1<=i<=n+1)个结点后插入一个值为X的新结点
/*先构造一个新结点,用s指向;
再找到第i-1个结点,用p指向;
然后修改指针,插入结点 p->Next=s; s->Next=p->Next;*/
List Insert(ELementType X,int i,List PtrL)
{
List p,s;
if(i==1)//新结点插入在表头
{
s=(List)malloc(sizeof(struct LNode));//申请,填装结点
s->Data = X;
s->Next = PtrL;
return s;//返回新表头指针
}
p=FindKth(i-1.PtrL);//查找第i-1个结点
if(p==NULL)
{
printf("参数i错");
return NULL;
}
else{
s=(List)malloc(sizeof(struct LNode));
s->Data = X;
s->Next = p->Next;
p->Next = s;
return PtrL;
}
}
//删除第i个位置上的结点
//用p指针指向第i-1个结点 s=p->Next; p->Next = s->Next; free(s);
List Delete(int i,List PtrL)
{
List p,s;
if(i==1)//删除头结点
{
s=PtrL;//s指向第一个结点
if(PtrL!=NULL) PtrL=PtrL->Next;//从链表中删除
else return NULL;
flee(s);
return PtrL;
}
p = FindKth(i-1,PtrL)//查找第i-1个结点
if(p==NULL)
{
printf("第%d个结点不存在",i-1); return NULL;
}
else if(p->Next == NULL)
{
printf("第%d个结点不存在",i); return NULL;
}
else
{
s=p->Next;//s指向第i个结点
p->Next = s->Next;//从链表删除
free(s);//释放被删除结点
return PtrL;
}
}
例题
- Acwing#28
给定单向链表的一个节点指针,定义一个函数在O(1)时间删除该结点。
假设链表一定存在,并且该节点一定不是尾节点。
- 样例:
输入:链表 1->4->6->8
删掉节点:第2个节点即6(头节点为第0个节点)
输出:新链表 1->4->8
- 题解:
由于是单链表,不能找到前驱节点,所以不能按常规方法将该节点删除。可以将下一个节点的值复制到当前节点,然后将下一个节点删除即可。
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
void deleteNode(ListNode* node) {
node->val = node->next->val;
node->next = node->next->next;
}
};
2.AcWing#36
输入两个递增排序的链表,合并这两个链表并使新链表中的结点仍然是按照递增排序的。
- 样例:
输入:1->3->5 , 2->4->5
输出:1->2->3->4->5->5
- 题解:其实在考归并算法,可以用两个指针分别指向两个链表的头节点,把每次指向的两个结点中比较小的放在答案里。
/*
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode* merge(ListNode* l1, ListNode* l2)
{
// 创建虚拟头节点
auto dummy = new ListNode(-1);
// cur指针记录当前链表尾节点
auto cur = dummy;
// 两个指针非空就一直遍历
while (l1 && l2)
{
if(l1->val < l2->val)
{
cur->next = l1;
cur = l1;
l1 = l1->next;
}
else
{
cur->next = l2;
cur=l2;
l2 = l2->next;
}
}
if(l1) cur->next = l1;
else cur->next = l2;
return dummy->next;
}
};
3.AcWing#35
定义一个函数,输入一个链表的头结点,反转该链表并输出反转后链表的头结点。
- 样例:
输入:1->2->3->4->5->NULL
输出:5->4->3->2->1->NULL
- 题解:
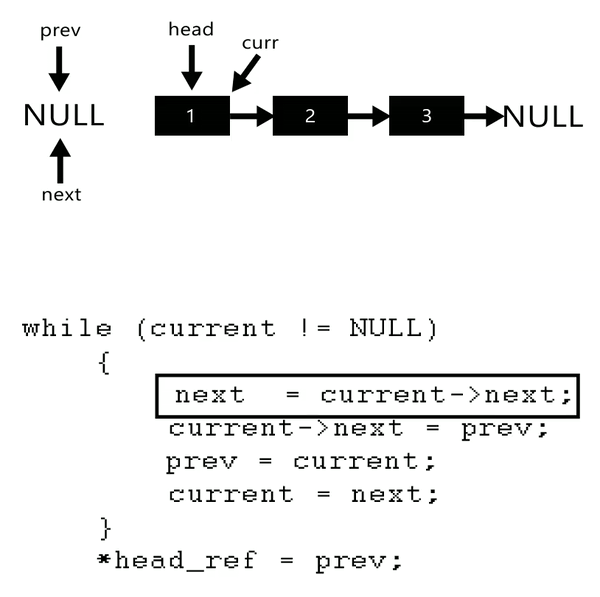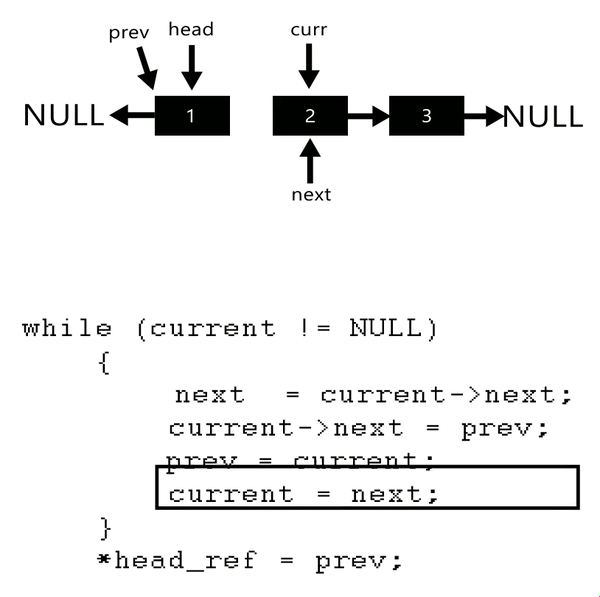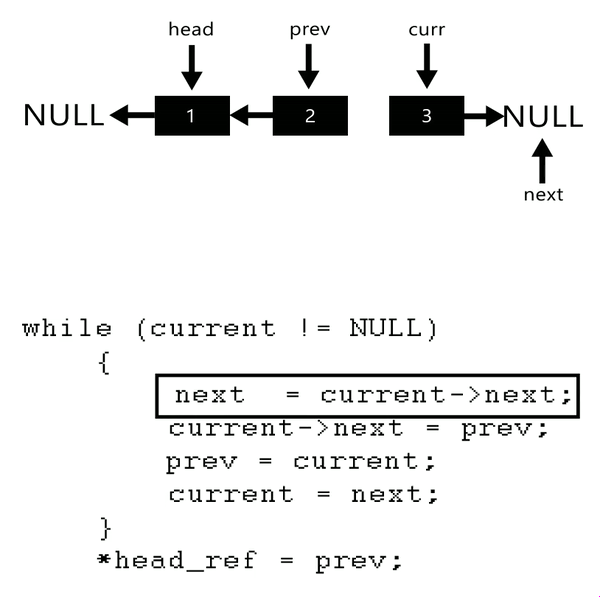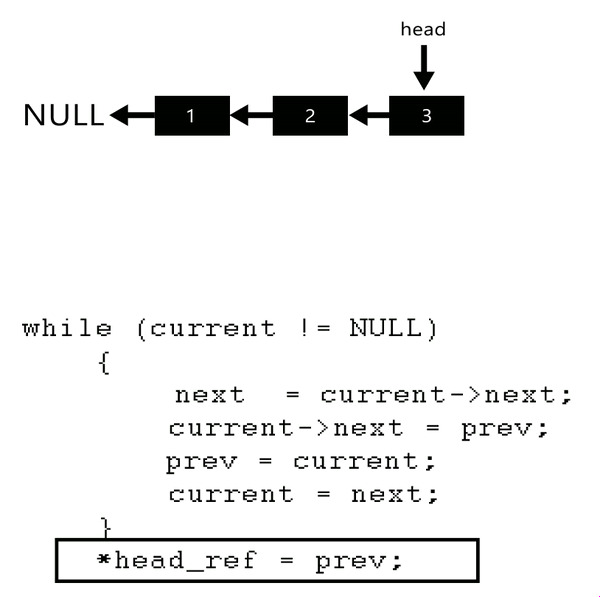
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode* reverseList(ListNode* head) {
// 记录前驱结点
ListNode* pre = nullptr;
auto cur = head;
while(cur)
{
auto next = cur->next;
cur->next = pre;
pre = cur;
cur = next;
}
return pre;
}
};
- 包含IO:
// 迭代做法
// Iterative C++ program to reverse
// a linked list
#include <iostream>
using namespace std;
/* Link list node */
struct Node {
int data;
struct Node* next;
Node(int data)
{
this->data = data;
next = NULL;
}
};
struct LinkedList {
Node* head;
LinkedList()
{
head = NULL;
}
/* Function to reverse the linked list */
void reverse()
{
// Initialize current, previous and
// next pointers
Node* current = head;
Node *prev = NULL, *next = NULL;
while (current != NULL) {
// Store next
next = current->next;
// Reverse current node's pointer
current->next = prev;
// Move pointers one position ahead.
prev = current;
current = next;
}
head = prev;
}
/* Function to print linked list */
void print()
{
struct Node* temp = head;
while (temp != NULL) {
cout << temp->data << " ";
temp = temp->next;
}
}
void push(int data)
{
Node* temp = new Node(data);
temp->next = head;
head = temp;
}
};
/* Driver program to test above function*/
int main()
{
/* Start with the empty list */
LinkedList ll;
ll.push(20);
ll.push(4);
ll.push(15);
ll.push(85);
cout << "Given linked list\n";
ll.print();
ll.reverse();
cout << "\nReversed Linked list \n";
ll.print();
return 0;
}
广义表
- 如何表示二元多项式?

1.广义表是线性表的推广
2.对于线性表而言,n个元素都是基本的单元素,广义表中,这些元素不仅可为单元素也可以是另一个广义表
typedef struct GNode *GList;
struct GNode
{
int Tag; //标志域,0表示结点为单元素,1表示结点为广义表
union{ //子表指针域Sublist与banyans数据域Data复用,共用存储空间
ElementType Data;
GList SubList;
}URegion;
GList Next; //指向后继结点
}
| Tag | Data | Next |
|---|---|---|
| SubList |
- 多重链表:链表结点可能同时隶属于多条链
1.多重链表指针域有多个,比如前例包含了Next和SubLIst两个指针域, 反之不一定正确,比如双向链表不是多重链表
2.树,图等复杂数据结构可以采用多重链表方式实现存储


Term表示稀疏矩阵中非0元素结点,Head为头结点(标识域Tag区分)
左上角Term为入口结点,表示有四行五列,非0项共7项

Con - 线性表定义与操作-顺序表
typedef int Position;
typedef struct LNode *List;
struct LNode {
ElementType Data[MAXSIZE];
Position Last;
};
/* 初始化 */
List MakeEmpty()
{
List L;
L = (List)malloc(sizeof(struct LNode));
L->Last = -1;
return L;
}
/* 查找 */
#define ERROR -1
Position Find( List L, ElementType X )
{
Position i = 0;
while( i <= L->Last && L->Data[i]!= X )
i++;
if ( i > L->Last ) return ERROR; /* 如果没找到,返回错误信息 */
else return i; /* 找到后返回的是存储位置 */
}
/* 插入 */
/*注意:在插入位置参数P上与课程视频有所不同,课程视频中i是序列位序(从1开始),这里P是存储下标位置(从0开始),两者差1*/
bool Insert( List L, ElementType X, Position P )
{ /* 在L的指定位置P前插入一个新元素X */
Position i;
if ( L->Last == MAXSIZE-1) {
/* 表空间已满,不能插入 */
printf("表满");
return false;
}
if ( P<0 || P>L->Last+1 ) { /* 检查插入位置的合法性 */
printf("位置不合法");
return false;
}
for( i=L->Last; i>=P; i-- )
L->Data[i+1] = L->Data[i]; /* 将位置P及以后的元素顺序向后移动 */
L->Data[P] = X; /* 新元素插入 */
L->Last++; /* Last仍指向最后元素 */
return true;
}
/* 删除 */
/*注意:在删除位置参数P上与课程视频有所不同,课程视频中i是序列位序(从1开始),这里P是存储下标位置(从0开始),两者差1*/
bool Delete( List L, Position P )
{ /* 从L中删除指定位置P的元素 */
Position i;
if( P<0 || P>L->Last ) { /* 检查空表及删除位置的合法性 */
printf("位置%d不存在元素", P );
return false;
}
for( i=P+1; i<=L->Last; i++ )
L->Data[i-1] = L->Data[i]; /* 将位置P+1及以后的元素顺序向前移动 */
L->Last--; /* Last仍指向最后元素 */
return true;
}
Con - 线性表定义与操作-链式表
typedef struct LNode *PtrToLNode;
struct LNode {
ElementType Data;
PtrToLNode Next;
};
typedef PtrToLNode Position;
typedef PtrToLNode List;
/* 查找 */
#define ERROR NULL
Position Find( List L, ElementType X )
{
Position p = L; /* p指向L的第1个结点 */
while ( p && p->Data!=X )
p = p->Next;
/* 下列语句可以用 return p; 替换 */
if ( p )
return p;
else
return ERROR;
}
/* 带头结点的插入 */
/*注意:在插入位置参数P上与课程视频有所不同,课程视频中i是序列位序(从1开始),这里P是链表结点指针,在P之前插入新结点 */
bool Insert( List L, ElementType X, Position P )
{ /* 这里默认L有头结点 */
Position tmp, pre;
/* 查找P的前一个结点 */
for ( pre=L; pre&&pre->Next!=P; pre=pre->Next ) ;
if ( pre==NULL ) { /* P所指的结点不在L中 */
printf("插入位置参数错误\n");
return false;
}
else { /* 找到了P的前一个结点pre */
/* 在P前插入新结点 */
tmp = (Position)malloc(sizeof(struct LNode)); /* 申请、填装结点 */
tmp->Data = X;
tmp->Next = P;
pre->Next = tmp;
return true;
}
}
/* 带头结点的删除 */
/*注意:在删除位置参数P上与课程视频有所不同,课程视频中i是序列位序(从1开始),这里P是拟删除结点指针 */
bool Delete( List L, Position P )
{ /* 这里默认L有头结点 */
Position tmp, pre;
/* 查找P的前一个结点 */
for ( pre=L; pre&&pre->Next!=P; pre=pre->Next ) ;
if ( pre==NULL || P==NULL) { /* P所指的结点不在L中 */
printf("删除位置参数错误\n");
return false;
}
else { /* 找到了P的前一个结点pre */
/* 将P位置的结点删除 */
pre->Next = P->Next;
free(P);
return true;
}
}


刚好是我们学校的考研题,mark了
好巧hh