目录
1.
2.
待填写


重新回顾CNN
编码器，
解码器

这里记四周

数组操作np.array 和torch tensor张量，广播机制(很容易犯错的计算时特殊格式复制)，其他和py差不太多，就先不记了。等过两个月用的熟练一些以后再写自己觉得很常用的，以及需要注意的

线性回归和分类

让我们打开同学们的笔记和d2l官网
一阵copy

kaggle 房产价格预测。
因变量$y$ : 房价
自变量$x_i$ 一堆带参数的变量/特征features。
好像是因为有covariance所以也叫covariate?

y^=w^⊤x+b.
加粗表示矩阵/这里是向量

2. 损失函数 loss function

用来量化quantify 目标的实际值和预测值之间的差距。(distance) 残差 。

/方差既视感。

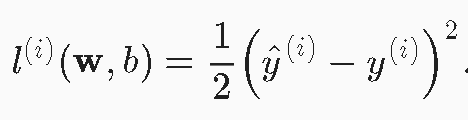
(具体理解要以视频为准 有q&a)

需要n个样本上的损失，取个mean，避免于残差巨巨巨的outlier损失拉升爆表

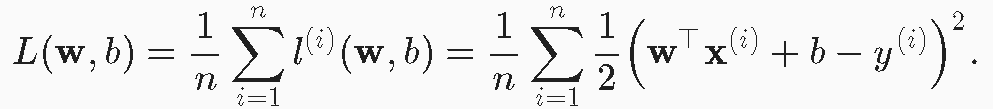
很明显，咱们需要这个差异值最小，即找一组参数使损失min。
w’, b’ = $ \underbrace{argmin}_{w, b}{ L(W, b)}$
Tbc

虽然单层NN（线性回归是有解析解的）， 可以再无法得到解的情况下使用梯度下降gradient descent 逼近局部最优解。

我们通常会在每次需要计算更新的时候随机抽取一小批样本，这种变体叫做小批量随机梯度下降（minibatch stochastic gradient descent）。
用来避免执行缓慢，而遍历整个数据集。

用numpy为基础的torch就不得不说这个矩阵(矢量)加速了，太牛逼了。

f'{timer.stop():.5f} sec'
> 直接秒杀 0.00000000000000000000000000000000000000000000000x 秒

从scratch零实现

#首先排除mxnet
%matplotlib inline # 把这里的函数加成默认
import random #随机初始化用
import torch #
from d2l import torch as d2l

0. 生成数据集

def 生成(w, b, nums):
    torch.normal(0, 1, (nums, len(w))
    torch.matmul(X, w) +b
    ++ torch.normal(0, 0.01, y.shape) #此题error的标准差σ设成0.01。毕竟咋们只是前期入个门
w = torch.tensor([2, -2.6])
y = 4.2
features, labels = 生成(w, b, 1000)
#即特征是个二维数据，标号是一维数据(一个)
print('features:', features[0], '\nlabel:', labels[0]) # 看一看
> features: tensor([blahblah, blahbl] )
> label: tensor([balsdha])

看看散点图

d2l.set_figsize()
d2l.plt.scatter(features[:, (1)].detach().numpy(),
                labels.detach().numpy(), 1);

通用的优化算法：随机梯度下降

在每一步中，使用从数据集中随机抽取的一个小批量，然后根据参数计算损失的梯度。接下来，朝着减少损失的方向更新我们的参数。 下面的函数实现小批量随机梯度下降更新。该函数接受模型参数集合、学习速率和批量大小作为输入。每一步更新的大小由学习速率lr决定。 因为我们计算的损失是一个批量样本的总和，所以我们用批量大小（batch_size）来归一化步长，这样步长大小就不会取决于我们对批量大小的选择。

def sgd(params, lr, batch_size):  #@save
    """小批量随机梯度下降。"""
    with torch.no_grad():
        for param in params:
            param -= lr * param.grad / batch_size
            param.grad.zero_()

卧槽又可以用框架实现了，简直不讲武德

from torch import nn # 即神经网络简写
net = nn.Sequential(nn.Linear(2, 1))
##                  ##
##      初始化      ##
net[0].weight.data.normal_(0, 0.01)
net[0].bias.data.fill_(0)
##  net[0]选择网络中第一个图层. weight.data, bias.data来设置参数(初始值)
##      定义损失函数##
loss = nn.MSELoss()

##      定义优化算法##
trainer = torch.optim.SGD(net.parameters(), lr=0.03)
##      小批量设置lr值为0.03, 优化的参数, 模型中获得即可

##      train!!!    ##
num_epochs = 3
for epoch in range(num_epochs):
    for X, y in data_iter:
        l = loss(net(X), y)
        trainer.zero_grad()
        l.backward()
        trainer.step()
    l = loss(net(features), labels)
    print(f'epoch {epoch + 1}, loss {l:f}')
##                  ##
##      Output      ##
> epoch 1, loss 0.000471
> epoch 2, loss 0.000103
> epoch 3, loss 0.000103

w = net[0].weight.data
print('w的估计误差：', true_w - w.reshape(true_w.shape))
b = net[0].bias.data
print('b的估计误差：', true_b - b)
##                  ##
> w的估计误差： tensor([-0.0004, -0.0005])
> b的估计误差： tensor([-0.0001])

分类！！！Softmax回归

咱们感兴趣的这回是哪一个！！ A 或 B 或。。。

图像分类
等等 实现

多层感知机 Multi-layel perceptron MLP

将许多全连接层堆叠在一起。每一层都输出到上面的层，直到生成最后的输出。
前面那些层是
把最后一层看作线性预测器。

逻辑回归Logistic regression是一种广义的线性回归。glm。（卧槽！）
n个Bernoulli 分布 – Binomial
p.m.f $f(x) 即P(X=k) = {n \choose k} p^k (1-p)^{n-k}$
知识点: Sigmoid函数
$ S(x) = \frac{1}{e^{-x} + 1}$

Sigmoid因为s型特性，所以可以把(-inf, inf)的值映射到(0,1)里。所以叫squashing函数，把大范围用手捏挤进小范围。

话说国内卷不过大家，算法这种天阶内功我就不专门弄了(近两年)，转向面向实际的技能了