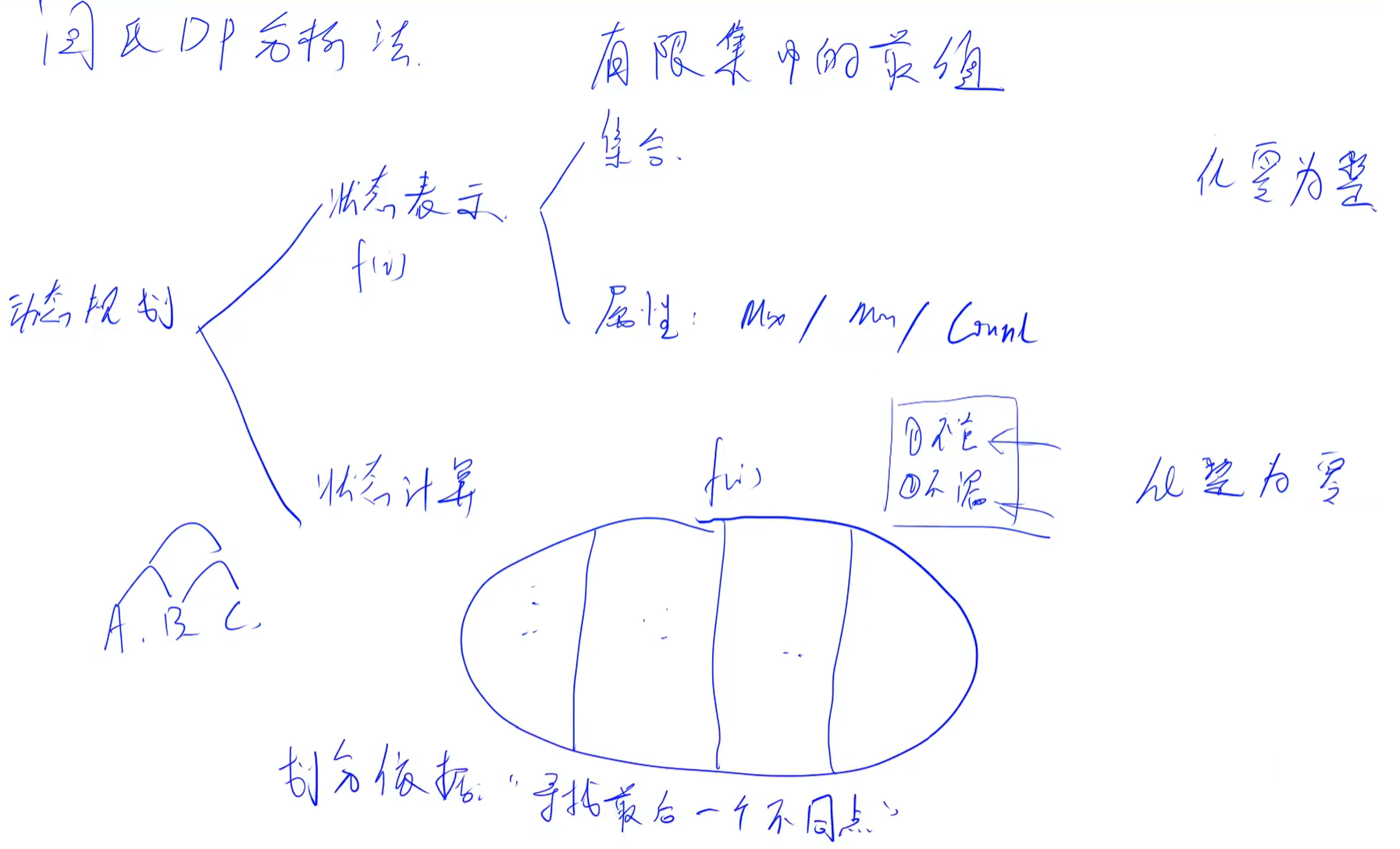
• 闫氏DP分析法：b站讲解

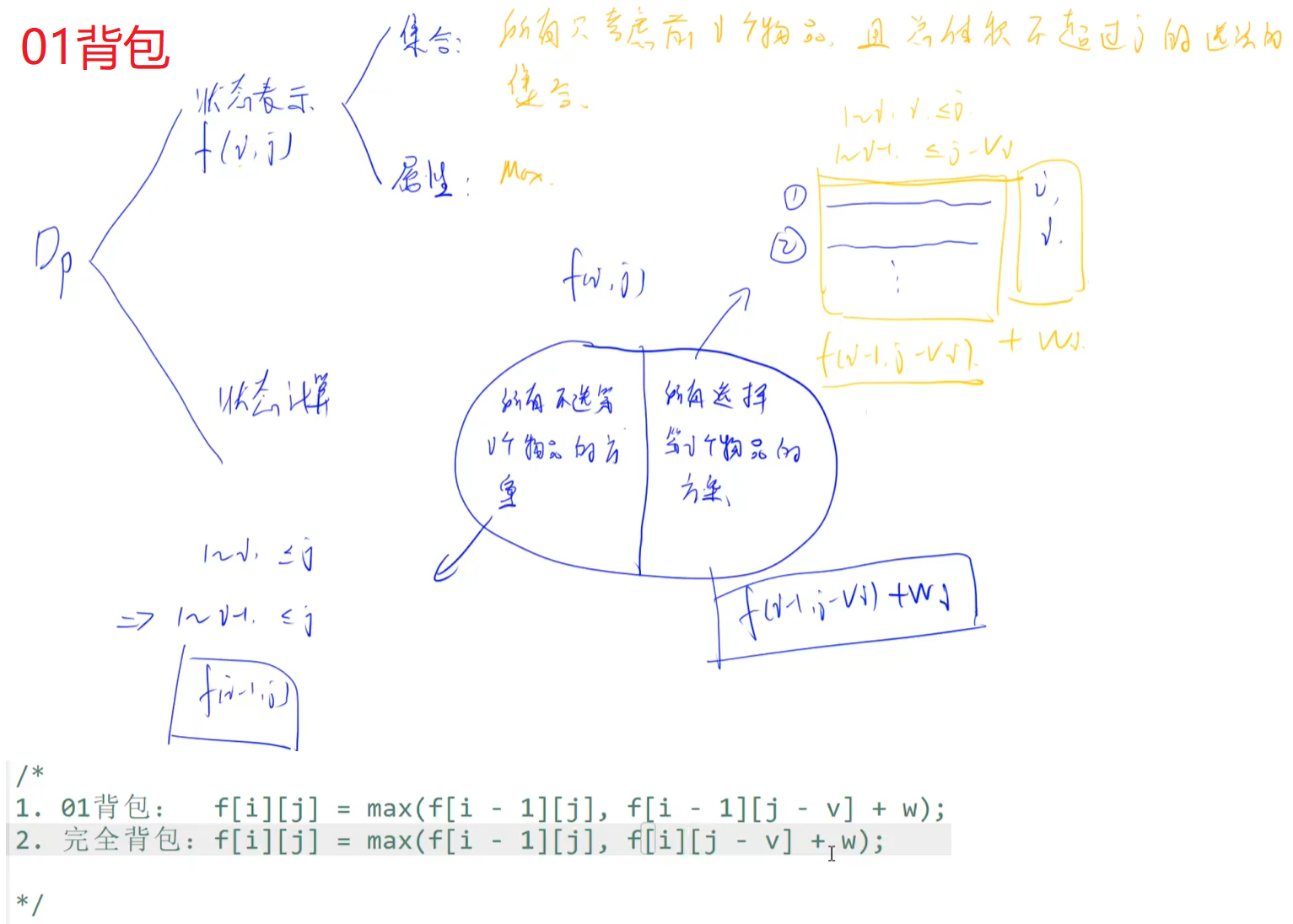
1. 01背包问题：

• y总讲解：b站，题目：算法基础课：AcWing 2. 01背包问题

• 优质题解： 深蓝，shiqumi

1.1 01背包：二维朴素写法

// 01背包：二维朴素写法
#include<iostream>

using namespace std;

const int N = 1010;
int n, m;
int v[N], w[N];
int f[N][N];

int main(){
    cin >> n >> m;
    for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];

    for (int i = 1; i <= n; i ++)
        for (int j = 0; j <= m; j ++ ){ // 01背包 二维 正序/逆序 更新 都可以，完全背包 二维 只能 正序更新
        // for (int j = m; j >= 0; j -- ){ // 01背包 逆序 更新 也可以
            if (j < v[i]) f[i][j] = f[i - 1][j];

            else f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);
            // 完全背包：f[i][j] = max(f[i - 1][j], f[i][j - v[i]] + w[i]);
        }

    cout << f[n][m] << endl;
    return 0;
}

1.2 01背包：二维朴素写法 —> 一维空间优化写法 ：

1.2.1 01背包：二维朴素写法 —> 一维空间优化 讲解：shiqumi

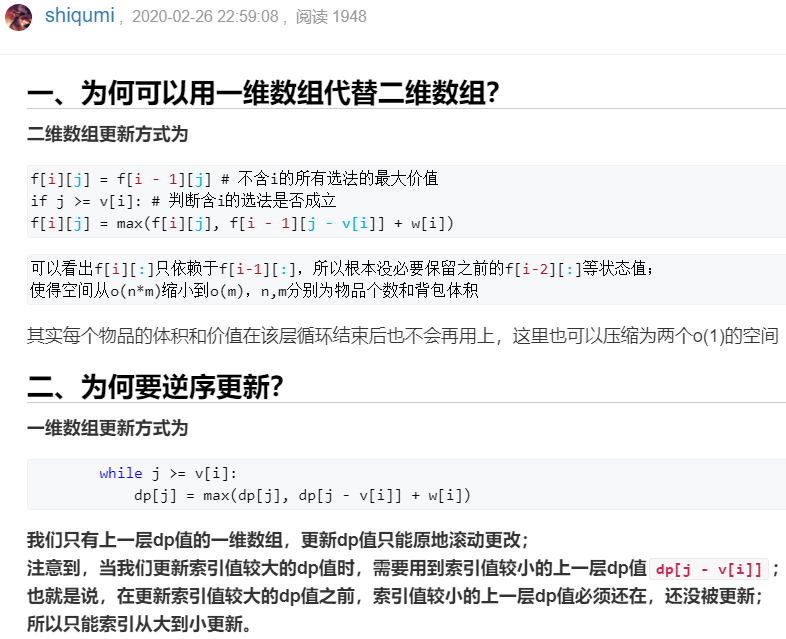
1.2.2 01背包：二维朴素写法 —> 一维空间优化写法 过程展示：

// 01背包：二维朴素写法 ---> 一维空间优化写法 过程展示：
#include<iostream>

using namespace std;

const int N = 1010;
int n, m;
int v[N], w[N];
int f[N];

int main(){
    cin >> n >> m;
    for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];

    for (int i = 1; i <= n; i ++)
        for (int j = m; j >= v[i]; j -- ){ // 01背包 二维 --> 一维后, 只能 逆序 更新
        // for (int j = 0; j <= m; j ++ ){ // 01背包 二维更新，正序 和 逆序 都可以

            if (j < v[i]) f[j] = f[j]; // j < v[i], f[j] = f[j] 是恒等式可以删除
            // f[i][j] = f[i - 1][j]; // 01背包(二维)

            else f[j] = max(f[j], f[j - v[i]] + w[i]);
            // 01背包(二维)：  f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);
            // 完全背包(二维)：f[i][j] = max(f[i - 1][j], f[i][j - v[i]] + w[i]);
        }

    cout << f[m] << endl; // f[n][m] ---> f[m]
    return 0;
}

1.2.3 01背包：二维朴素写法 —> 一维空间优化写法，简化后代码

• 01背包：一维空间优化写法, 将 以上代码 最终简写为如下：（ 注意 for (int j = m; j >= v[i]; j – ) 中 j >= v[i]，简化之前 j >= 0）

// 01背包：一维空间优化写法, 将 以上代码 最终简写为如下：
// 注意 for (int j = m; j >= v[i]; j -- ) 中 j >= v[i]，简化之前 j >= 0
#include<iostream>

using namespace std;

const int N = 1010;
int n, m;
int v[N], w[N];
int f[N];

int main(){
    cin >> n >> m;
    for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];

    for (int i = 1; i <= n; i ++)
        for (int j = m; j >= v[i]; j -- ) // 01背包 一维写法 只能 逆序更新
        // 完全背包 一维写法 只能 正序更新：for (int j = v[i]; j <= m; j ++ )
            f[j] = max(f[j], f[j - v[i]] + w[i]);

    cout << f[m] << endl;
    return 0;
}

1.3 01背包：一维空间优化写法，进一步优化：

• 01背包：一维空间优化写法，进一步优化：int v[N], w[N]; —> int v, w; 因为 v[i] w[i]在当层用完后就用不到了，所以用一个 int型变量 存储即可

// 01背包：一维空间优化写法，进一步优化：int v[N], w[N]; ---> int v, w;
// v[i] w[i]在当层用完后就用不到了，所以用一个int型变量存储即可
#include<iostream>

using namespace std;

const int N = 1010;
int n, m;
int v, w;
int f[N];

int main(){
    cin >> n >> m;

    for (int i = 1; i <= n; i ++){ // 注意加了cin >> v >> w; 之后, 这里有个 大括号
        cin >> v >> w; // 注意 不是在 第二个 for循环里
        for (int j = m; j >= v; j -- ) // 01背包 一维写法 只能 逆序更新
        // 完全背包 一维写法 只能 正序更新：for (int j = v[i]; j <= m; j ++ )
            f[j] = max(f[j], f[j - v] + w);
    }

    cout << f[m] << endl;
    return 0;
}

2. 完全背包

• y总讲解：b站，题目：算法基础课：AcWing 3. 完全背包问题

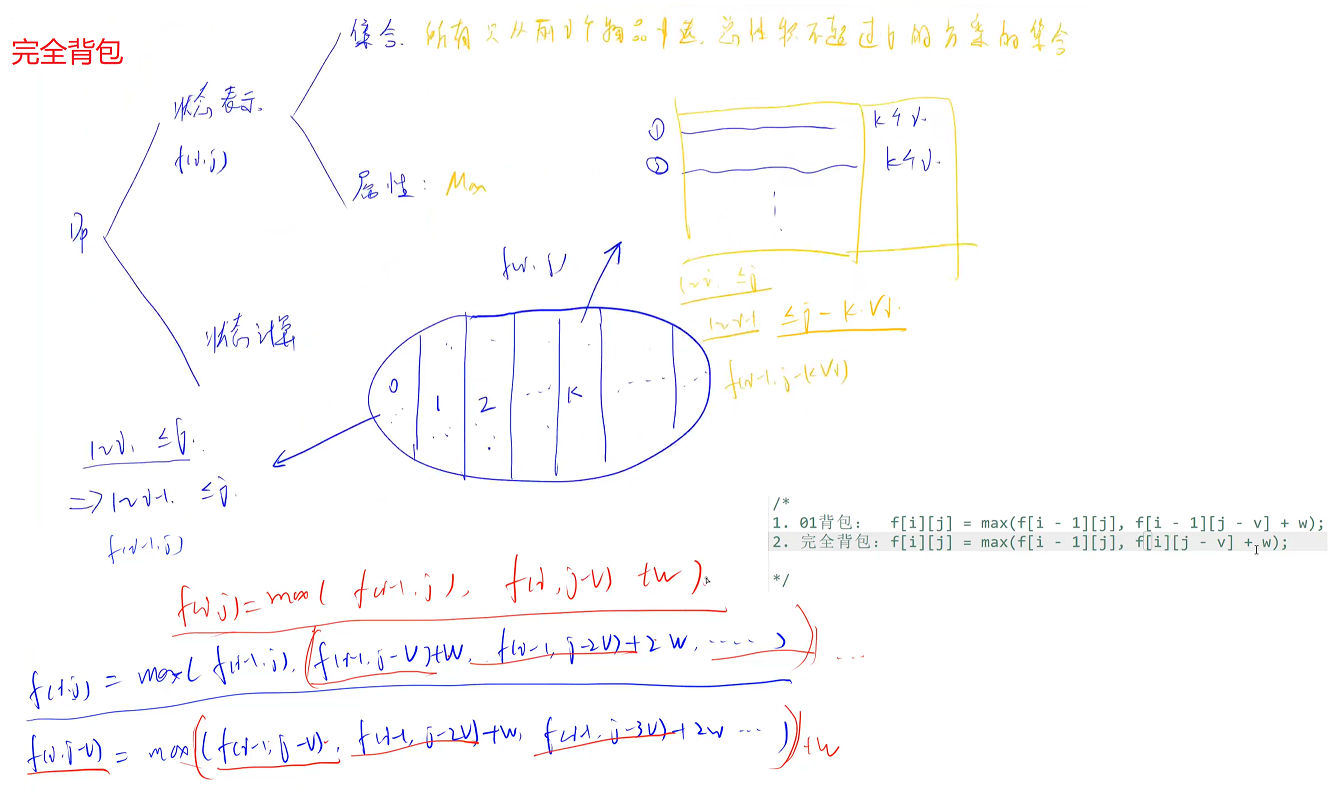
2.1 完全背包：二维朴素写法

// 完全背包：二维朴素写法
#include<iostream>

using namespace std;

const int N = 1010;
int n, m;
int v[N], w[N];
int f[N][N];

int main(){
    cin >> n >> m;
    for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];

    for (int i = 1; i <= n; i ++ )
        for (int j = 0; j <= m; j ++ ){ // 完全背包 二维 只能 正序更新, 01背包 二维 正序/逆序 更新 都可以
        // for (int j = m; j >= 0; j -- ){ // 完全背包 二维 逆序更新 会报错

            if (j < v[i]) f[i][j] = f[i - 1][j];
            else f[i][j] = max(f[i - 1][j], f[i][j - v[i]] + w[i]);
            // 01 背包：f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);
        }

    cout << f[n][m] << endl;
    return 0;
}

• 完全背包二维 之所以只能正序更新，不能逆序更新是因为：$f[i][j] = max(f[i - 1][j], f[i][j - v[i]] + w[i]);$ 想求 $f[i][j]$，要先求$f[i][j - v[i]]$，两者都是f[i]，也就是在同一层，所以只能正序更新。
• 01背包二维之所以 正序逆序都可以是因为：$f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);$，相求$f[i][j]$，要先求$f[i - 1][j - v[i]]$，前者是f[i]，后者是f[i - 1]，不在同一层，所以 正序逆序更新都可以。

2.2 完全背包：二维朴素写法 —> 一维空间优化写法 ：

2.2.1 完全背包：二维朴素写法 —> 一维空间优化写法 过程展示：

// 完全背包：二维朴素写法 ---> 一维空间优化写法 过程展示：
#include<iostream>

using namespace std;

const int N = 1010;
int n, m;
int v[N], w[N];
int f[N];

int main(){
    cin >> n >> m;
    for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];

    for (int i = 1; i <= n; i ++ )
        for (int j = 0; j <= m; j ++ ){ // 完全背包 一维 只能 正序更新
        // 01背包 一维 只能 逆序更新: for (int j = m; j >= v[i]; j -- )

            if (j < v[i]) f[j] = f[j];
            // 完全背包(二维)：f[i][j] = f[i - 1][j];

            else f[j] = max(f[j], f[j - v[i]] + w[i]);
            // 完全背包(二维)：f[i][j] = max(f[i - 1][j], f[i][j - v[i]] + w[i]);
            // 01 背包(二维)： f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);
        }

    cout << f[m] << endl; // f[n][m] ---> f[m]
    return 0;
}

2.2.2 完全背包：二维朴素写法 —> 一维空间优化写法，简化后代码

• 完全背包：一维空间优化写法, 将 以上代码 最终简写为如下：（ 注意 for (int j = v[i]; j <= m; j ++ ) 中j 初始化为 v[j]，简化之前 j 初始化为 0）

// 完全背包：一维空间优化写法, 将 以上代码 最终简写为如下：
// 注意 for (int j = v[i]; j <= m; j ++ ) 中 j 初始化为 v[j]，简化之前 j 初始化为 0
#include<iostream>

using namespace std;

const int N = 1010;
int n, m;
int v[N], w[N];
int f[N];

int main(){
    cin >> n >> m;
    for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];

    for (int i = 1; i <= n; i ++ )
        for (int j = v[i]; j <= m; j ++ ) // 完全背包 一维 只能 正序更新
        // 01背包 一维 只能 逆序更新: for (int j = m; j >= v[i]; j -- )
            f[j] = max(f[j], f[j - v[i]] + w[i]);

    cout << f[m] << endl; // f[n][m] ---> f[m]
    return 0;
}

2.3 完全背包 一维空间优化写法，进一步优化

// 完全背包 一维空间优化写法，进一步优化：int v[N], w[N]; ---> int v, w;
// v[i] w[i]在当层用完后就用不到了，所以用一个int型变量存储即可
#include<iostream>

using namespace std;

const int N = 1010;
int n, m;
int v, w;
int f[N];

int main(){
    cin >> n >> m;

    for (int i = 1; i <= n; i ++ ){ // 注意加了cin >> v >> w; 之后, 这里有个 大括号
        cin >> v >> w; // 注意 不是在 第二个 for循环里
        for (int j = v; j <= m; j ++ ) // 完全背包 一维 只能 正序更新
        // 01背包 一维 只能 逆序更新: for (int j = m; j >= v[i]; j -- )
            f[j] = max(f[j], f[j - v] + w);
    }

    cout << f[m] << endl; // f[n][m] ---> f[m]
    return 0;
}

1