地址 http://poj.org/problem?id=3061

解法1

使用双指针

由于序列是连续正数

使用l r 表示选择的子序列的起始

每当和小于要求的时候 我们向右侧扩展 增大序列和

每当和大于等于要求的时候 我们将子序列左边的数字剔除 看能是在减少长度情况下 还能保持子序列和满足要求

这样在指定起点下的满足要求的最短子序列和都会被记录 然后在比较出最短长度的子序列

如图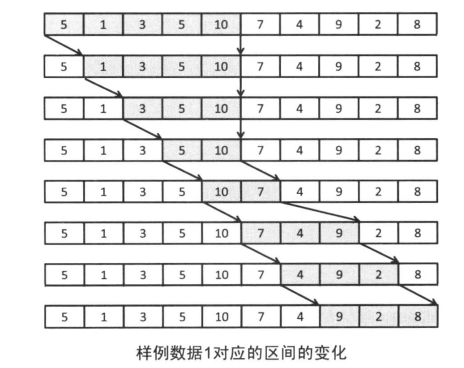

#include <iostream>
#include <vector>
#include <algorithm>
#include <memory.h>
#include <queue>


using namespace std;


/*
Sample Input
6
10 15
5 1 3 5 10 7 4 9 2 8
5 11
1 2 3 4 5
1 2
1
1 1
5
3 9999
1 2 3 
3 0
1 2 3 

Sample Output
2
3
*/
const int MAX_N = 1000010;
int n, m;
int nums[MAX_N];

int ret = MAX_N;

void solve()
{
    int sum = 0;
    int minlen = MAX_N;

    int r = -1; int l = 0;

    while (1) {
        if (sum < m) {
            r++;
            if (r >= n) break;
            sum += nums[r];
        }
        else {
            //sum >= m
            minlen = min(minlen, r - l + 1);
            sum -= nums[l];
            l++;
            if (l >= n) break;
            if (l > r) {
                r = l;
                sum = nums[l];
            }
        }
    }


    if (minlen == MAX_N) minlen = 0;
    cout << minlen << endl;
}


int main()
{
    int loop;
    cin >> loop;
    while (loop--) {
        cin >> n >> m;

        for (int i = 0; i < n; i++) {
            cin >> nums[i];
        }
        ret = MAX_N;
        solve();
    }

    return 0;
}

//=========================================================================================

解法2 二分查找前缀和
使用前缀和就可以快速定位各个子序列的和

然后使用二分查找进行查找以指定索引开始的子序列满足和要求的最短长度

最后得到所有满足需求中最短的子序列长度

代码如下

#include <iostream>
#include <algorithm>

using namespace std;

const int MAX_N = 1000010;
int n, m;
int nums[MAX_N];
int preSum[MAX_N];


int binartSearch(int sum[],int l, int r)
{
    int start = l;
    while (l < r) {
        int mid = (l + r) >> 1;
        if (sum[mid] - sum[start] >= m) {
            r = mid;
        }
        else {
            l = mid + 1;
        }
    }

    return (l-start);
}

int solve()
{
    int     ret = MAX_N;
    for (int i = 1; i <= n; i++) {
        preSum[i] = preSum[i - 1] + nums[i];
    }
    //全部加起来都无法达到标准
    if (preSum[n] < m) return 0;

    for (int i = 1; i < n; i++) {
        //if(preSum[i]+m <= preSum[n]){
        if (preSum[n] - preSum[i] >= m) {
            int idx = binartSearch(preSum,i,n);
            ret = min(ret, idx);
        }
    }

    if (ret == MAX_N) ret = 0;
    return ret;
}


int main()
{
    int loop;
    cin >> loop;

    while (loop--) {
        cin >> n >> m;
        memset(nums,0,sizeof(nums));
        memset(preSum, 0, sizeof(preSum));

        for (int i = 1; i <= n; i++) {
            cin >> nums[i];
        }
        cout << solve() << endl;
    }

    return 0;
}