数论

筛法筛质数

primes数组存储素数，cnt统计素数个数
st判断是否被筛掉

Miller Rabin算法

1. 埃氏筛

2. 时间复杂度O（n lglgn）
   思想就是如果i是质数，那么每次将i的倍数筛去

参考代码

for(int i = 2; i <= n ; i++){
    if(!st[i] ) primes[cnt++] = i ;  //没有被筛掉，说明是一个质数
    else {
        continue ;             //不是质数的不需要再筛，因为已经被该数的素因数筛掉了，如果不加这个优化时间复杂度是O（n lgn）
    }
    for(int j = 2 * i ; j <= n; j += i){
        st[j] = 0 ;
    }
}

1. 线性筛

2. 时间复杂度为线性 O（n）

参考代码

for(int i = 2;  i<= n ; i++){
    if(!st[i]) primes[cnt++] = i;
    for(int j = 0 ; primes[j] * i <= n ; j++){
        st[primes[j] * i ] = 1; 
        if(i % primes[j] == 0 ) break ; 
    }
}

约数
如果 N = p1^c1 * p2^c2 * … *pk^ck
约数个数： (c1 + 1) * (c2 + 1) * … * (ck + 1)
约数之和： (p1^0 + p1^1 + … + p1^c1) * … * (pk^0 + pk^1 + … + pk^ck)

求组合数的四种方法

卡特兰数

基础课题 889. 满足条件的01序列

题意
- 给定 n 个 0 和 n 个 1，它们将按照某种顺序排成长度为 2n 的序列，求它们能排列成的所有序列中，能够满足任意前缀序列中 0 的个数都不少于 1 的个数的序列有多少个。

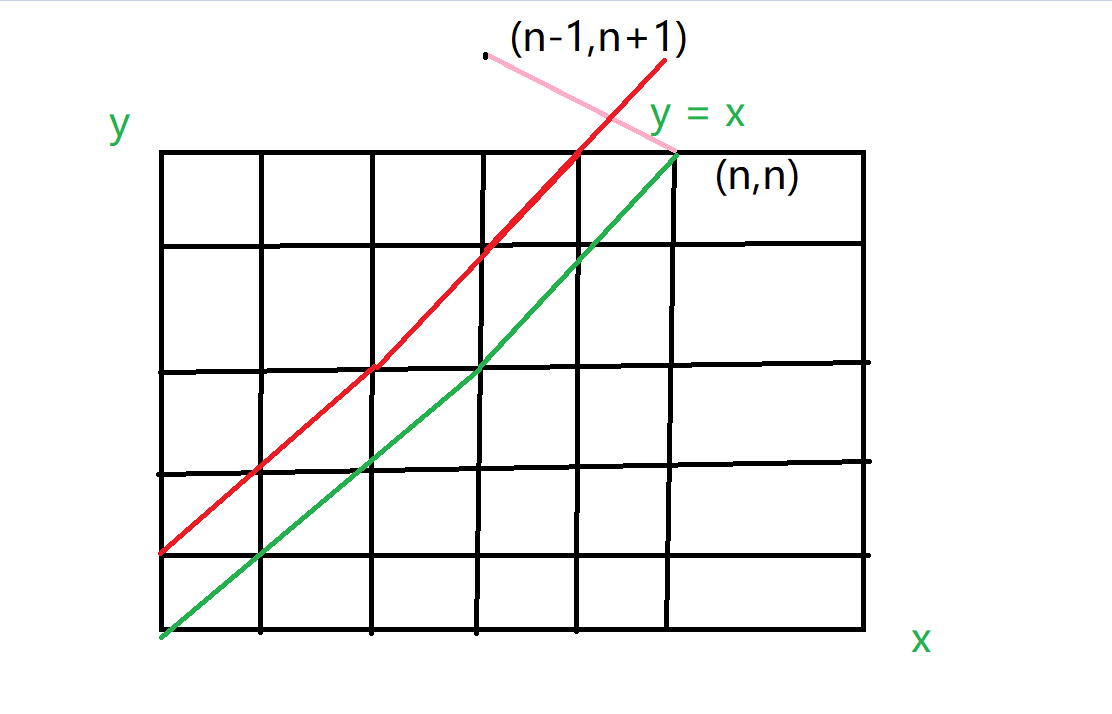
由于任意前缀种0的个数都不小于1的个数
所有可以将构造序列看做在上图中从原点走到(n,n)点，向左走代表往序列末尾加一个0，向右走代表加一个1，那么满足题意的序列就是在绿线y = x 下面，没有经过过红线及红线以上，当一个经过了红线，可以将后面的路径关于红线对称，那么终点就是（n，n）关于红线的对称点(n-1,n+1) ,所以答案其实就是求得c(2n,n) - c(2n,n-1) ;
参考代码

#include <algorithm>
#include <cstring>
#include <cstdio>
#include <iostream>

using namespace std;

typedef long long ll ;

const int mod = 1e9 + 7 ;

ll qmi(ll a,ll n){    //快速幂
    ll res = 1; 
    while(n){
        if(n & 1) res = res * a % mod ;
        a = a * a % mod ;
        n >>= 1 ;
    }
    return res ;
}

int main(){
    int n ;
    cin >> n ;

    ll res = 1 ;
    for(int i = 2 * n ; i > n ; i --) res = res * i % mod ;  //根据定义乘组合数分子的数
    for(int i = 1 ; i <= n + 1 ; i ++) res = res * qmi(i,mod - 2) % mod ;  //由于mod是素数，所有根据定义求组合数分母上的逆元

    cout << res << endl ; 
    return 0;
}

参考 ： y总提高课第五章
y总分享 常用数学知识