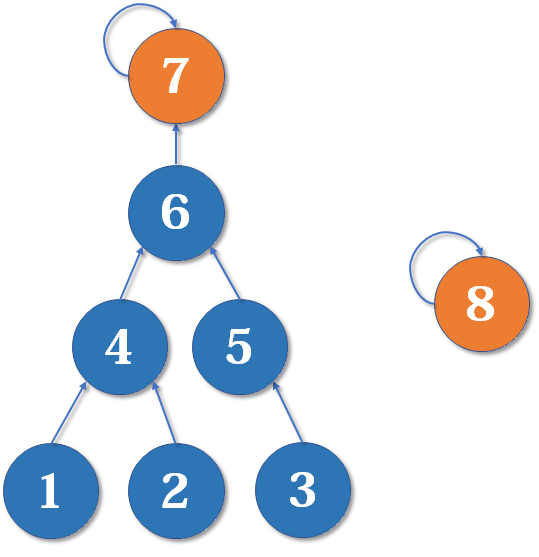
基础并查集

支持快速操作:

1. 将两个集合合并
2. 询问两个元素是否在一个集合中

并查集以树的形式维护集合, 每一个集合的编号就是根结点的编号, 每个结点都存储它的父结点
p[x] 表示 x 的父节点

1. 判断树根
   if( p[x] == x )
2. 如何求x的集合编号
   while( p[x] != x ) x = p[x]; //沿着父节点向上走
3. 如何合并两个集合x, y ( y成为x的父结点 / 集合x成为y的子集&子树 )
   p[x] = y;
4. 遍历连通块
   一般需要通过祖宗结点遍历
   p[x] == x

int p[N]; // 存储每个元素的父节点 p[x] = x

// 返回祖宗结点+路径压缩
// 返回x所在集合的编号( 即根节点的编号 )
int find( int x ) {
    if ( p[x] != x ) p[x] = find( p[x] );
    return p[x];
}
/* 优化->路径压缩：
找到x的根结点后直接让路径上的所有点都指向根节点 -> O(1) 
*/

// 初始化，假定结点编号是 1 ~ n
 for (int i = 1; i <= n; i ++ ) p[i] = i;

// 合并a和b所在的两个集合：
  p[find(a)] = find(b);

维护集合大小size[ ]的并查集

    int p[N], size[N];
    //p[]存储每个点的祖宗节点, size[]只有祖宗节点的有意义，表示祖宗节点所在集合中的点的数量

    // 返回x的祖宗节点
    int find(int x) {
        if (p[x] != x) p[x] = find(p[x]);
        return p[x];
    }

    // 初始化，假定节点编号是1~n
    for (int i = 1; i <= n; i ++ )
    {
        p[i] = i;
        size[i] = 1; // 最开始每个集合只有一个点
    }

    // 合并a和b所在的两个集合：
    size[find(b)] += size[find(a)]; // 注意合并前要先计算size
    p[find(a)] = find(b);

维护到根节点距离的并查集：

    int p[N], d[N];
    //p[]存储每个点的祖宗节点, d[x]存储x到p[x]的距离

    // 返回x的祖宗节点
    int find(int x)
    {
        if (p[x] != x)
        {
            // 记录根节点
            int u = find(p[x]);
            // 该节点到根节点距离 = 到父节点距离 + 父节点到根节点距离
            d[x] += d[p[x]];
            // 路径压缩
            p[x] = u;
        }
        return p[x];
    }

    // 初始化，假定节点编号是1~n
    for (int i = 1; i <= n; i ++ )
    {
        p[i] = i;
        d[i] = 0;
    }

    // 合并a和b所在的两个集合：
    p[find(a)] = find(b);
    d[find(a)] = distance; // 根据具体问题，初始化find(a)的偏移量