树状数组的由来

因为数组修改一个数的时间复杂度是O(1)，算一个区间的和的时间复杂度是O(n)

而前缀和修改一个数的时间复杂度是O(n)，算一个区间的和的时间复杂度是O(1)

现在我们想找一个不论怎么做都是$O(log_2n)$的，这个就是树状数组

其实，如果你乐意，你可以叫他二进制分组区间和

树状数组的定义

一般的树状数组，我们一般用$tr[N]$来表示

$tr[x]$的定义如下

我们现在设$x=(.....1000…)_2$，并且设有1的那一位为从左往右数第k+1个数，之前所有都是0

则$tr[x]$内部存的是$a[x-2{k}+1]+a[x-2{k}+2]+…+a[x]$​

由此，我们可以画出如下图片来表示各个$tr[i]$覆盖的长度（其中的C是这里的tr）

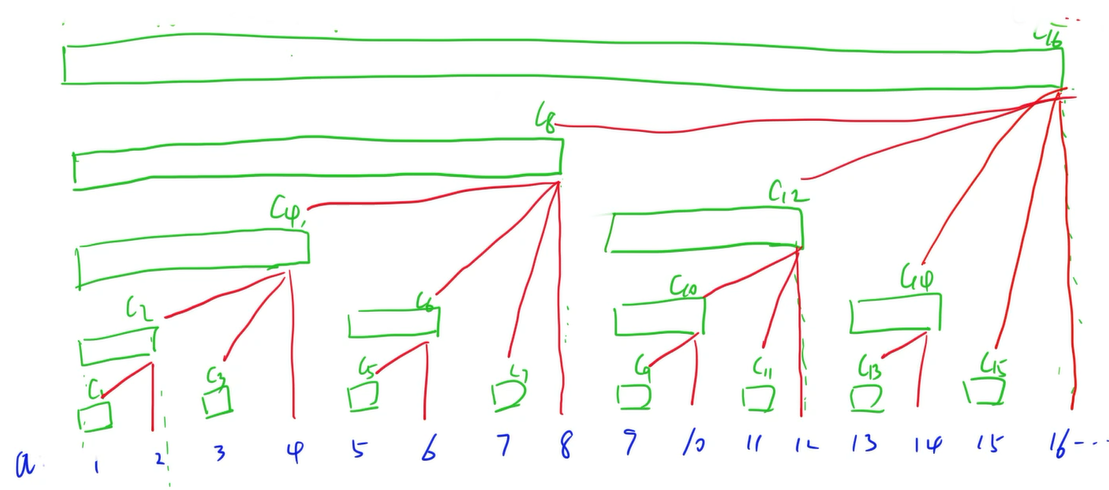
由此我们可以看出，最终的计算关系像一棵树，那些覆盖长的tr[i]就由覆盖端的tr[i]和a[i]算出来

由此我们可以定义，这些构成长的树状数组的结点为长树状数组的子结点，比如tr[7]就是tr[8]的子节点；而反之，tr[8]就是tr[7]的父节点。又因为由二进制的性质，每个长的最优表示（既花费最少的短的）都是唯一的。所以每个父节点都有那么几个固定的子节点，而每个子节点，一个固定的父节点。嗯，这个性质就很像树了，所以我们称之为树状数组嘛。

列举子节点

因为二进制的一些性质

比如$(10100000,10110000]$（这个是tr[176]的覆盖区间）,就可以被分成$(10101111,10110000]$+（这个代表的是a[176]，由上图我们不难看出，每个结点的子节点必然包括本身的a）$(10101110,10101111]$+（tr[175]，可以认为是代表tr[176-1]）$(10101100,10101110]$+$(10101000,10101100]$+$(10100000,10101000])$

由此可以看出，对于tr[x]前面有多少个0，就可以被分成多少个+1个子区间，而这些区间又构成了tr[x]

所以，列举子节点的代码如下

void find_s(int p) //列举出p的全部构成
{
    cout << "a[" << p << "] "; //因为tr[x]必定要加a[x]
    for (int i = p - 1; lowbit(i) < lowbit(p) && i > 0; i -= lowbit(i))
        cout << "tr[" << i << "] ";
    return;
}

寻找父节点

既在上面的前提下逆向寻找自己会构成谁。因为上面是把最低位分解了，这里只要加上分解的那一点就还原了，既

int find_p(int x) //找到x的父节点
{
    return x + lowbit(x);
}

初始化树状数组

这里其实有两种思路，一种是算完以后主动加上去（既自己找父节点），一种是每次加都要列举一次（既自己找子节点）

找父节点的代码的思路如下

void init_by_p() //从自己加上去的初始化算法
{
    for (int i = 1; i <= n; ++i)
    {
        tr[i] += a[i];         //因为前面的子节点都自己加上来了，直接加上自己就是完整的了
        int p = i + lowbit(i); //然后找到自己的父节点
        if (p <= n)            //如果父节点还没出界
            tr[p] += tr[i];    //那就加上去
    }
    return;
}

找子节点的代码思路如下

void init_by_s() //找到后再加上去
{
    for (int i = 1; i <= n; ++i)
    {
        tr[i] = a[i]; //我至少有自己
        for (int j = i - 1; j > 0 && lowbit(j) < lowbit(i); j -= lowbit(j))//穷举所有的子节点
            tr[i] += tr[j];
    }
    return;
}

求前缀和

因为区间是按照最小为1位分的，1~x中的x抽丝剥茧即可

比如我们求的是$(0,11101110]$，我们就可以根据树状数组的性质找到$(0,10000000]$+$(10000000,11000000]$+$(11000000,11100000]$+$(11100000,11101000]$+$(11101000,11101100]$+$(11101100,11101110]$即可

完整代码如下

int sum(int x) //求前缀和
{
    int sum = 0;
    for (int i = x; i > 0; i -= lowbit(i))
        sum += tr[i];
    return sum;
}

修改数组以后树状数组的维护

a[i]修改后会产生一个增量x，而这个增量也就是tr[i]的增量，tr[i]进行了增量变化，i的父节点也会面对增量变化，以此类推，直到边界

完整代码如下

void change(int i, int x) //把a[i]修改为x
{
    int k = x - a[i]; //增量
    a[i] = x;
    for (int j = i; j <= n; j += lowbit(j)) //我先修改我自己
        //然后再找到受我直接影响的父节点进行修改，然后父节点再处理他的父节点，直到边界
        tr[j] += k;                         //都要加上这个增量
    return;
}

后话

y总的算法提高课的树状数组的全部内容就这些啦，反正相当于是继单位数组和直接前缀和之后的新的求区间和的工具吧，主要用于修改和查询都比较频繁的情况

有疏漏还望指出哈

更加精细的解析可以戳这里