1 题目描述

给定一个字符串S和模板串P，所有字符串中只包含大小写英文字母以及阿拉伯数字。模板串P在字符串S中多次作为子串出现，求出模板串P在字符串S所有出现位置的起始下标。

2 朴素做法

两次for循环

for (int i = 1; i <= n; i ++) {
    bool flag = true;
    for (int j = 1; j <= m; j ++) {
        if (s[i + j - 1] != p[j]) {
            flag = false;
            break;
        }
    }
    if (flag) {
        // i这个点就是匹配的起始点
    }
}

3 优化

约定：字符串下标从1开始。

首先介绍字符串前缀和后缀的定义：

对于字符串A和B，存在A=BS，其中S是任意字符串，那么B就是A的前缀。同理可以定理后缀。

• 比如 abc的前缀包括{a, ab}，后缀包括{bc, c}

根据字符串前缀和后缀可以构建一个 next 表，其中值表示字符串前缀集合与后缀集合的交集中元素长度的最大值。

• 例如，对于aba，它的前缀集合{a, ab}；后缀集合{ba, a}，它在next 表中的值为1

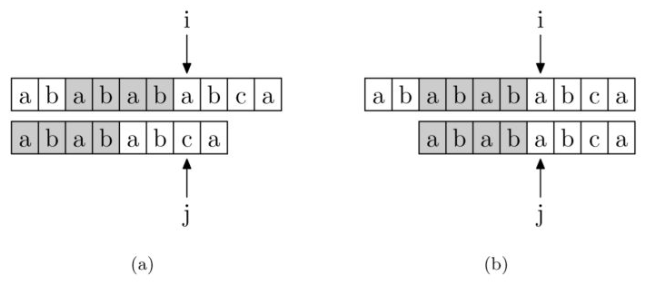
如果要在主字符串 ababababca 中查找模式字符串 abababca。如果在 j 处字符不匹配，那么由模式字符串PMT的性质，主字符串中 i 指针之前的PMT[j-1] 位就一定与模式字符串的第 1位至第 PMT[j-1] 位是相同的。因为主字符串在 i 位失配，也就意味着主字符串从 i-j+1 到 i-1 这一段与模式字符串 1 到 j-1 这一段是完全相同的。

以图中例子来说，在 i 处失配，那么主字符串和模式字符串的前6位就是相同的。又因为模式字符串的前 6 位的前 4 位后缀和前缀是相同的，所以可以推出主字符串 i 之前的 4 位和模式字符串开头的 4 位是相同的，就是图中灰色部分，那么这部分就不用再比较了。

实现：

#include <bits/stdc++.h>
using namespace std;

const int N = 100010, M = 1000010;
int n, m;
char s[M], p[N];
int ne[N];

int main()
{
    cin >> n >> p + 1 >> m >> s + 1;

    // 求 next 数组 p[i] 和 p[j + 1]匹配
    for (int i = 2, j = 0; i <= n; i ++) {
        while(j && p[i] != p[j + 1]) j = ne[j];
        if (p[i] == p[j + 1]) j ++;
        ne[i] = j;
    }

    // kmp 过程 s[i] 和 p[j + 1] 匹配
    for (int i = 1, j = 0; i <= m; i ++) {
        while(j && s[i] != p[j + 1]) j = ne[j];
        if (s[i] == p[j + 1]) j ++;
        if (j == n) {
            printf("%d ", i - n);
            j = ne[j];  // 继续下一个点
        }
    }
}