What is 线索二叉数(TBT)
线索二叉树是一种优化的二叉树结构,对于以结构体指针实现二叉树的方案进行了顺序遍历的优化
但是。随着计算机内存的加大,他所能带来的优势反而十分局限
- 线索二叉树对二叉树的改进
- 线索二叉树的实现思路
- 线索二叉树的实例
1,线索二叉树对二叉树的改进
二叉树我们很熟哇,对于一个用结构体指针完成的二叉树结构,我们可以可以看到
实际上,我们定义了大量没得意义的指针,这些指针为空
面对数据范围巨大的要求,过多指针的浪费是非常危险的,但是这种情况是结构体指针方案所难以避免的,而我们使用结构体指针其实也是难以避免的
而当我们对二叉树进行不从根结点开始的顺序遍历时,我们要想找到该节点的前趋和后继的结点,我们又必须从根开始遍历一遍<_<
要想不反复遍历,我们就有两个解决方案,一个是重新建一个数组,先遍历一遍,然后记下来;
还有一种,则是我们的线索二叉树解决方案了,这种方案相较上面的方案,不需要重新建数组,直接利用二叉树浪费的空指针完成遍历的记录
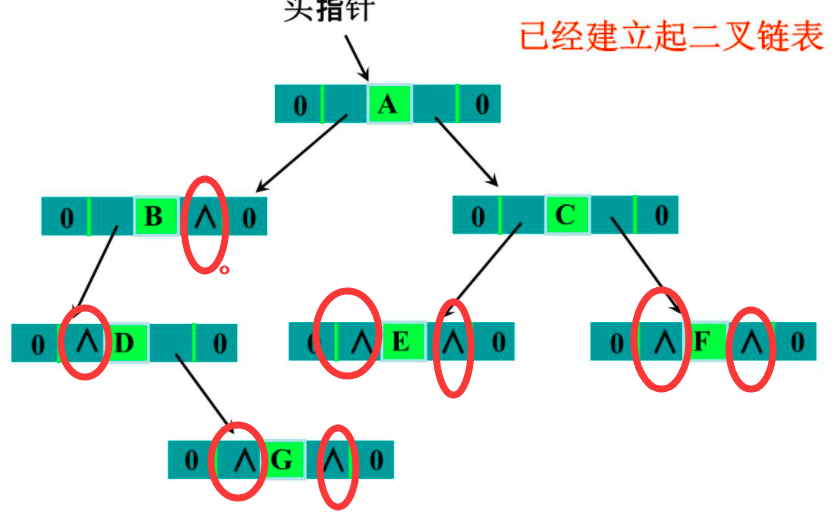
就比如说上面那个二叉树,如果我们要求对于它中序遍历的前驱和后继我们可以这样:
注意:图中我们用原来左儿子结点指针指前驱,用原来右儿子指针指后继
由此,我们得到了一个线索二叉树!!
这个时候,举几个例子感受一下
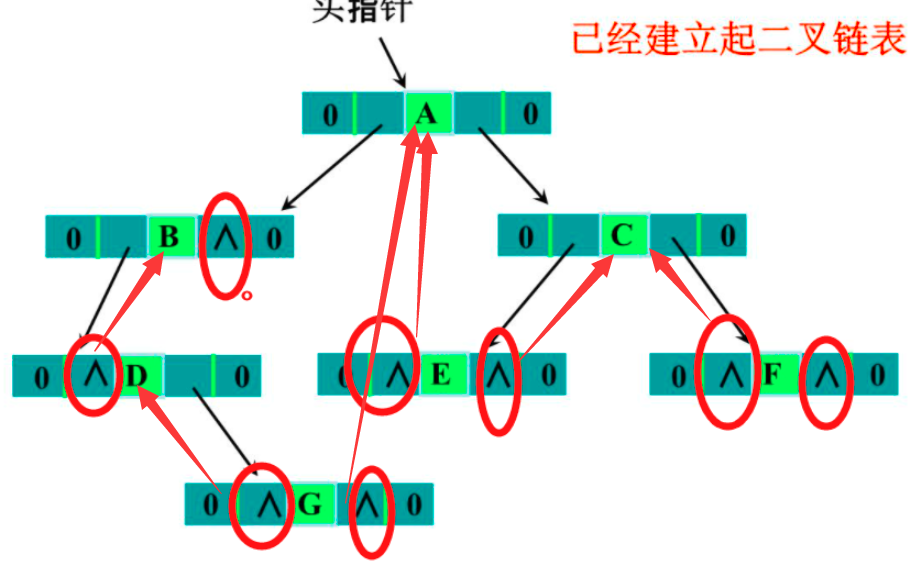
1,我要求找B的中序遍历前驱:
那我们知道,中序遍历:左根右,所以找中序遍历左子树找到(不需要搜索整树)
2,我们要求E的中序遍历后继:
直接顺着右子树,过去就是。
但是!此时我们左右子树都不是空指针,那我们怎么判断呢?
我们只好哭哭再加一个bool的一位数据来记录指向的是前驱后继还是儿子
但是,我们总可以认为,拿一个1位的bool换一个4位的指针不亏吧。。。
吧。。。(但是每个结点都要有。。不过我们还是可以证明,他确实省了空间)
于是,我们遍历,然后记录,便可以很轻便的解决这个遍历速度的问题
当然了,对于较小的数据范围或者一台合格的电脑,我们很明显不需要如此去为空间操劳,但是如果我们面临着巨大的数据范围或者是在单片机上快速查询的要求,我们可以考虑这个方案
其实,我们并不会经常用到它,但是我们需要理解其内部的利用空余空间的思想
当我们有冗余的空间时,我们还得准备好之后卡农需要的东西
如果你在有钱的时候买了保险,那么你将会在需要的时候不那么绝望
如果我们需要存储前序和后序也是可以的!参考中序排列时的做法
2,线索二叉树实现思路
先遍历一遍:
在遍历的上一步,记下指针
在遍历的这一步,如果记下前驱的指针空着,就指到上面那一个
如果后继指针空着,记下来(记一个指向指针的指针)
在遍历的下一步,把自己的指针传给前一个结点的后继指针
就是介样
模板以后补上
3. 线索二叉树的实例
以后补上TAT
收藏啦!以后会更新的!

