图的最短路算法 All in one
预备知识:
图的相关概念,图的邻接矩阵储存形式
对于一般的不带权值的图,我们一般用BFS就可以很轻松的得到最短路,但是对于带权的图,我们必须需学会一些有用的最短路算法>_<
接下来我们将会介绍Floyed多源最短路算法,Dijkstra单源最短路算法,Ford单源最短路算法和Ford升级版SPFA算法,并具体阐述他们的实现思路,应用场景,复杂度和模板代码
- Floyed多源最短路算法
- Dijstra单源最短路算法
- Foed单源最短路算法
- SPFA:升级版Ford
Floyed多源最短路 O(N^3)
这个算法相当暴力,并且复杂度也不算友好,但是其思路十分简单:枚举
怎么枚举呢,相信你一看代码就明白了:(来自:yxc闫总 )
//INF是初始化值,有边则表示边权,没有边则表示无限
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= n; j ++ )
if (i == j) d[i][j] = 0;
else dis[i][j] = INF;
// 算法结束后,dis[a][b]表示a到b的最短距离
void floyd()
{
for (int k = 1; k <= n; k ++ )
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= n; j ++ )
dis[i][j] = min(dis[i][j], dis[i][k] + dis[k][j]);
}
算法思路流程:
1,首先,把点1,j之间的最短路初始化为i,j之间的边权(无边则无限,自环则为0)
2,然后,开始Floyed暴力枚举:
(1)先枚举每一个点,作为中间点
(2)再继续无脑枚举每一个点,作为起始点
(3)然后再继续无脑枚举每一个点,作为结束点
(4)**如果起始点到中间点的最短路+中间点到结束点的最短路<直接算起始点到结束点的最短路,那么就把起始点到结束点的最短路刷新**
3,然后,完事收工,**O(N^3)**
非常的简单非常的暴力,但是却可以得到相当好的多源最短路的效果
不过这个流程并不方便用剪枝,所以一般只可以对付数据量较小或者有必要求多源最短路的时候
当然了,Floyed算法还可以解决图的连通性为问题
正确性证明:
设从i到j的最短路径为m(i,a1,a2,a3,……an,j)
在Floyed算法中,必有任意ak被枚举
对于被枚举的任意ak,必有数列m中任意两数被枚举
若有i,j的最短路,m(i,a1,a2,a3,……an,j)
对于每一个可能的结果,只保留最优结果,而所有结果无漏解
就是酱紫平凡的Floyed^_^
Dijkstra单源最短路算法 O(N^2)
相较于Floyed算法来说,Dijstra算法更为灵活,但是复杂度并没有好转,如果想要用Dijstra算法写多源最短路的话,也要O(N^3)的复杂度,但是对于只对一点的最短路有需求的情况却非常合适,朴素的Dijstra算法并不能正常处理负边权的情况,但是,我们可以很灵活的对Dijsra算法进行改造。
Dijstra算法利用了枚举和贪心的思想,先上流程:
设:dis[i]表示从点1到点i的最短路
0,初始化dis[i],如果1,i之间有边,dis[i]=w[1][i];否则,等于无限(极大数)
{
**1,枚举所有没有被访问过的点i,使dis[i]最小
2,标记dis[i]已经被访问,并且已经满足最短路
3,枚举每一个和i相连接的未访问的点v(更新路径):**
dis[v]=min(dis[v],dis[i]+w[i][v]);
}
以上步骤循环n-1遍,直到所有点都被标记访问
看不懂文字的,几张图就明白了:
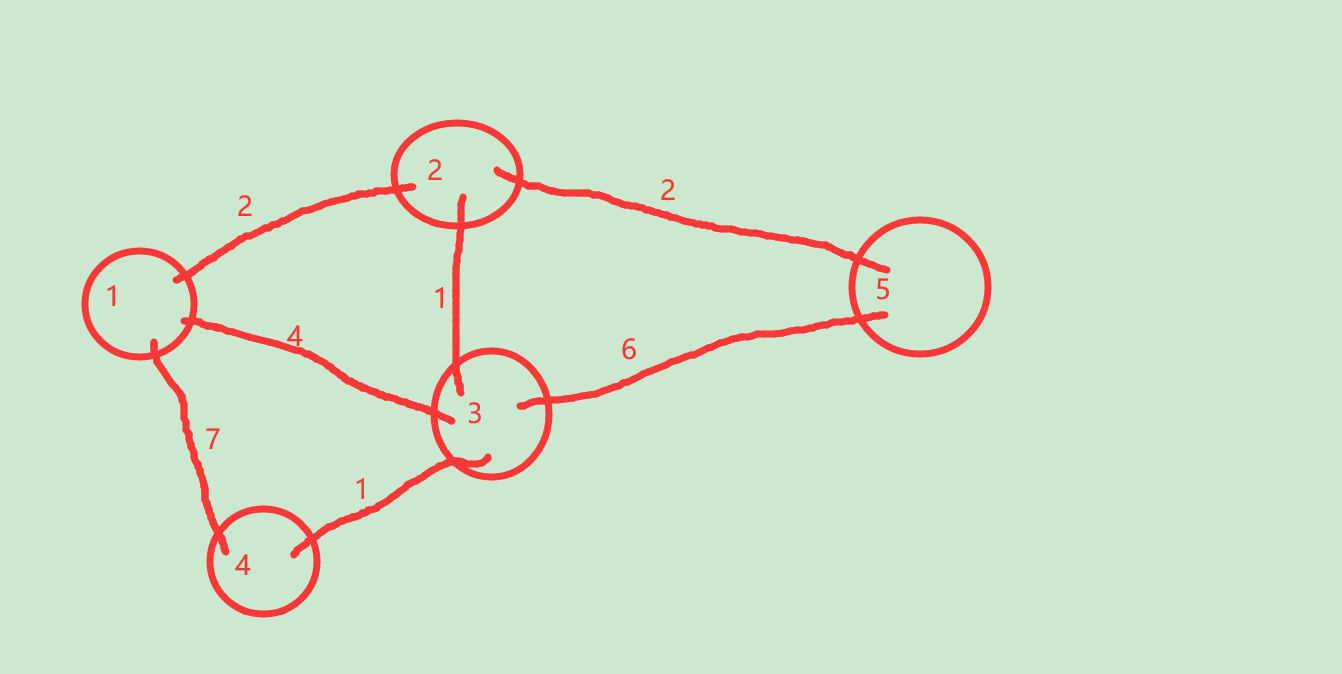
1,
此时,初始化为:
dis[2]=2,dis[3]=4,dis[4]=7,dis[5]=无限
找到dis[2]最小,为2,于是标记2已经找到最短路
然后枚举和2相连的3,5,更新dis[3]=3,dis[5]=4
2,
此时,得
dis[2]=2,dis[3]=3,dis[4]=7,dis[5]=4
找到dis[3]最小,为3(2已经访问过了),于是标记3已经找到最短路径
然后枚举和3相连的4,5,更新dis[4]=4
3,
此时,得
dis[2]=2,dis[3]=3,dis[4]=4,dis[5]=4
找到dis[4]最小,标记
更新5(然而并没有成功)
4,
dis[2]=2,dis[3]=3,dis[4]=4,dis[5]=4
找到dis[5],标记
完毕
可以看到,Dijstra算法可以非常有效的找出单元最短路,尽管看上去复杂度为O(N^2)但是,到后期大部分节点都标记之后就会非常高效,所以实际执行次数会小于N^2
重点来了,Dijstra算法正确性证明:
关键在于:为什么Dijstra算法可以直接标记当前最小dis[i]为已知最短路?
设有最短路dis[j]+w[i][j]为更短路,但是dis[i]一定小于dis[j],若w[i][j]不为负数,则dis[i]<=dis[j]+w[i][j]
现在知道为啥不能处理负边权了吧!!
所以,dis[i]没有更短路径,可以标记出炉
就是酱紫,接下来上模板啦!(来自:yxc闫总 )
int w[N][N]; // 存储每条边
int dis[N]; // 存储1号点到每个点的最短距离
bool st[N]; // 存储每个点的最短路是否已经确定
// 求1号点到n号点的最短路
void dijkstra()
{
get(dis); //初始化dis
dis[1] = 0;
for (int i = 0; i < n - 1; i ++ )
{
int t = -1; // 在还未确定最短路的点中,寻找距离最小的点
for (int j = 1; j <= n; j ++ )
if (!st[j] && (t == -1 || dist[t] > dist[j]))
t = j;
// 用t更新其他点的距离
for (int j = 1; j <= n; j ++ )
dis[j] = min(dis[j], dis[t] + w[t][j]);
st[t] = true;
}
}
模板的结构也是非常清晰好懂滴!我就不赘述了
其实,我们还可以对Dijstra算法进行一个小优化,既然我们需要不断地寻找最小的dis值那么我们当然可以建立一个小根堆,这样我们查找最小dis值的过程就会快得多啦!
下面的模板使用了STL库里面的优先队列(priority)_queue)和元组(pair)
typedef pair<int,int> PII;
void dijkstra()
{
get(dis);
dist[1] = 0;
priority_queue<PII, vector<PII>, greater<PII>> heap;
heap.push({0, 1}); // first存储距离,second存储节点编号
while (heap.size())
{
auto t = heap.top();
heap.pop();
int ver = t.second, distance = t.first;
if (st[ver]) continue;
st[ver] = true;
for (int i = h[ver]; i != -1; i = ne[i])
{
int j = e[i];
if (dist[j] > distance + w[i])
{
dist[j] = distance + w[i];
heap.push({dist[j], j});
//只用加入,因为比原来的小,只找n-1个轮不到原来那个,而上面有特判
}
}
}
}
Dijstra也是非常滴友好呢!^_^
Ford单元最短路算法 O(NE) (N:顶点数,E:边数)
一看复杂度就知道,O(NE),点数*边数,这说明Ford在稀疏图中的效率将会吊打Dijstra,但是在稠密图中又会比Dijstra慢很多
Ford算法可以解决存在负边权的问题,但是无法解决存在负权回路的问题
不过,Ford的思想也非常简单,而且和冒泡排序的思想有那么一点的神似
Ford算法的流程思路是这样的:
1,初始化:dis[1]=0;其他都是无限(超大),并且认为dis[1]为已知最短路径,其他都未确定
{
2,枚举每一条边,获取这条边连接的两点i,j和该边的边权w:
dis[i]=min(dis[j]+w,dis[i]);
dis[j]=min(dis[i]+w,dis[j]);
}
以上操作循环N次
其实很好理解,就是不断枚举每一个边,并且每次不断通过修改值(不断缩小)达到最优
而冒泡算法,也是不断枚举每两个相邻的元素,通过不断交换达到有序
而对于Frod和冒泡来说,重复n次操作并不是有什么具体意义,而是解决最坏情况所需要的次数
Ford正确性证明:
**
设dis[i]的最短路径为:(1,a,b,c,……i)(注意:a,b,c……是边)
我们知道,中途最多经过n个点,对于n个点,有n-1条边
我们对于每条边所对应的的两点,我们分别枚举了n次:
即我们考虑了所有的情况,并且只保留了最优值**
嗯,思路依旧十分的友好,接下来我们直接上模板!!(来自:yxc闫总 )
这是有向图的,无向图的可以简单类推
int n, m; // n表示点数,m表示边数
int dist[N]; // dist[x]存储1到x的最短路距离
struct Edge // 边,a表示出点,b表示入点,w表示边的权重
{
int a, b, w;
}edges[M];
//结构体也可以用二维数组模拟,f[i][0],f[i][1]是两点,f[i][2]是边权
// 求1到n的最短路距离,如果无法从1走到n,则返回-1。
void ford()
{
get(dis); //初始化
dis[1] = 0;
// 如果第n次迭代仍然会松弛三角不等式,就说明存在一条长度是n+1的最短路径,由抽屉原理,路径中至少存在两个相同的点,说明图中存在负权回路。
for (int i = 0; i < n; i ++ )
{
for (int j = 0; j < m; j ++ )
{
int a = edges[j].a, b = edges[j].b, w = edges[j].w;
if (dist[b] > dist[a] + w)
dist[b] = dist[a] + w;
}
}
}
Ford也非常的简单^_^
SPFA,升级版Ford O(E)!! 终于线性级的了qwq(平均情况)
SPFA可以说是融合了BFS和Ford的高效算法,除了暂时的开对列带来的空间消耗外,相比较传统的Ford的效率有大幅度提高!
说BFS是因为,改变之后写法非常像BFS,并且运用到了队列;说Frod是因为,本质上SPFA就是对Ford算法的一种剪枝优化操作!!!
为什么这么说呢,先说说Ford哪里可以剪枝:
举个例子,下面这张图:

对,这个和Dijstra那张图是一样的,我们试着用Frod的思路来推一下这张图:
1,dis[1]=0,dis[2]=2,dis[3]=4,dis[4]=7,dis[5]=无限
2,dis[1]=0,dis[2]=2,dis[3]=3,dis[4]=4,dis[5]=4
3,4,5都没有任何改变,第2步之后已经是最短路了-_-
那么,问题就出来了:
1,在一次循环的时候,我们知道dis[5]的两条边连向的点还没有赋值,但是还是枚举了这个边,实际上在第一轮里有用到的只有和1节点相连的边
2,在大部分的情况中,都不需要真正执行N次,只有最最最坏的情况才需要这么多,但是我们却把每种情况都当做最坏的,浪费了非常多的时间却并有使结果更优
这就是问题所在!!!SPFA正是通过解决这些问题达到剪枝的效果,从而大大提高效率!
接下来,讲讲SPFA是如何利用队列来完成Ford的剪枝的!
上流程:
//我们需要一个队列,两个指针(或者用STL模板),和一个判断该点是否在队列中的bool数组exits
//注意!exits不是判重!当一个数据出队后又会恢复false,它只是用来存储队列当前有哪些元素,只是为了避免重复存在相同元素在对列中!!
//还应该提前准备好一个数组保存所有连接i(或从i出发)的边!
//这里用E[i][n],表示和i相连的边集合,共有p[i]条
1,初始化:原有的和Ford一样,对列中只放1节点,exits[1]=true,其余为false
2,开始对列的循环
{
(1)取出队首元素i,exits[i]=false
(2)循环每一条和i相连的边
for(int m=0;m<f[i];m++){
(3)更新
if(dis[E[i][m]]>dis[i]+w[i][E[i][m]]){
dis[E[i][m]]=dis[i]+w[i][E[i][m]];
(4)加入新节点
if(!exits[E[i]][m]){
exits[E[i][m]]=true;
//入队。。。
}
}
}
Over~!
原理和证明也和Frod一样,只是在Frod的基础上完成了剪枝!!
上模板:
//懒得改了,毕竟很清晰
int n; // 总点数
int h[N], w[N], e[N], ne[N], idx; // 邻接表存储所有边
int dist[N]; // 存储每个点到1号点的最短距离
bool st[N]; // 存储每个点是否在队列中
// 求1号点到n号点的最短路距离,如果从1号点无法走到n号点则返回-1
void spfa()
{
get(dist)
dist[1] = 0;
queue<int> q;
q.push(1);
st[1] = true;
while (q.size())
{
auto t = q.front();
q.pop();
st[t] = false;
for (int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];
if (dist[j] > dist[t] + w[i])
{
dist[j] = dist[t] + w[i];
if (!st[j]) // 如果队列中已存在j,则不需要将j重复插入
{
q.push(j);
st[j] = true;
}
}
}
}
}
SPFA Over~~
P.S.其实最短路是图论里头最简单的东西之一了QAQ

