例题1142. 繁忙的都市

二分 + 并查集

c++代码

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 310,M = 8010;
int pa[N];
struct Edge{  
    int a,b,w;
    //构造函数
    Edge(){}   
    Edge(int a,int b,int w):a(a),b(b),w(w){}
    bool operator <(const Edge& W) const{
        return w < W.w;
    }
}edges[M];
int n,m;


int find(int x){   //将连通块所有节点指向祖宗节点并返回
    if(pa[x] != x) pa[x] = find(pa[x]);
    return pa[x];
}



bool check(int maxC)    //利用并查集判断联通块是否含有n个点
{
    for(int i = 0; i < N; i ++) pa[i] = i;

    for(int i = 0; i < m; i ++)  //合并
    {
        int a = edges[i].a, b = edges[i].b, w = edges[i].w;
        if(w > maxC) break;  //一直枚举到有边的权值大于maxc为止
        a = find(a), b = find(b);
        if(a != b) pa[a] = b;
    }

    int pp = find(pa[1]);
    for(int i = 2; i <= n; i ++)
        if(find(i) != pp)
            return false;
    return true;
}


int main(){
    cin >> n >> m;

    for(int i = 1;i <= n;++i){   //初始所有节点的祖宗节点都是自己
        pa[i] = i;
    }

    for(int i = 0;i < m;++i){
        int a,b,w;
        cin >> a >> b >> w;
        edges[i].a = a , edges[i].b = b , edges[i].w = w;
    }

    sort(edges,edges + m);  //排序，进行二分


    int l = 1,r = 10010,mid = 0;
    while(l < r){
        mid = l + r >> 1;
        if(check(mid)) r = mid;
        else l = mid + 1;
    }
    cout << n - 1 << ' ' << r << endl;
    return 0;
}

例题： 5845. 你能穿过矩阵的最后一天

反向求解 + 超级源点 + 并查集判连通性

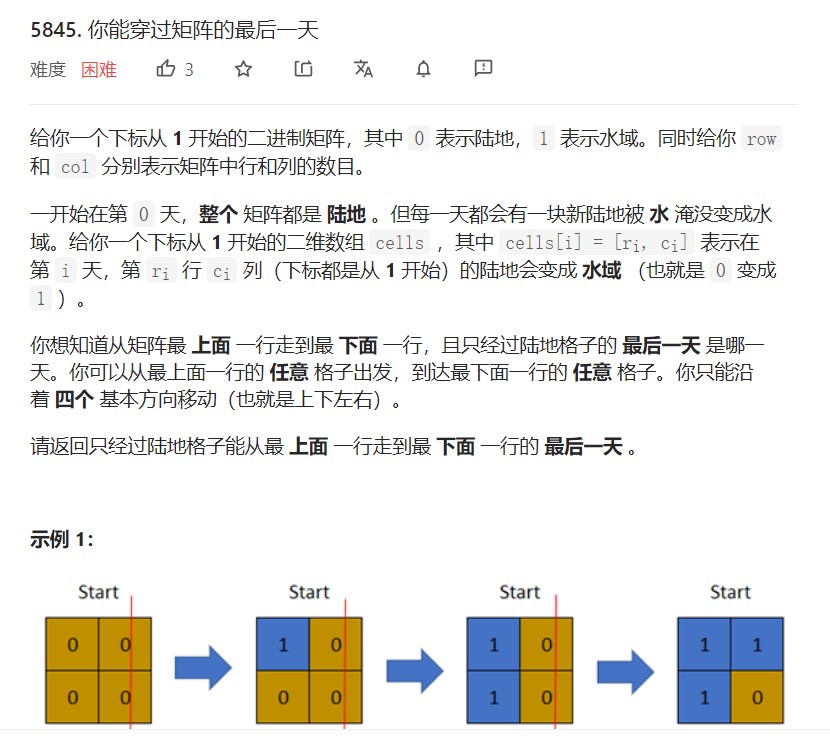
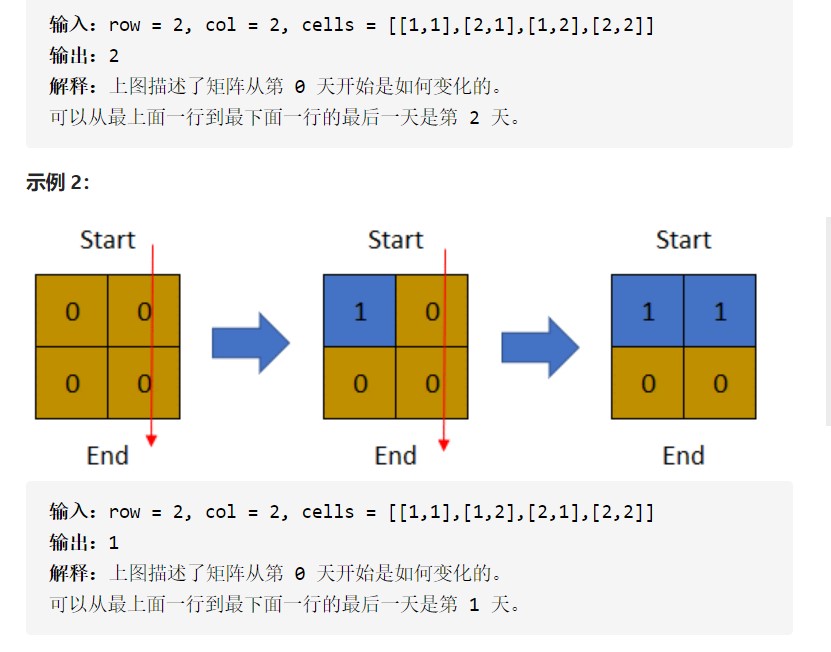
思路

• 有多个起点和终点，所以创建两个超级源点

• 从后面往前面推，从后面增加陆地，如果两个超级源点之间联通

• 那么说明找到了最上面一行走到最下面 一行的最后一天

/*
    有多个起点和终点，所以创建两个超级源点
    从后面往前面推，从后面增加陆地，如果两个超级源点之间联通
    那么说明找到了最上面一行走到最下面 一行的最后一天 。
*/
class Solution {
public:
    int latestDayToCross(int row, int col, vector<vector<int>>& cells) {
        int fx[4][2] = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
        //定义两个超级源点s,t,编号分别为row * col 和 row * col + 1
        vector<int> pre(row * col + 2);  //祖宗数组
        vector<vector<bool>> vis(row, vector<bool>(col, false));  //当前点是否是陆地

        for(int i = 0; i < pre.size(); i ++){    // 初始化并查集
            if(i < col)  //第一行连接源点s
                pre[i] = row * col;
            else if(i >= (row - 1) * col && i < row * col)  //最后一行与源点t相连
                pre[i] = row * col + 1;
            else
                pre[i] = i;
        }

        //恢复成陆地并构造并查集
        for(int i = cells.size() - 1; i >= 0; i --){    // 时光倒流
            int r = cells[i][0] - 1, c = cells[i][1] - 1;
            vis[r][c] = true;
            for(int i = 0; i < 4; i ++){
                int newr = r + fx[i][0];
                int newc = c + fx[i][1];
                //邻接的点合法且是陆地
                if(newr >= 0 && newr < row && newc >= 0 & newc < col && vis[newr][newc]){                   
                    int a = find(r * col + c, pre); //原状态
                    int b = find(newr * col + newc, pre);  //新状态
                    if(a != b)
                        pre[a] = b;
                }
            }
            if(find(col * row, pre) == find(col * row + 1, pre))
                return i;
        }
        return 1;
    }

    int find(int a, vector<int> &pre){
        return a == pre[a] ? a : pre[a] = find(pre[a], pre);
    }
};