超全经典排序大汇总

算法思想

首先,扫描一下整个原始序列 $a$，获取最小值 $min$ 和最大值 $max$，其次开辟一块新的存储空间 $b[ ]$,该数组长度为 $ d = max - min + 1$，$b[d]$中存储的是在min~max之间的相应数值出现的次数，如：$b[5] = 2$,表示 $5$ 出现 $2$ 次，最后根据 $b$ 数组的统计的元素次数,依次输出各元素。

inference

时间复杂度

1. 最好 — $O(n + m)$
2. 最坏 — $O(n + m)$
3. 平均 — $O(n + m)$

演示动画

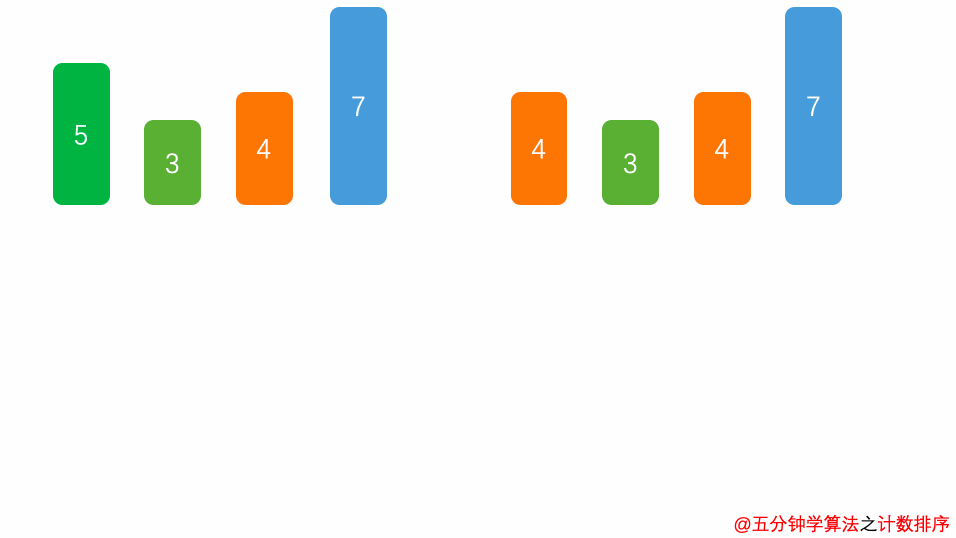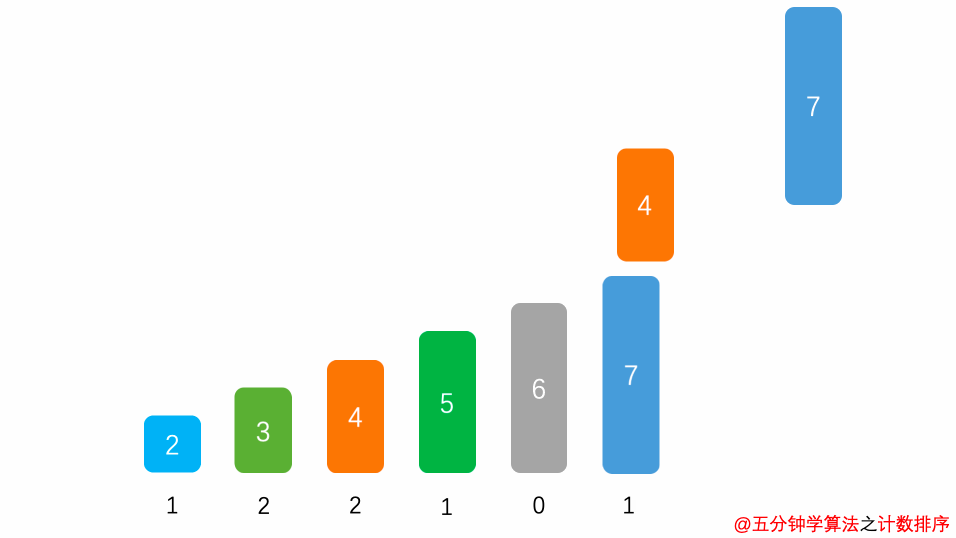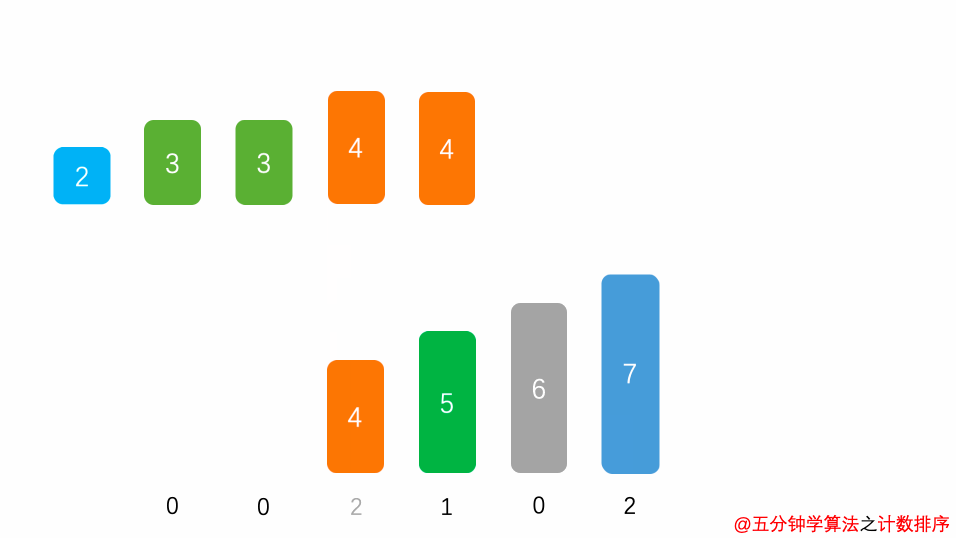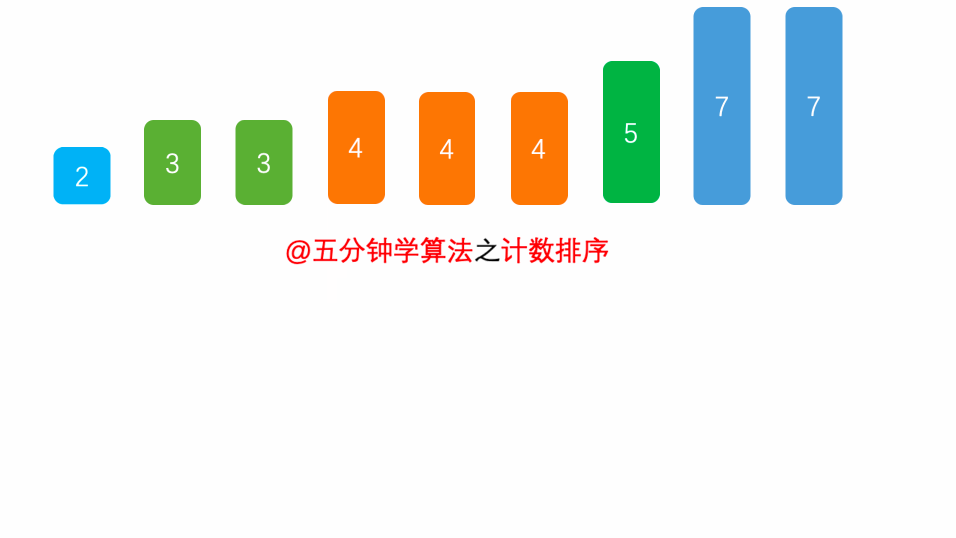
空间复杂度

稳定性

稳定、不稳定均可设定

算法特点

1.当数列最大最小值差距过大时，并不适用计数排序。

比如给定20个随机整数，范围在0到1亿之间，这时候如果使用计数排序，需要创建长度1亿的数组。不但严重浪费空间，而且时间复杂度也随之升高。

2.当数列元素不是整数，并不适用计数排序。

如果数列中的元素都是小数，比如25.213，或是0.00000001这样，则无法创建对应的统计数组。这样显然无法进行计数排序。

算法适用性

1. 顺序表
2. 链表

朴素版特点

1. 代码简洁、易实现
2. 由于根据最大值开辟存储空间,可能造成空间的浪费,因此耗费存储空间大
3. 无法保证元素的稳定性

核心代码

//朴素版 
void CountSort(int a[], int n){
    int minval = a[0], maxval = a[0];
    for(int i = 0; i < n; i ++){//遍历数组求得最大值和最小值 
        minval = min(minval, a[i]);
        maxval = max(maxval, a[i]);
    }

    int cnt[maxval + 1] = {0};//根据最大值开辟新数组空间 

    for(int i = 0; i < n; i ++) cnt[a[i]] ++;//统计原数组中元素出现的次数 

    for(int i = minval, k = 0; i <= maxval; i ++){
        while(cnt[i] != 0){
            data[k ++] = i;//将排序后的序列赋给原数组 
            cnt[i] --;//i出现的次数减1 
        }
    }
}

完整代码

#include <iostream> 
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <fstream>

using namespace std;
const int N = 200;//注意数组越界问题,开大点 

int num;
int data[N],idx;

//朴素版 
void CountSort(int a[], int n){
    int minval = a[0], maxval = a[0];
    for(int i = 0; i < n; i ++){//遍历数组求得最大值和最小值 
        minval = min(minval, a[i]);
        maxval = max(maxval, a[i]);
    }

    int cnt[maxval + 1] = {0};//根据最大值开辟新数组空间 

    for(int i = 0; i < n; i ++) cnt[a[i]] ++;//统计原数组中元素出现的次数 

    for(int i = minval, k = 0; i <= maxval; i ++){
        while(cnt[i] != 0){
            data[k ++] = i;//将排序后的序列赋给原数组 
            cnt[i] --;//i出现的次数减1 
        }
    }
}

int main(){
    //打开文件 
    ifstream infile;
    infile.open("D:\\学习\\数据结构\\第8章排序\\in.txt", ios::in);

    //写文件 
    ofstream outfile;
    outfile.open("D:\\学习\\数据结构\\第8章排序\\out.txt", ios::out);

    if(!infile.is_open()){//判断文件打开是否成功 
        cout << "file open failure!" << endl;
    }

    infile >> num;//读取元素个数 
    while(num --){//将文件中的元素复制到data[1...n] 数组中
        infile >> data[idx ++];
    }

    cout << "排序前元素序列：" << endl;
    for(int i = 0; i < idx; i ++) cout << data[i] << ' '; cout << endl;

    //cout << "使用sort函数排序后序列: " << endl;
    //sort(data, data + idx); 
    //for(int i = 0; i < idx; i ++) cout << data[i] << ' '; cout << endl;

    CountSort(data, idx);
    cout << "使用计数排序后序列为：" << endl;
    for(int i = 0; i < idx; i ++) cout << data[i] << ' '; cout << endl;

    num = idx, idx = 0, outfile << num << endl;//写入数据数num以及在行末写入\n 
    while(num --){
        outfile << data[++ idx] << ' ';//将排序后的数据写到文件中 
    }
    outfile << endl;//向文件末尾写入\n结束符 

    //关闭文件 
    infile.close();
    outfile.close();
    return 0;
}

输入数据(in.txt)

10
13 69 86 99 59 23 64 32 86 72

输出数据(out.txt)

10
13 23 32 59 64 69 72 86 86 99 

一次优化特点

1. 相比于朴素版, 空间复杂度大大降低
2. 不能保证稳定性

核心代码

//一次优化 
void CountSort(int a[], int n){
    int minval = a[0], maxval = a[0];
    for(int i = 0; i < n; i ++){//遍历数组求得最大值和最小值 
        minval = min(minval, a[i]);
        maxval = max(maxval, a[i]);
    }

    int d = maxval - minval + 1;// 计数数组的实际长度 
    int cnt[d] = {0};//根据最大值开辟新数组空间 

    //统计原数组中元素出现的次数
    for(int i = 0; i < n; i ++) cnt[a[i] - minval] ++;//将元素映射到a[0...d-1] 

    for(int i = 0, k = 0; i <= maxval - minval; i ++){
        while(cnt[i] != 0){
            data[k ++] = i + minval;//将排序后的序列赋给原数组 
            cnt[i] --;//i出现的次数减1 
        }
    }
}

完整代码

#include <iostream> 
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <fstream>

using namespace std;
const int N = 200;//注意数组越界问题,开大点 

int num;
int data[N],idx;

//一次优化 
void CountSort(int a[], int n){
    int minval = a[0], maxval = a[0];
    for(int i = 0; i < n; i ++){//遍历数组求得最大值和最小值 
        minval = min(minval, a[i]);
        maxval = max(maxval, a[i]);
    }

    int d = maxval - minval + 1;// 计数数组的实际长度 
    int cnt[d] = {0};//根据最大值开辟新数组空间 

    //统计原数组中元素出现的次数
    for(int i = 0; i < n; i ++) cnt[a[i] - minval] ++;//将元素映射到a[0...d-1] 

    for(int i = 0, k = 0; i <= maxval - minval; i ++){
        while(cnt[i] != 0){
            data[k ++] = i + minval;//将排序后的序列赋给原数组 
            cnt[i] --;//i出现的次数减1 
        }
    }
}

int main(){
    //打开文件 
    ifstream infile;
    infile.open("D:\\学习\\数据结构\\第8章排序\\in.txt", ios::in);

    //写文件 
    ofstream outfile;
    outfile.open("D:\\学习\\数据结构\\第8章排序\\out.txt", ios::out);

    if(!infile.is_open()){//判断文件打开是否成功 
        cout << "file open failure!" << endl;
    }

    infile >> num;//读取元素个数 
    while(num --){//将文件中的元素复制到data[1...n] 数组中
        infile >> data[idx ++];
    }

    cout << "排序前元素序列：" << endl;
    for(int i = 0; i < idx; i ++) cout << data[i] << ' '; cout << endl;

    //cout << "使用sort函数排序后序列: " << endl;
    //sort(data, data + idx); 
    //for(int i = 0; i < idx; i ++) cout << data[i] << ' '; cout << endl;

    CountSort(data, idx);
    cout << "使用计数排序后序列为：" << endl;
    for(int i = 0; i < idx; i ++) cout << data[i] << ' '; cout << endl;

    num = idx, idx = 0, outfile << num << endl;//写入数据数num以及在行末写入\n 
    while(num --){
        outfile << data[++ idx] << ' ';//将排序后的数据写到文件中 
    }
    outfile << endl;//向文件末尾写入\n结束符 

    //关闭文件 
    infile.close();
    outfile.close();
    return 0;
}

输入数据(in.txt)

10
13 69 86 99 59 23 64 32 86 72

输出数据(out.txt)

10
13 23 32 59 64 69 72 86 86 99 

二次优化特点

1. 相比于朴素版, 空间复杂度大大降低
2. 可以保证稳定性，该排序稳定

核心代码

//二次优化 
void CountSort(int a[], int n){
    //遍历数组求得最大值和最小值
    int minval = a[0], maxval = a[0];
    for(int i = 0; i < n; i ++){ 
        minval = min(minval, a[i]);
        maxval = max(maxval, a[i]);
    }

    int d = maxval - minval + 1;// 计数数组的实际长度 
    int cnt[d] = {0};//根据最大值开辟新数组空间 

    //统计原数组中元素出现的次数
    for(int i = 0; i < n; i ++) cnt[a[i] - minval] ++;//将元素映射到a[0...d-1] 

    int sum = 0;
    for(int i = 0; i < d; i ++){//本质为前缀和数组,用于求位次 
        sum += cnt[i];//此处的cnt既为元素又为之前的元素和,即cnt[i] = cnt[i] + cnt[i - 1] 
        cnt[i] = sum;// 比如, cnt[5] = 3,表示分数95, 排名第 3 
    } 

    int sortArray[d];//sortArray[]存元素真实序列 
    for(int i = n - 1; i >= 0; i --){//将原数组元素从后往前遍历 
        sortArray[cnt[a[i] - minval] - 1] = a[i];
        cnt[a[i] - minval] --;
    }

    //将排序后的序列赋给原数组
    for(int i = 0, k = 0; i < d; i ++){
        data[k ++] = sortArray[i];
    }
}

完整代码

#include <iostream> 
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <fstream>

using namespace std;
const int N = 200;//注意数组越界问题,开大点 

int num;
int data[N],idx;

//二次优化 
void CountSort(int a[], int n){
    //遍历数组求得最大值和最小值
    int minval = a[0], maxval = a[0];
    for(int i = 0; i < n; i ++){ 
        minval = min(minval, a[i]);
        maxval = max(maxval, a[i]);
    }

    int d = maxval - minval + 1;// 计数数组的实际长度 
    int cnt[d] = {0};//根据最大值开辟新数组空间 

    //统计原数组中元素出现的次数
    for(int i = 0; i < n; i ++) cnt[a[i] - minval] ++;//将元素映射到a[0...d-1] 

    int sum = 0;
    for(int i = 0; i < d; i ++){//本质为前缀和数组,用于求位次 
        sum += cnt[i];//此处的cnt既为元素又为之前的元素和,即cnt[i] = cnt[i] + cnt[i - 1] 
        cnt[i] = sum;// 比如, cnt[5] = 3,表示分数95, 排名第 3 
    } 

    int sortArray[d];//sortArray[]存元素真实序列 
    for(int i = n - 1; i >= 0; i --){//将原数组元素从后往前遍历 
        sortArray[cnt[a[i] - minval] - 1] = a[i];
        cnt[a[i] - minval] --;
    }

    //将排序后的序列赋给原数组
    for(int i = 0, k = 0; i < d; i ++){
        data[k ++] = sortArray[i];
    }
}

int main(){
    //打开文件 
    ifstream infile;
    infile.open("D:\\学习\\数据结构\\第8章排序\\in.txt", ios::in);

    //写文件 
    ofstream outfile;
    outfile.open("D:\\学习\\数据结构\\第8章排序\\out.txt", ios::out);

    if(!infile.is_open()){//判断文件打开是否成功 
        cout << "file open failure!" << endl;
    }

    infile >> num;//读取元素个数 
    while(num --){//将文件中的元素复制到data[1...n] 数组中
        infile >> data[idx ++];
    }

    cout << "排序前元素序列：" << endl;
    for(int i = 0; i < idx; i ++) cout << data[i] << ' '; cout << endl;

    //cout << "使用sort函数排序后序列: " << endl;
    //sort(data, data + idx); 
    //for(int i = 0; i < idx; i ++) cout << data[i] << ' '; cout << endl;

    CountSort(data, idx);
    cout << "使用计数排序后序列为：" << endl;
    for(int i = 0; i < idx; i ++) cout << data[i] << ' '; cout << endl;

    num = idx, idx = 0, outfile << num << endl;//写入数据数num以及在行末写入\n 
    while(num --){
        outfile << data[++ idx] << ' ';//将排序后的数据写到文件中 
    }
    outfile << endl;//向文件末尾写入\n结束符 

    //关闭文件 
    infile.close();
    outfile.close();
    return 0;
}

输入数据(in.txt)

10
13 69 86 99 59 23 64 32 86 72

输出数据(out.txt)

10
13 23 32 59 64 69 72 86 86 99