原文地址:
标题 https://www.cnblogs.com/fallingdust/p/14333402.html
前置知识
主席树:用于处理 历史版本问题:需要以优秀复杂度来解决可持久化问题的数据结构。
可持久化问题(数据结构):
1.部分可持久化:所有版本都可以访问,但是只有最新版本可以修改。
2.完全可持久化:所有版本都既可以访问又可以修改。
初步介绍
主席树:全称可持久化权值线段树,用函数式手法实现可持久化,函数式线段树 是指使用函数式编程思想的线段树。在函数式编程思想中,将计算机运算视为数学函数,并避免可改变的状态或变量。不难发现,函数式线段树是完全可持久化的。
引入:考虑一个例题:区间第k小–给定一个1到n的区间和区间内的值,求出[l,r]内第k小数。
解决方案
为什么主席树可以解决和个问题呢?主席树的主要思想就是:保存每次插入操作时的历史版本,以便查询区间第k小。见例子与图:
假设我们的数列为1 5 2 3 7 6 4
先将其离散化(原因:为保证不超出空间限制,并且:主席树只在乎数字的大小,后文会详细介绍)。用离散的数组建立一棵空树:
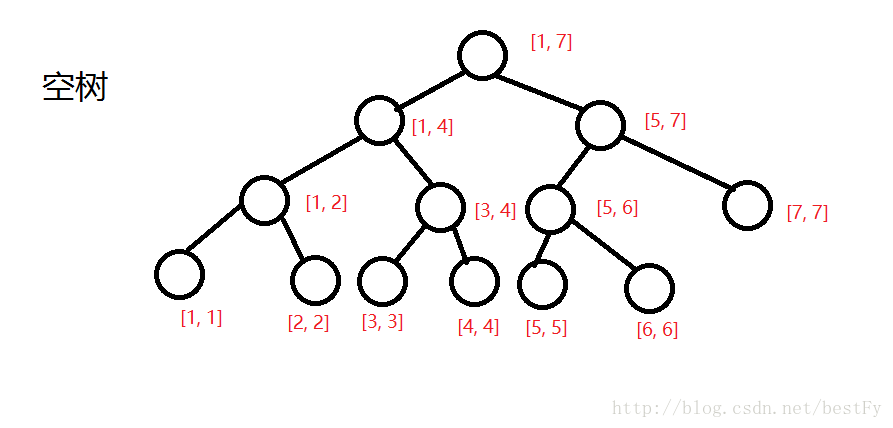
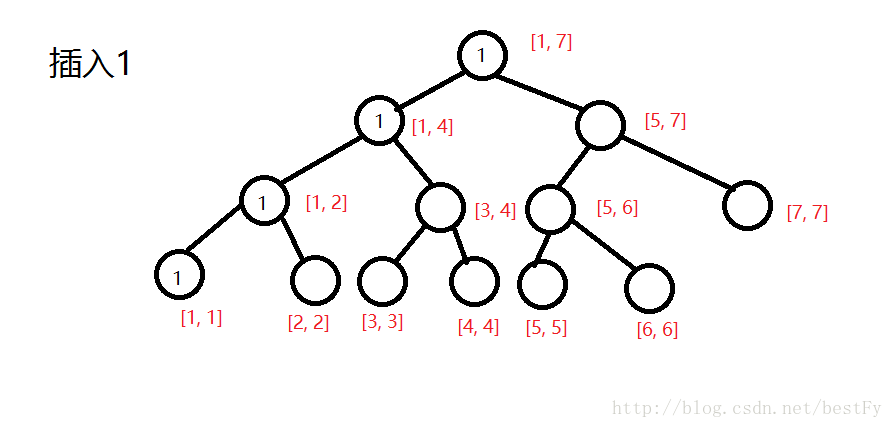
然后将原数组中的树一个个插入树中,并将包含此数字的节点的sum都++:
注意:主席树每个节点保存的信息是:从离散化之后排在l的数字到离散化后排在r的数字一共出现的次数。
离散化的意义:将原数组巨大的数字,以映射的思想,将其按大小转化为1,2,3......这样可以节省空间,当然,如果你愿意用链表那也是完全OK的。<_<
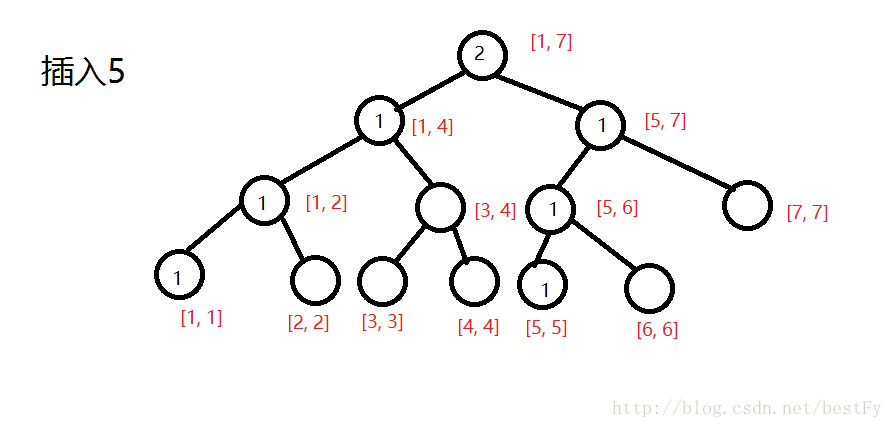
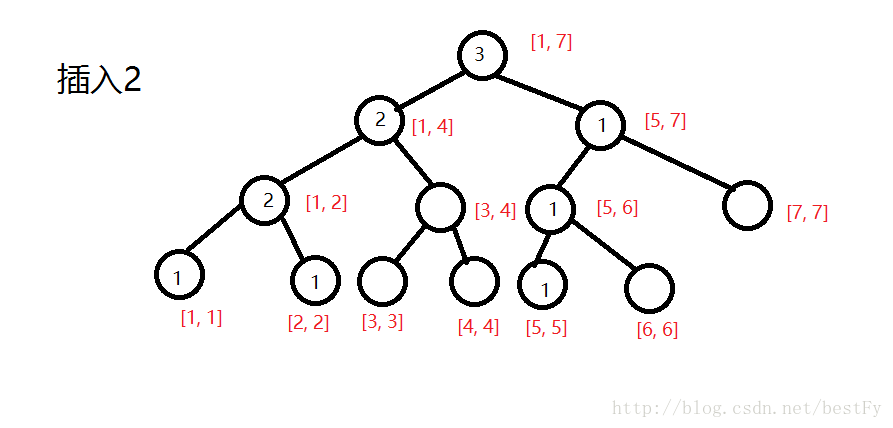
......中间步骤省略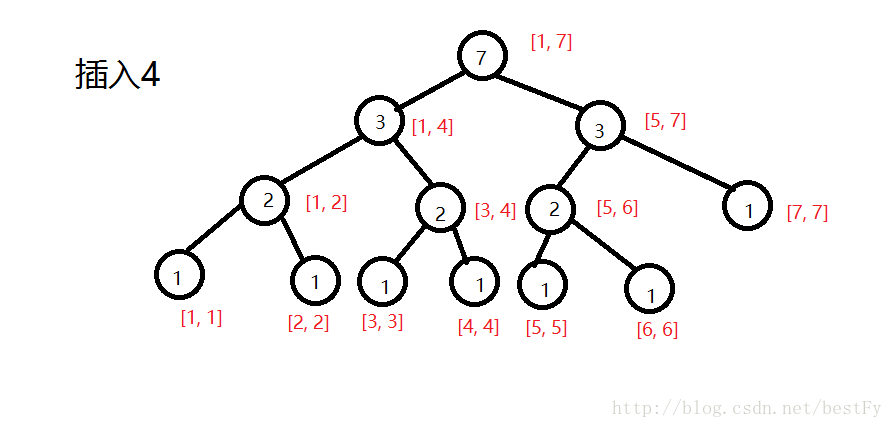
那现在的问题就是:我们如何进行可持久化操作?假设我们要查询[2,5]中第2大的数,考虑:如果你有一个函数,你要求出f(5)-f(2)的值,你会怎么做?主席树是一样的,我们拿出第5次和第2此的版本,把每个节点的sum相减(没错,这就是前缀和思想,每个系欸但存储信息有单调性,并且:详见后恰好就是中间插入带来的贡献,可以自己脑补一下,相信你已经理解了。),剩下的树就是中间3次插入带来的贡献。
考虑查询操作:从根,向下查询,如果当前左子树的大小比要查询的k小,那么向右,反之向左,原因:左子树存的是1到mid这些大小的数字出现次数,如果次数大于k,说明我们的答案在这之中(很好理解),于是,我们就可以用$log_2n$的复杂度解决查询问题,但是问题来了:我们还没有实现可持久化。
持久化操作
请在此观察之前修改的图:我们发现,每次插入,之后$log_2n$的节点会被修改,所以:我们新建根之后,只用再次修改与插入值相关的点就行了,不用每次都建立线段树。
1.建立一棵空树
2.进行原数组插入时,从空树最后一个节点的节点编号tot+1,建立一个新的节点,然后遍历需要修改的节点,不用修改的直接连起来,就可以解决持久化问题。同时,注意:我们需要建立一个时间轴(数组),保存修改节点根的顺序。
相关代码:
inline int update(int pre, int l, int r, int x){
int rt = ++ tot;
L[rt] = L[pre]; R[rt] = R[pre]; sum[rt] = sum[pre] + 1;
if (l < r){
if (x <= mid) L[rt] = update(L[pre], l, mid, x);
else R[rt] = update(R[pre], mid+1, r, x);
}
return rt;
}
int main(){
······
for (int i=1;i<=n;i++){
a[i] = lower_bound(b+1, b+1+m, a[i]) - b;
//找到插入值在离散化后的位置
T[i] = update(T[i-1], 1, m, a[i]);
//T数组保存的就是每次修改的根的编号
}
}
完整代码:
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<cmath>
#include<cctype>
#include<vector>
#include<map>
#include<queue>
using namespace std;
typedef long long LL;
const int N = 200010, LOG = 20;
//一般我们用20倍空间来保存(防止溢出)
int n, m, q, tot = 0;
//tot就是时间戳(每个节点的编号)
int a[N], b[N];
int T[N], sum[N*LOG], L[N*LOG], R[N*LOG];
//建树
inline int build(int l, int r){
int rt = ++ tot;
int mid=l+r>>1;
if (l < r){
L[rt] = build(l, mid);
R[rt] = build(mid+1, r);
}
return rt;
}
//更新
inline int update(int pre, int l, int r, int x){
int rt = ++ tot;
L[rt] = L[pre]; R[rt] = R[pre]; sum[rt] = sum[pre] + 1;
if (l < r){
int mid=l+r>>1;
//按离散化有的编号进行更新
if (x <= mid) L[rt] = update(L[pre], l, mid, x);
else R[rt] = update(R[pre], mid+1, r, x);
}
return rt;
}
//查询操作
inline int query(int u, int v, int l, int r, int k){
if (l == r) return l;
int x = sum[L[v]] - sum[L[u]];
//x就是左子树的大小
int mid=l+r>>1;
if (x >= k) return query(L[u], L[v], l, mid, k);
else return query(R[u], R[v], mid+1, r, k-x);
}
int main(){
int t;
tot=0;
memset(T, 0, sizeof T);
memset(sum, 0, sizeof sum);
memset(L, 0, sizeof L);
memset(R, 0, sizeof R);
scanf("%d%d",&n,&q);
for (int i=1;i<=n;i++)
scanf("%d", &a[i]), b[i] = a[i];
sort(b+1, b+1+n);
m = unique(b+1, b+1+n)-b-1;
T[0] = build(1, m);
for (int i=1;i<=n;i++){
a[i] = lower_bound(b+1, b+1+m, a[i]) - b;
//查找离散后的下标
T[i] = update(T[i-1], 1, m, a[i]);
//增加时间,用来查询历史
//printf ("a[%d]=%d,T[%d]=%d\n",i,a[i],i,T[i]);
}
while (q --){
int x, y, z;
scanf("%d%d%d", &x, &y, &z);
int p = query(T[x-1], T[y], 1, m, z);
printf("%d\n", b[p]);
}
return 0;
}

