# 排序

快速排序

核心–>分治

主要思想：在一个数组中任意取一数作为分界点x（一般取q[l+r＞＞1]不容易出现边界问题），通过调整使得数组左边的数满足小于等于x，右边的数大于等于x，然后不断递归处理左右两段，直至区间有序

方法：
1:确定分界点(当前区间内随机一个数组里的值)
2:调整区间
3:递归处理左右两段

模板：

void quick_sort(int q[], int l, int r)
{
if (l >= r) return;`
int i = l - 1, j = r + 1, x = q[l + r >> 1];
while (i < j)
{
do i ++ ; while (q[i] < x);
do j – ; while (q[j] > x);
if (i < j) swap(q[i], q[j]);
}
quick_sort(q, l, j), quick_sort(q, j + 1, r);
}
// 模板需注意以下几点

1：i，j双指针定义的时候需往外扩1格;
2：当i，j两个指针相遇时循环结束，while里的判断条件为q[i]<x和q[j]>x;
   当i，j两个指针穿过时循环结束，while里的判断条件为q[i]<=x和q[j]>=x;
3：递归处为quick_sort(q,l,j),quick_sort(q,j+1,r)时，分界点x不能取q[r];
   递归处为quick_sort(q,l,i-1),quick_sort(q,i,r)时，分界点x不能取q[l];

归并排序

核心：分治

主要思想：在一个数组中以数组下标的中间值的位置为分界点，通过不断递归左右两段使得数组左右两段分别有序，最后归并使得整个数组有序

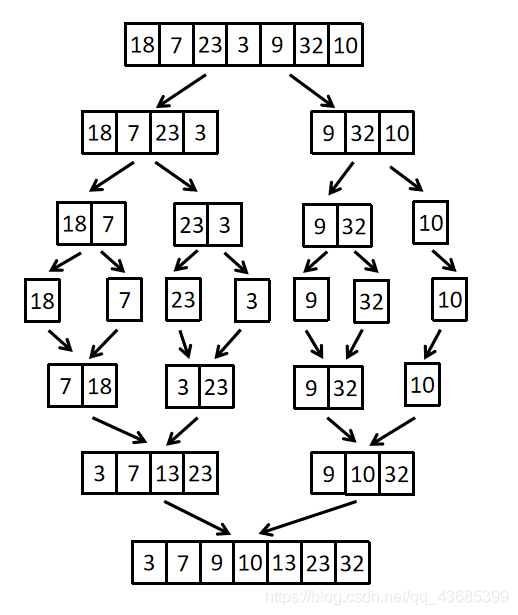
方法：
1：确定分界点（数组下标的中间位置）
2：递归排序
3：归并——合二为一

模板:

void merge_sort(int q[], int l, int r)
{
    if (l >= r) return;

    int mid = l + r >> 1;
    merge_sort(q, l, mid);
    merge_sort(q, mid + 1, r);

    int k = 0, i = l, j = mid + 1;
    while (i <= mid && j <= r)
        if (q[i] <= q[j]) tmp[k++] = q[i++];
        else tmp[k++] = q[j++];
    while (i<= mid) tmp[k++] = q[i++];
    while (j<= r) tmp[k++] = q[j++];

    for (i = l, j = 0; i <= r; i++,j ++) q[i] = tmp[j];
}

// 补充

//两种排序方法的时间复杂度和稳定性

时间复杂度：n*log n

稳定性：

快速排序—不稳定
递归排序—稳定

# 二分

主要思想：如果能在一段区间上定义某种性质，使得区间分为满足性质和不满足性质两部分，那么我们可以通过二分的思想将两部分不在端点处的边界点求出

//一般二分是一定有解的，只是可能题目无解

整数二分

方法：
1：确定中间值mid
2：判断mid是否满足性质，更新区间，直到区间端点重合退出循环（此时的端点的值即为所求边界点）

模板：

bool check(int x) {/* ... */} // 检查x是否满足某种性质

// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用：
int bsearch_1(int l, int r)
{
    while (l < r)
    {
        int mid = l + r >> 1;
        if (check(mid)) r = mid;    // check()判断mid是否满足性质
        else l = mid + 1;
    }
    return l;
}
// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用：
int bsearch_2(int l, int r)
{
    while (l < r)
    {
        int mid = l + r + 1 >> 1;
        if (check(mid)) l = mid;
        else r = mid - 1;
    }
    return l;
}

//两种模板记忆技巧：
当更新区间时，如果是l=mid，则mid=1+r+1>>1(不加1可能会死循环）,r=mid,则mid=l+r>>1

浮点数二分

模板：

bool check(double x) {/* ... */} // 检查x是否满足某种性质

double bsearch_3(double l, double r)
{
    const double eps = 1e-6;   // eps 表示精度，取决于题目对精度的要求
    while (r - l > eps)
    {
        double mid = (l + r) / 2;
        if (check(mid)) r = mid;
        else l = mid;
    }
    return l;
}

//注意

浮点数二分时eps的值最好比要求的精度高两级以免产生精度问题