拓扑序列

图的拓扑序列针对于有向图

若一个由图中所有点构成的序列 A 满足：对于图中的每条边 (x,y)，x 在 A 中都出现在 y 之前，则称 A 是该图的一个拓扑序列。（所有边都是从前指向后的）

图中有环则一定不存在拓扑序列

有向图中点的入度: 一个点有多少条边指向自己
有向图中点的入度：一个点有多少条边出去

拓扑序列中，所有入度为0的点均可以作为起点
有向无环图一定至少存在一个入度为0的点

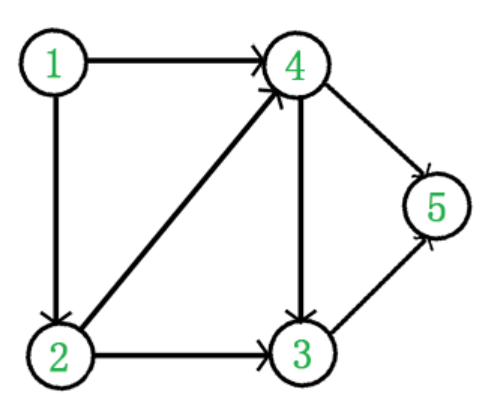
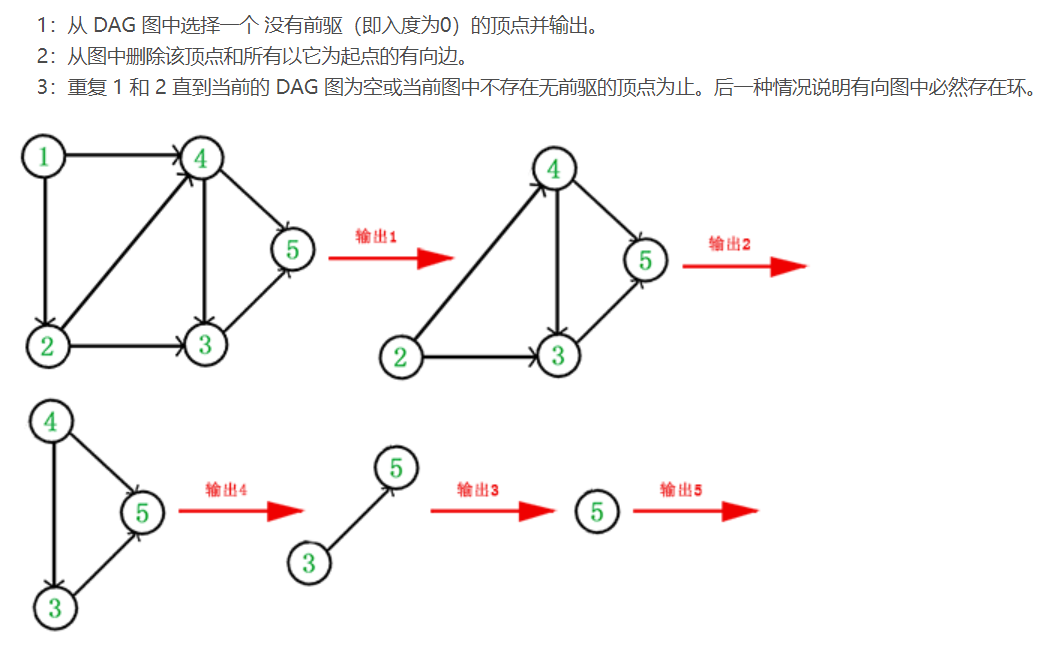
所有入度为0的点入队 -> queue
while( 队列不空 ) {
    队头 ——> t
    枚举t的所有出边 t ——> j
    // d[] 表示出度
    删除t ——> j ( d[j] -- )
    if( d[j] == 0 ) 
       j ——> queue // j入队
}

拓扑排序：

bool topsort()
{
    int hh = 0, tt = -1;

    // d[i] 存储点i的入度, 点编号由1到n
    for (int i = 1; i <= n; i ++ )
        if (!d[i])
            q[ ++ tt] = i;

    while (hh <= tt)
    {   
        // 队列中q的次序恰好为拓扑排序
        int t = q[hh ++ ];
        for (int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            d[j]--;
            if ( d[j] == 0 ) q[ ++ tt] = j;
        }
    }
    // 如果所有点都入队了，说明存在拓扑序列；否则不存在拓扑序列。
    return tt == n - 1;
}

输入时：

cin >> n >> m;
memset(h,-1,sizeof(h));
for ( int i =0; i<m; i++ ) {
    int a,b;
    cin >> a >> b;
    add(a,b);
    d[b]++; // 入度增加
}