二进制位运算

加法

  00001101
+ 00010011
= 00100000

减法

  00001101
- 00000011
= 00001010

与

  00001101
& 00000011
= 00000001

或

  00001101
| 00000011
= 00001111

异或

  00001101
^ 00000011
= 00001110

右移位>>3

  00001101>>3
= 00000001

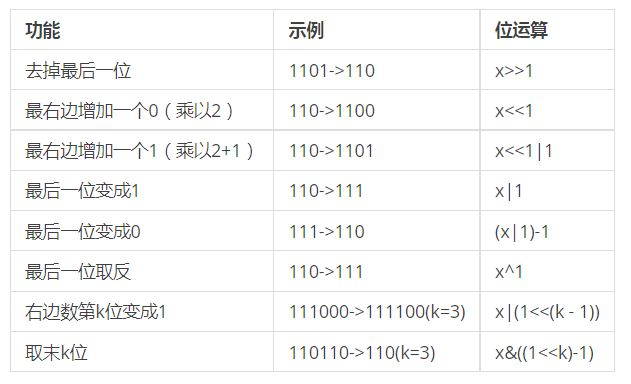
技巧

例题1：Traveling Salesman among Aerial Cities

本题是经典的 TSP问题

记 dp[S][v] 表示已经访问过的城市集合为 $S$ 且最后一个访问的城市是 $v$ 的最小花费

Code:

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using namespace std;

inline void chmin(int& x, int y) { if (x > y) x = y; }

int main() {
    int n;
    cin >> n;

    vector<int> x(n), y(n), z(n);
    rep(i, n) cin >> x[i] >> y[i] >> z[i];

    int n2 = 1<<n;
    const int INF = 1001001001;
    vector dp(n2, vector<int>(n, INF));
    vector dist(n, vector<int>(n));
    rep(i, n)rep(j, n) {
        int now = abs(x[i]-x[j]);
        now += abs(y[i]-y[j]);
        now += max(0, z[j]-z[i]);
        dist[i][j] = now;
    }
    for (int i = 1; i < n; ++i) {
        dp[1<<i][i] = dist[0][i];
    } 

    rep(s, n2)rep(v, n) {
        if (~s>>v&1) continue;
        rep(u, n) {
            if (s>>u&1) continue;
            chmin(dp[s|1<<u][u], dp[s][v]+dist[v][u]);
        }
    }

    cout << dp[n2-1][0] << '\n';

    return 0;
}

例题2：[USACO06NOV]Corn Fields G link

农夫约翰的土地由 $M \times N$ 个小方格组成，现在他要在土地里种植玉米。
非常遗憾，部分土地是不育的，无法种植。
而且，相邻的土地不能同时种植玉米，也就是说种植玉米的所有方格之间都不会有公共边缘。
现在给定土地的大小，请你求出共有多少种种植方法。
土地上什么都不种也算一种方法。
制约：$1 \leqslant N, M \leqslant 12$

分析：

每行土地看做一个状态，把输入的数据每行压缩成一个整数

for (int i = 1; i <= m; ++i) {
    status = 0;
    for (int j = 1; j <= n; ++j) {
        cin >> t;
        status = (status << 1) + t;
    }
    field[i] = status;
}

每行草的情况也看成是一个二进制整数，$1$ 表示种草，$0$ 表示不种。合法的状态满足条件
$(k \& (k >> 1)) == 0$

ll dp[MAXN][1<<13]; // dp[i][j]表示考虑到第i行，状态编号为j的时候，方案数 
dp[i][j] = dp[i][j] + dp[i - 1][k]; // k和j不能冲突 

Code:

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using std::cin;
using std::cout;
using std::istream;
using std::ostream;
using ll = long long;

// const int mod = 998244353;
//const int mod = 1000000007;
const int mod = 100000000;
struct mint {
    ll x;
    mint(ll x=0):x((x%mod+mod)%mod) {}
    mint operator-() const {
        return mint(-x);
    }
    mint& operator+=(const mint a) {
        if ((x += a.x) >= mod) x -= mod;
        return *this;
    }
    mint& operator-=(const mint a) {
        if ((x += mod-a.x) >= mod) x -= mod;
        return *this;
    }
    mint& operator*=(const mint a) {
        (x *= a.x) %= mod;
        return *this;
    }
    mint operator+(const mint a) const {
        return mint(*this) += a;
    }
    mint operator-(const mint a) const {
        return mint(*this) -= a;
    }
    mint operator*(const mint a) const {
        return mint(*this) *= a;
    }
    mint pow(ll t) const {
        if (!t) return 1;
        mint a = pow(t>>1);
        a *= a;
        if (t&1) a *= *this;
        return a;
    }

    // for prime mod
    mint inv() const {
        return pow(mod-2);
    }
    mint& operator/=(const mint a) {
        return *this *= a.inv();
    }
    mint operator/(const mint a) const {
        return mint(*this) /= a;
    }
};
istream& operator>>(istream& is, mint& a) {
    return is >> a.x;
}
ostream& operator<<(ostream& os, const mint& a) {
    return os << a.x;
}

const int MX = 15;
int field[MX];
int valid[1 << 13];
int validCount;
mint dp[MX][1 << 13];

int main() {
    int m, n, t, status;
    cin >> m >> n;
    for (int i = 1; i <= m; ++i) {
        status = 0;
        for (int j = 1; j <= n; ++j) {
            cin >> t;
            status = (status << 1) + t;
        }
        field[i] = status;
    }

    int n2 = 1 << n;
    rep(k, n2) { // 筛出草的所有合法状态 
        if ((k & (k >> 1)) == 0) {
            valid[validCount++] = k;
        }
    }

    rep(i, validCount) {
        status = valid[i];
        if ((status & field[1]) == status) { // 当前的草和土是否冲突, 草是1，对应的土地也需要是1 
            dp[1][i] = 1;
        }
    }

    for (int i = 2; i <= m; ++i) {
        rep(j, validCount) {
            int j2 = valid[j];
            if ((j2 & field[i]) == j2) {
                rep(k, validCount) {
                    int k2 = valid[k];
                    if ((j2 & k2) == 0) { // 检测当前一行草的状态和上一行的草的状态是否有冲突 
                        dp[i][j] += dp[i - 1][k];
                    } 
                }
            }
        }
    }

    mint ans;
    rep(i, validCount) ans += dp[m][i];

    cout << ans << '\n';

    return 0;
} 

例3：[SCOI2005]互不侵犯 link

在 $N×N$ 的棋盘里面放K个国王，使他们互不攻击，共有多少种摆放方案。国王能攻击到它上下左右，以及左上左下右上右下八个方向上附近的各一个格子，共 $8$ 个格子。
制约：$1 \leqslant N \leqslant 9, 0 \leqslant K \leqslant N \times N$

0101 表示：这一行的第一个格子没有国王，第二个格子放了国王，第三个格子没有放国王，第四个格子放了国王

合法状态 if((i & (1<<i)) == 0)，注意 == 运算的优先级比 $\&$ 高，要加括号

数合法状态中的国王的个数

int count1(int a) {
    int r = 0;
    while (a) {
        r += a & 1;
        a >>= 1;
    }
    return r;
}

等价于C++中的 __builtin_popcount()

dp[i][j][x] // 表示考虑前 i 行，状态的编号为 j, 包含这行总共 x 个国王有多少种放法
ll dp[10][SIZE][85] // SIZE: 表示合法状态的个数

Code:

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using std::cin;
using std::cout;
using ll = long long;

#define SIZE 1024
int valid[SIZE]; // 保存所有合法状态
int count[SIZE]; // 每个合法状态中有几个国王
int nextValid; // 下一个合法状态下标 
ll dp[10][SIZE][90];

int main() {
    int n, k;
    cin >> n >> k;

    int n2 = 1 << n;
    rep(i, n2) {
        if ((i & (i<<1)) == 0) {
            valid[nextValid] = i;
            count[nextValid] = __builtin_popcount(i);
            nextValid++;
        }
    }

    rep(i, nextValid) dp[1][i][count[i]] = 1;

    for (int i = 2; i <= n; ++i) {
        rep(j, nextValid) {
            int j2 = valid[j];
            rep(x, nextValid) {
                int x2 = valid[x];
                if ((j2 & x2) == 0 and ((j2 << 1) & x2) == 0 and (j2 & (x2 << 1)) == 0) {
                    for (int y = count[j]; y <= k; ++y) { // 统计到当前行为止放了多少个国王 
                        dp[i][j][y] += dp[i - 1][x][y - count[j]];
                    }
                }
            }
        }
    }

    ll ans = 0;
    rep(i, nextValid) ans += dp[n][i][k];

    cout << ans << '\n';

    return 0;
}

例4：蒙德里安的梦想 link

求把 $N×M$ 的棋盘分割成若干个 $1×2$ 的的长方形，有多少种方案。
制约：$1 \leqslant n, m \leqslant 11$

分析：

我们考虑按列摆放，某列的各行用 $0$ 或 $1$ 表示摆放状态
如果某行是 $1$，表示横放，并且向下一列伸出
如果某行是 $0$，表示竖放，并且由前一列伸出

1. 状态表示：f[i][j] 表示摆放第 $i$ 列，状态为 $j$ 时的方案数
   状态转移：$f[i-1][k] \to f[i][j]$
2. 状态计算：$f[i][j] = \sum f[i - 1][k]$
3. 初值：$f[0][0] = 1$，其他为 $0$
4. 答案：$f[m][0]$

Code：

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)
#define rrep(i, n) for (int i = 1; i <= (n); ++i)

using std::cin;
using std::cout;
using ll = long long; 

int n, m;
bool st[1<<12]; // st[i] 存储合并列的状态 i 是否合法
ll f[12][1<<12]; // f[i][j] 表示摆放第 i 列，状态为 j 时的方案数 

int main() {
    while  (cin >> n >> m, n or m) {
        // 预处理：判断合并列的状态 i 是否合法
        // 如果合并列的某行是 1 表示横放，是 0 表示竖放
        // 如果合并列不存在连续的奇数个 0，即为合法 
        int n2 = 1 << n;
        rep(i, n2) {
            st[i] = true;
            int cnt = 0; // 记录合并列中连续 0 的个数
            rep(j, n) {
                if (i>>j & 1) {
                    if (cnt & 1) { // 如果连续 0 的个数是奇数 
                        st[i] = false;
                        break;
                    }
                }
                else cnt++; // 如果是 0，记录 0 的个数 
            } 
            if (cnt & 1) st[i] = false; // 处理高位 0 的个数 
        }

        // 状态计算
        std::memset(f, 0, sizeof f);
        f[0][0] = 1; // 第 0 列不横放是一种合法的方案 
        rrep(i, m) { // 阶段：枚举列 
            rep(j, n2) { // 状态：枚举第 i 列的状态 
                rep(k, n2) { // 状态：枚举第 i - 1 列的状态 
                    // 两列状态兼容：不出现重叠的 1，不出现连续的奇数个 0
                    if ((j & k) == 0 and st[j | k]) {
                        f[i][j] += f[i - 1][k]; // 前一列兼容状态的方案数之和 
                    }
                }
            } 
        }

        cout << f[m][0] << '\n'; // 第 m 列不横放，即答案 
    } 

    return 0;
}

例5：炮兵阵地 link

分析：

1. 行内合法：如果 $!(i \& i >> 1)$ 且 $!(i \& i >> 2)$ 为真，则 $i$ 合法
2. 行间合法：如果 $!(a \& b)$ 且 $!(b \& c)$ 且 $!(b \& c)$ 且 $(a \& g[i] == a)$ 为真，则 $a, b, c$ 合法
3. 状态表示：f(i, a, b) 表示已摆放前 $i$ 行，当前是第 $i$ 行为第 $a$ 个状态，并且上一行是第 $b$ 个状态时，能摆放的最大数量
   $f(i - 1, b, c) + num[a] \to f(i, a, b)$
4. 状态计算：$f(i, a, b) = \max(f(i, a, b), f(i - 1, b, c) + num[a])$
5. 边界：$f() = 0$
6. 最大数量：$\max(f(n, a, b))$

注：可以考虑用 滚动数组 优化空间，因为第 $i$ 行只跟第 $i - 1$ 行的状态有关，所以第一维只开 $2$ 个空间就够了

C++ 代码

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)
#define rrep(i, n) for (int i = 1; i <= (n); ++i)

using std::cin;
using std::cout;

const int N = 105, M = 1<<10;

int n, m;
int g[N]; // 保存地图各行数值
int cnt; // 同一行的合法状态个数
int s[N]; // 同一行的合法状态集
int num[M]; // 每个合法状态包含 1 的个数
int f[2][M][M]; // f[i][a][v] 表示已放好前 i 行，第 i 行第 a 个状态，第 i-1 行第 b 个状态时，能放置的最大数量 

void chmax(int &x, int y) { if (x < y) x = y; }

int main() {
    cin >> n >> m;

    // 预处理地图
    rrep(i, n)rep(j, m) {
        char c; cin >> c;
        if (c == 'P') g[i] += 1 << (m - j - 1); // 保存地图各行数值 
    }

    // 预处理合法状态
    rep(i, 1<<m) { // 枚举每一行的所有状态 
        if (!(i&i>>1) and !(i&i>>2)) { // 如果不存在 11 或 101 
            s[cnt++] = i;
            rep(j, m) {
                num[i] += (i>>j&1); // 统计合法状态包含 1 的个数 
            }
        }
    } 

    // 状态计算
    rrep(i, n + 2) { // 枚举行 
        rep(a, cnt) { // 枚举第 i 行合法状态 
            rep(b, cnt) { // 枚举第 i-1 行合法状态 
                rep(c, cnt) { // 枚举第 i-2 行合法状态 
                    if (!(s[a]&s[b]) and !(s[a]&s[c]) and !(s[b]&s[c])
                    and (g[i]&s[a]) == s[a] and (g[i - 1]&s[b]) == s[b]) {
                        chmax(f[i&1][a][b], f[i - 1 & 1][b][c] + num[s[a]]);
                    }
                }
            }
        }
    } 

    cout << f[n + 2 & 1][0][0] << '\n';

    return 0;
}

例6: 排列 link

给一个数字串 $s$ 和正整数 $d$, 统计 $s$ 有多少种不同的排列能被 $d$ 整除（可以有前导 $0$）。例如 $123434$ 有 $90$ 种排列能被 $2$ 整除，其中末位为 $2$ 的有 $30$ 种，末位为 $4$ 的有 $60$ 种。
制约：

• $|s| \leqslant 10$
• $1 \leqslant d \leqslant 1000$
• $1 \leqslant T \leqslant 15$

分析：

记 f[sta][p] 表示已经使用的数字的状态为 sta，现在数字模 d 的结果为 p，每次找到 $sta$ 里面还没放进去的一个数字，然后放进去，$p = p * 10 + x$，取模后更新即可。
不过这个题问的是最后有多少种方案，是考虑顺序的。相同元素顺序被重复计数了，所以要记得除掉对应元素个数的阶乘。

Code：

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using std::cin;
using std::cout;
using std::string;
using std::vector;

int f[1<<12][1010];

int main() {
    int t;
    cin >> t;

    while (t--) {
        std::memset(f, 0, sizeof f);

        string s;
        cin >> s;
        int n = s.size();
        int d;
        cin >> d;

        vector<int> a(n);
        rep(i, n) a[i] = s[i] - '0';
        vector<int> cnt(10);
        rep(i, n) cnt[a[i]]++; 

        int n2 = 1 << n;
        f[0][0] = 1;
        rep(i, n2) {
            rep(j, d) {
                if (f[i][j]) {
                    rep(k, n) {
                        if ((i & (1<<k)) == 0) {
                            f[i | (1<<k)][(j * 10 + a[k]) % d] += f[i][j];
                        }
                    }
                }
            }
        }

        int ans = f[n2 - 1][0];
        rep(i, 10) {
            while (cnt[i] > 1) {
                ans /= cnt[i];
                --cnt[i];
            }
        }
        cout << ans << '\n';
    }

    return 0;
}