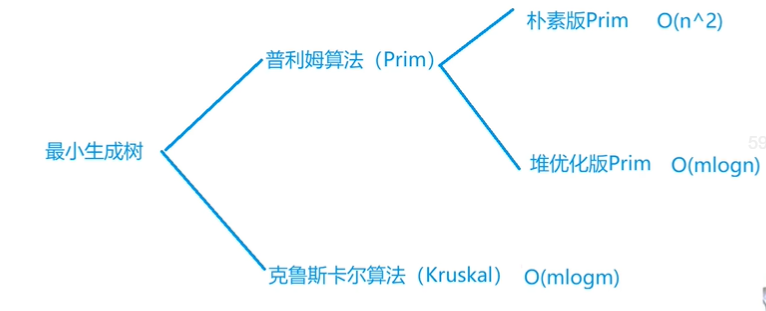
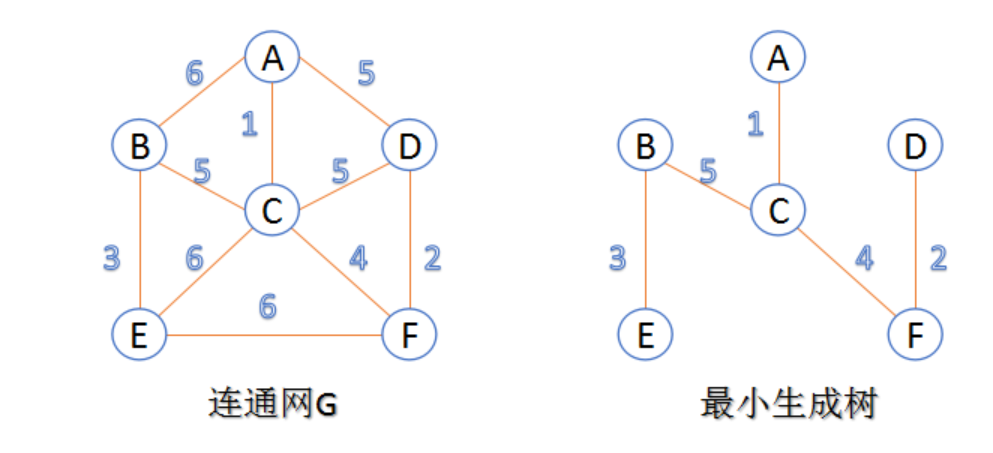
最小生成树: 图中选中所有距离最小的边组成的树型结构

朴素Prim ——> 稠密图
堆优化Prim ——> 稀疏图( 不常用 )
Kruskal ——> 稀疏图

朴素Prim算法 —— O( n^2 + m )

集合s: 当前已经在连通块中的所有点
// 点到集合的距离: 这个点可以连到集合当中的所有边中，长度最小的边
+∞ ——> dist[i] // 所有点到集合的距离 初始化为正无穷 
// n次迭代
for(int i = 0; i < n; i++ ) {

    找到集合外距离最近的点 ——> t
    用t更新其他点到集合的距离
    st[t] = true;
}

算法实现：

int n;      // n表示点数
int g[N][N];        // 邻接矩阵，存储所有边(稠密图)
// g的初始化：memset(g,0x3f, sizeof(g));
int dist[N];        // 存储其他点到当前最小生成树的距离
bool st[N];     // 存储每个点是否已经在生成树中


// 如果图不连通，则返回INF(值是0x3f3f3f3f), 否则返回最小生成树的树边权重之和
int prim( )
{
    memset(dist, 0x3f, sizeof dist);

    int res = 0; // 最小生成树中所有边的权重之和
    for (int i = 0; i < n; i ++ )
    {   
        int t = -1;
        for (int j = 1; j <= n; j ++ )
            if (!st[j] && (t == -1 || dist[t] > dist[j]))
                t = j;

        // 图不连通，最小生成树不存在
        if (i && dist[t] == INF) return INF;

        if (i) res += dist[t]; // dist[t] 表示当前的点与当前生成树中某一条边的长度

                                       // 注意与dijstra算法的区别
                                       // prim中表示这个点到已连接好的生成树集合的最短距离
        for (int j = 1; j <= n; j ++ ) dist[j] = min(dist[j], g[t][j]);
        st[t] = true;
    }

    return res;
}

// 输入
int a,b,c;
cin >> a >> b >> c;
g[a][b] = g[b][a] = min( g[a][b], c ); // 重边取最小（无向图）

Kruskal算法 —— O(mlogm)

将所有边按权重大小从小到大排序 // 以边为主导地位，始终选择当前可用的最小边权的边
枚举每条边a，b, 权重为c{
    if( a，b 不连通 ) 将这条边加入集合
}

算法实现：

int n, m;       // n是点数，m是边数
int p[N];       // 并查集的父节点数组

struct Edge     // 存储边
{
    int a, b, w;
}edges[M];
//按照权值排序，权值小的放前面
bool cmp(Edge x, Edge y) {
    return x.w < y.w;
}

int find(int x)     // 并查集核心操作
{
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int kruskal()
{
    sort(edges, edges + m,cmp);

    for (int i = 1; i <= n; i ++ ) p[i] = i;    // 初始化并查集

    int res = 0, cnt = 0; // res存储最小生成树所有边的权重之和，cnt存储当前加了多少条边
    for (int i = 0; i < m; i ++ )
    {
        int a = edges[i].a, b = edges[i].b, w = edges[i].w;

        a = find(a), b = find(b); // 找到a,b的祖宗结点
        if (a != b)     // 如果两个连通块不连通，则将这两个连通块合并
        {
            p[a] = b; // 合并集合
            res += w;
            cnt ++ ;
        }
    }

    if (cnt < n - 1) return INF; // n-1条边，n个点
    return res;
}