二分图: 图中点可以被分为两组，并且使得所有边都跨越组的边界，则这就是一个二分图。即：可以把图中的点分为两组，每组内部的点没有边相连，只有两组集合之间有边连接，如果存在这样的划分，则此图为一个二分图。

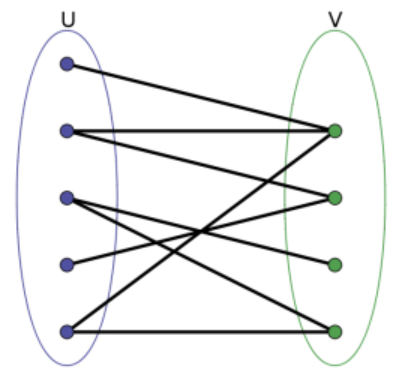
性质：二分图一定不含有奇数环 / 若图不含有奇数环则为二分图

染色法

DFS搜索，将所有点染为黑白二色(一条边的两个端点一定属于不同的集合)
染色过程中若出现矛盾

从前往后遍历所有点
如果当前点还未分好组，将其分到左边
遍历所有与当前点连通的点，与其相连的点分到右边(与右边相连的点分到左边)

for( int i = 1; i <= n; i++ ) {
    if( i 未染色 ) {
        dfs(i); // 用dfs将i所在的连通块都染一遍( 连通块中的一个点确定颜色则所有的点均确定颜色)
    }
}

算法实现：

int n;      // n表示点数
int h[N], e[M], ne[M], idx;     // 邻接表存储图
int color[N];       // 表示每个点的颜色，-1表示未染色，0表示白色，1表示黑色
// 初始化：
memset(h, -1,sizeof(h));
memset(color, -1,sizeof(color));


// 参数：u表示当前节点，c表示当前点的颜色
bool dfs(int u, int c)
{
    color[u] = c; // 记录当前点的颜色
    for (int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i];
        // j还未染色
        // 当前c为白色( 1 )，则将相邻点染为黑色( !c ), 反之染为白色
            // 失败返回false
        if( color[j] == -1 && !dfs(j, !c)) return false;
        // j 点的颜色和当前的颜色相同，出现矛盾(一条边的两点颜色一定不同)
        else if (color[j] == c) return false;
    }
    // 成功，返回ture
    return true;
}
// 判断是否为二分图
bool check()
{
    bool flag = true;
    for (int i = 1; i <= n; i ++ )
        if (color[i] == -1)
            if (!dfs(i, 0)) // 当前这个点还未染色
            {
                flag = false;
                break;
            }
    return flag;
}

匈牙利算法

返回二分图中左右成功匹配的最大数量的大小
成功匹配：不存在两条边共用一个点（没有一个点在多条边上）

int n1, n2;     // n1表示第一个集合中的点数，n2表示第二个集合中的点数

//邻接表存储所有边，匈牙利算法中只会用到从第一个集合指向第二个集合的边，所以这里只用存一个方向的边
int h[N], e[M], ne[M], idx;     
int match[N];       // 存储第二个集合中的每个点当前匹配的第一个集合中的点是哪个
bool st[N];     // 表示第二个集合中的每个点是否已经被遍历过

bool find(int x)
{
    // 枚举一个点所有与其相连的点
    for (int i = h[x]; i != -1; i = ne[i])
    {
        int j = e[i];
        if (!st[j])
        {
            st[j] = true;
            // 相连的点还未匹配 || 可以为这个点找到下一点相连的点
            if (match[j] == 0 || find(match[j]) )
            {
                match[j] = x;
                return true;
            }
        }
    }

    return false;
}

// 求最大匹配数，依次枚举第一个集合中的每个点能否匹配第二个集合中的点
int res = 0;
for (int i = 1; i <= n1; i ++ )
{
    memset(st, false, sizeof st);
    if (find(i)) res ++ ;
}