浅谈tire字典树

1. 从字典到字典树
2. 详解tire数据结构实现
3. tire模板和实战

从字典到字典树

程序和生活中都免不了查找，我们习惯的查找方式一般有两种：

第一种，在学校里的排行榜里头一个一个往下找自己的名字，这个叫做逐个查找，需要的时间复杂度为O(nm),n:排名 ， m:名字长度

第二种，当我们在查字典(先用英语字典理解)的时候，举个例子：Hertz，我们会先在开头字母的ABCD....XYZ里面找到H，然后再在以H为开头的单词中找下一个字母e，以此类推，时间复杂度为O（n）

第一种方法我们可以很简单的用暴力匹配来解决，只需要一一比较。用O(mn)的时间完成就好了

但是，如果我们在查字典的时候，也像上面一样，先翻到第一页，一个单词一个单词的对，可能我们查一年都查不到

而联想我们的第二中找法，我们先找第一个字母，再在以第一个字母开头的单词里找第二个字母，层层推进，省了很大功夫！

而这种一层一层的关系，就是数据结构里面的树结构啊！！

也就是说，你在查字典的时候，就是一个查找树的过程

而字典，其实就是一个排序好的树

对于计算机，如果按表格存，假设每个单词6个字母，有30000个单词，就要存180000个字符，而用tire树，不管多少单词，最多只要存26^6的单词（好像也不少，但是实际上效果很好）

详解tire数据结构的实现

如果认真的话，我们可以把整个字典收集成一个树，像这样：

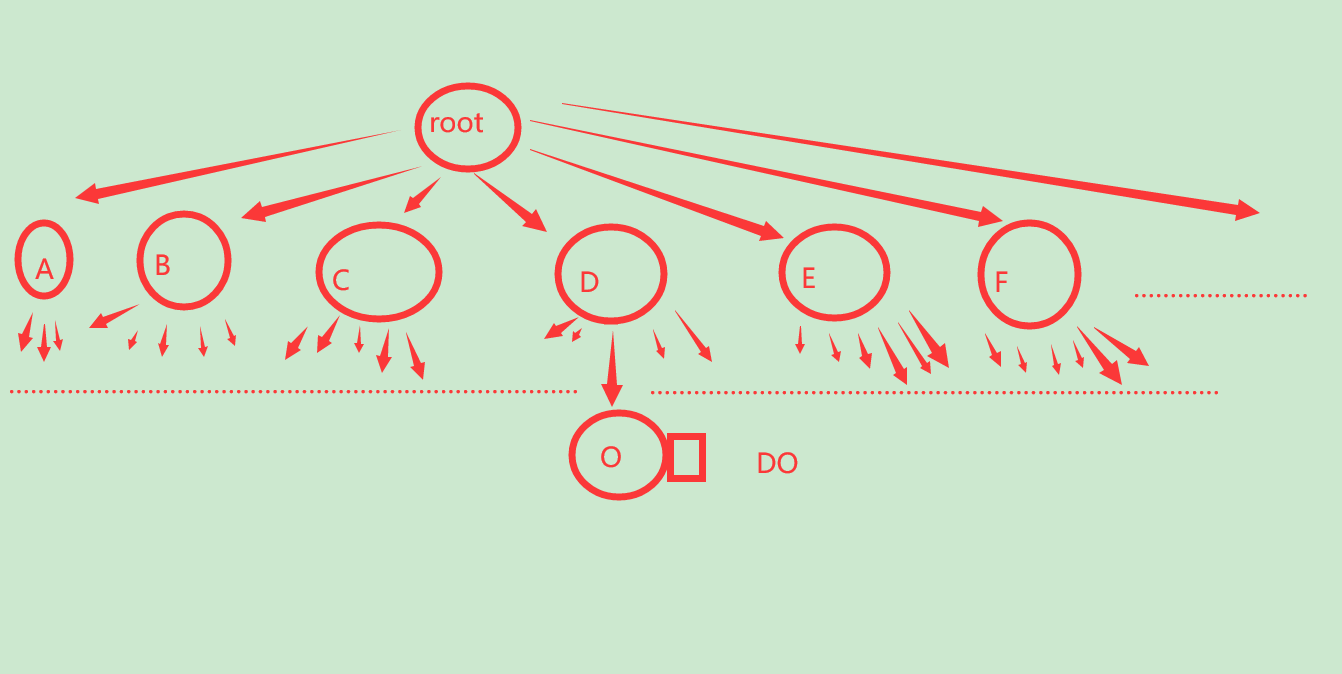
仔细想，这个树都有什么特点？

每个结点保存一个字母作为值（其实也可以用边来表示，但是用结点更方便）

注意到我们留出的do，我们在o的旁边标记了一个矩形，实际上，我们会用这个矩形表示从根节点到该点的路径存在该单词！

而我们利用的字典就是这个道理生成的，我们把所有单词都加到这个树（按字典序）里面，然后一套BFS，就可以得到按字典序排序的所有单词，而因为它经过了排序，我们也就可以轻松的查询了

当然字典树的用处不止于此，接下来我们先复刻一遍单词加入字典树的过程，感受一下字典树是怎么构造的

首先，空空如也的开始：

然后，我们开始一个一个插入单词！
假设我们只要插入：
cat
car
com
OK

我们一个一个来：
首先，cat

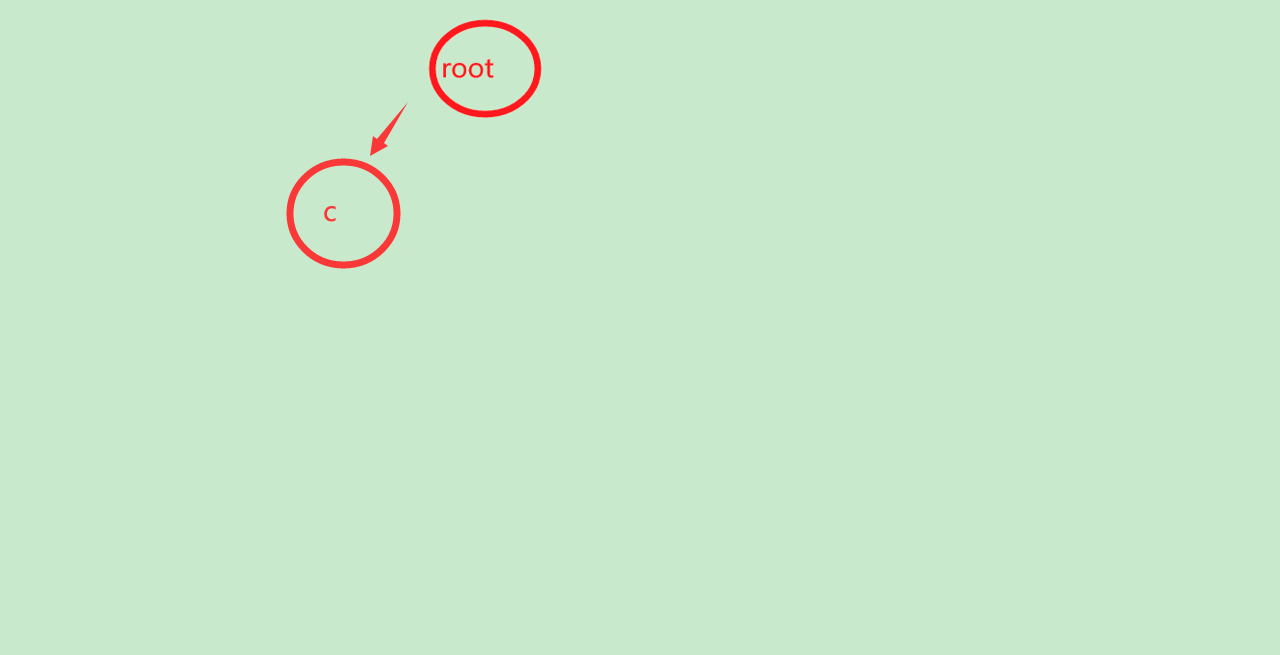
我们发现没有c，于是加入c，像查字典一样，我们先从最开始的字母找起

继续，我们找a

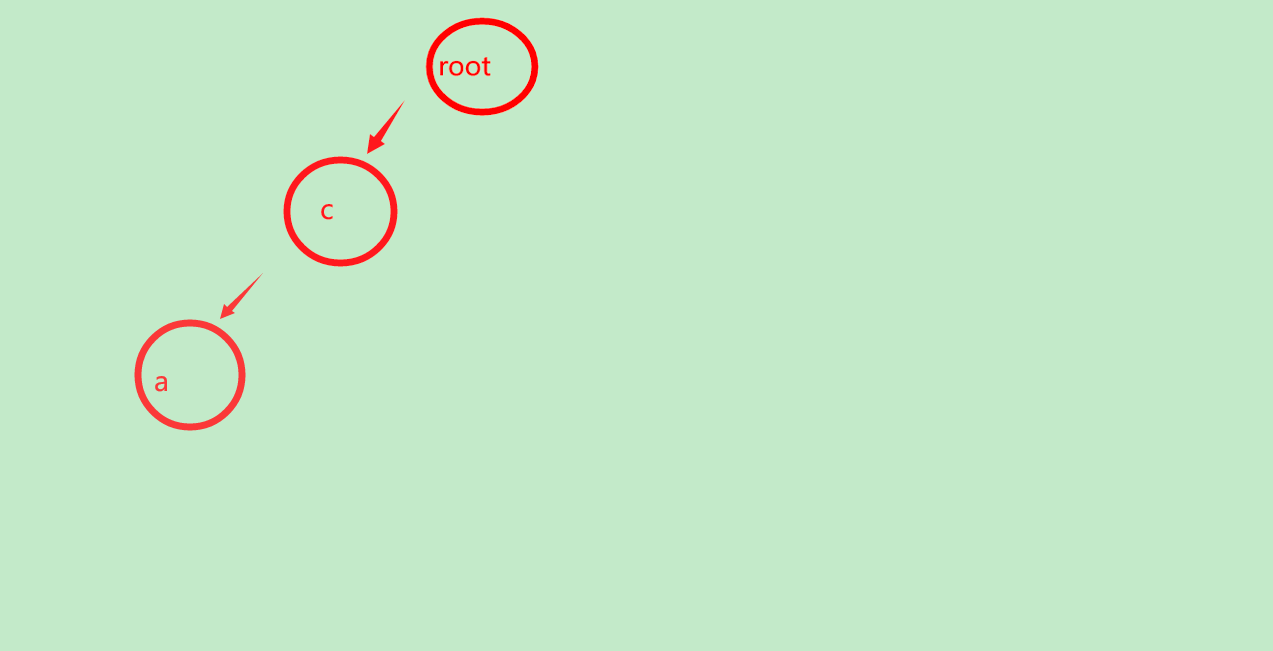
没有a，插入a

继续找t

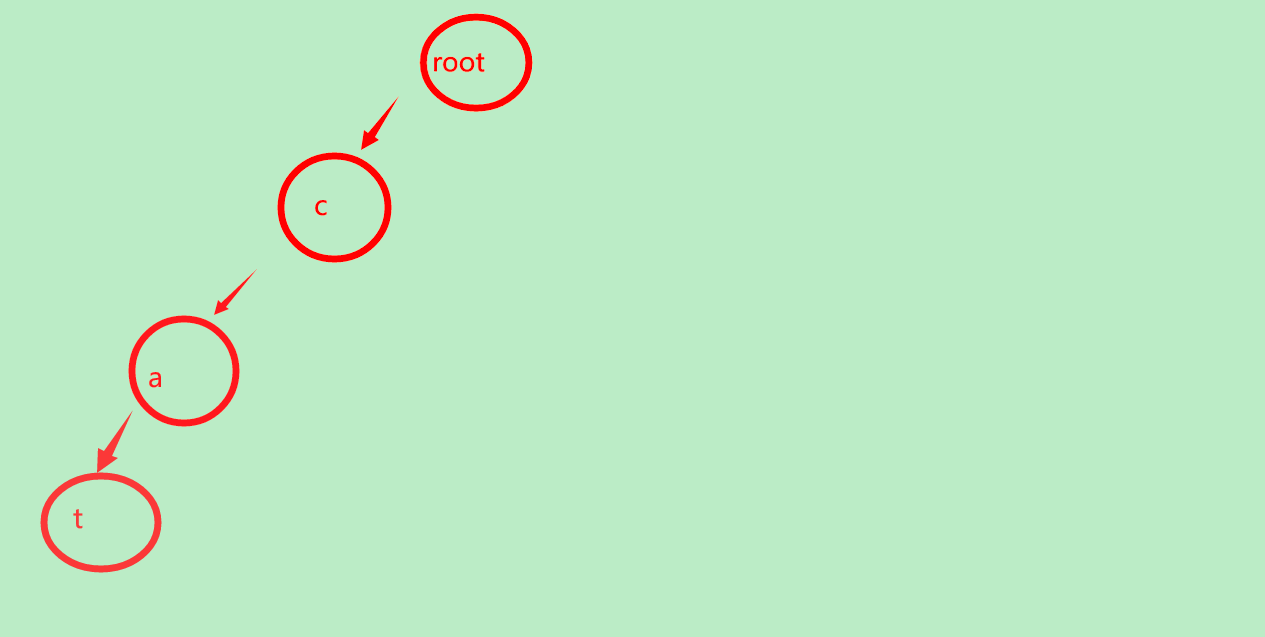
没有t，插入t

cat已经出现了！我们要在结尾的结点上标记，从根结点到此处存在单词

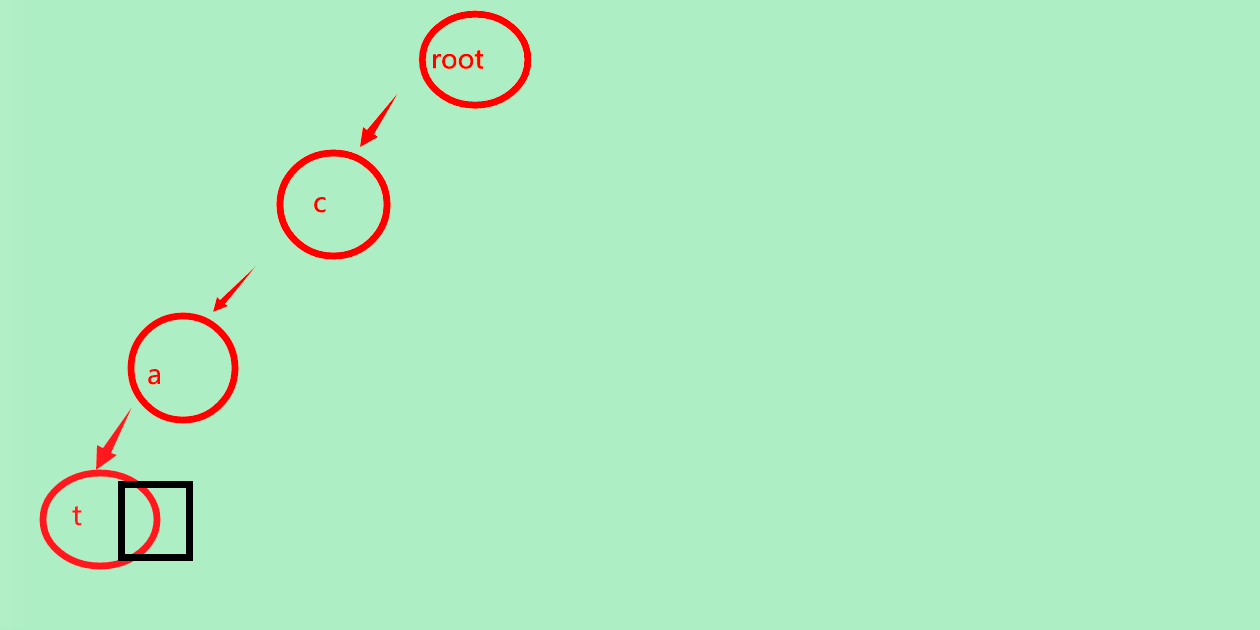
接下来找car：
我们发现，已经可以找到c和a，所以我们沿着c，a继续往下，找不到r，于是插入，标记

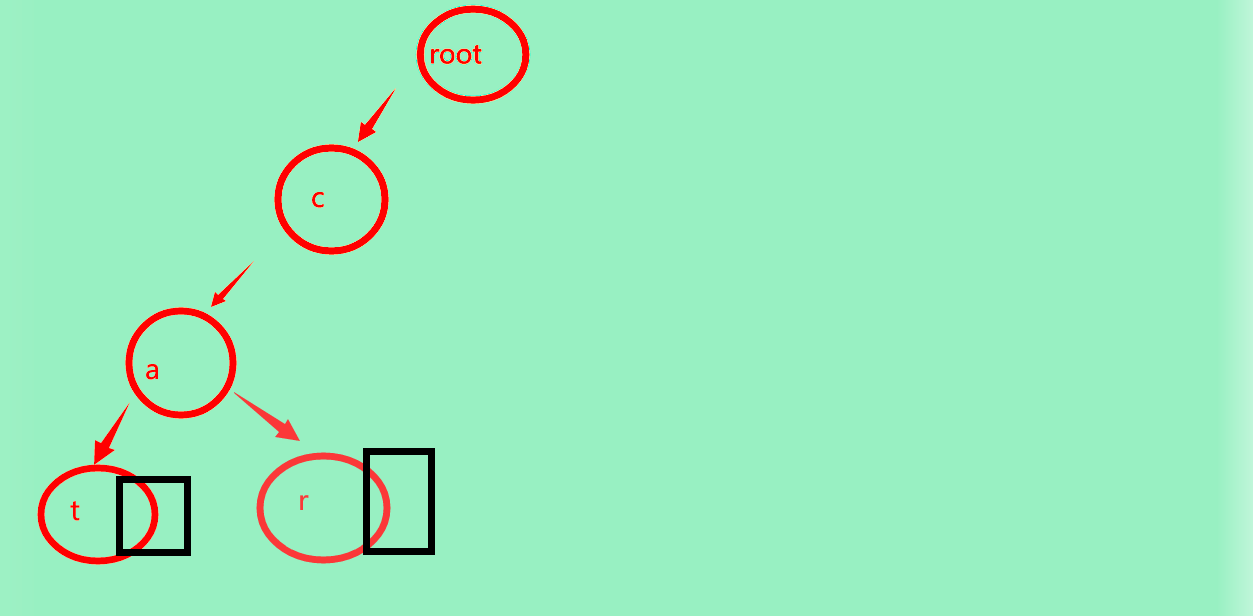
然后com和OK也是照葫芦画瓢：

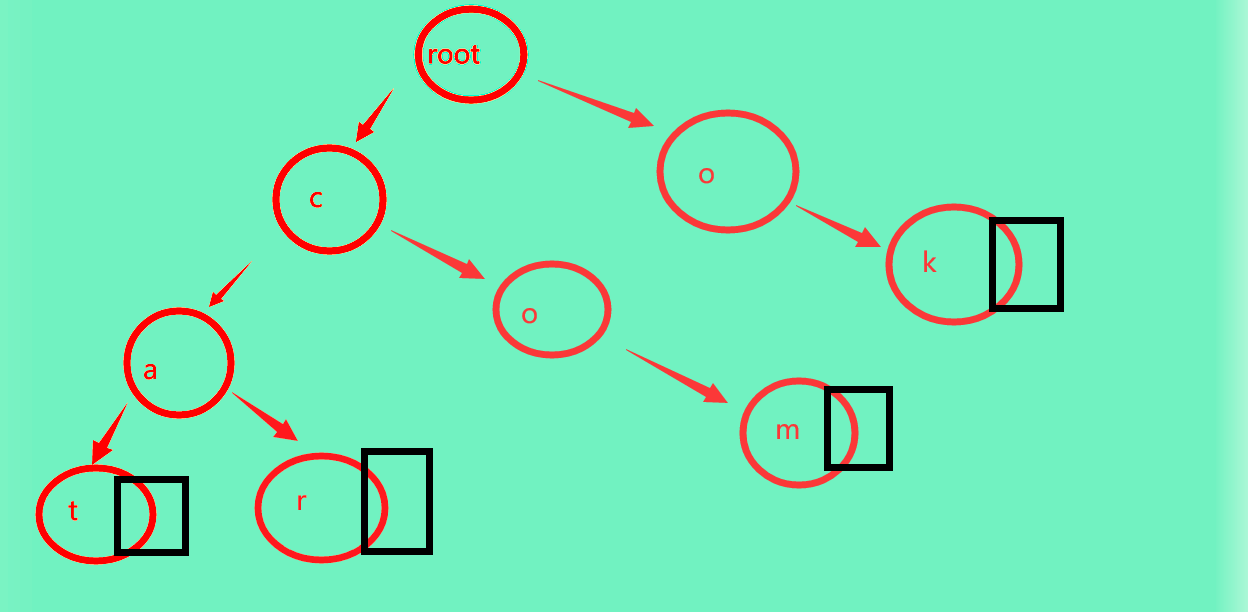
假如我们现在还想加入ca呢？

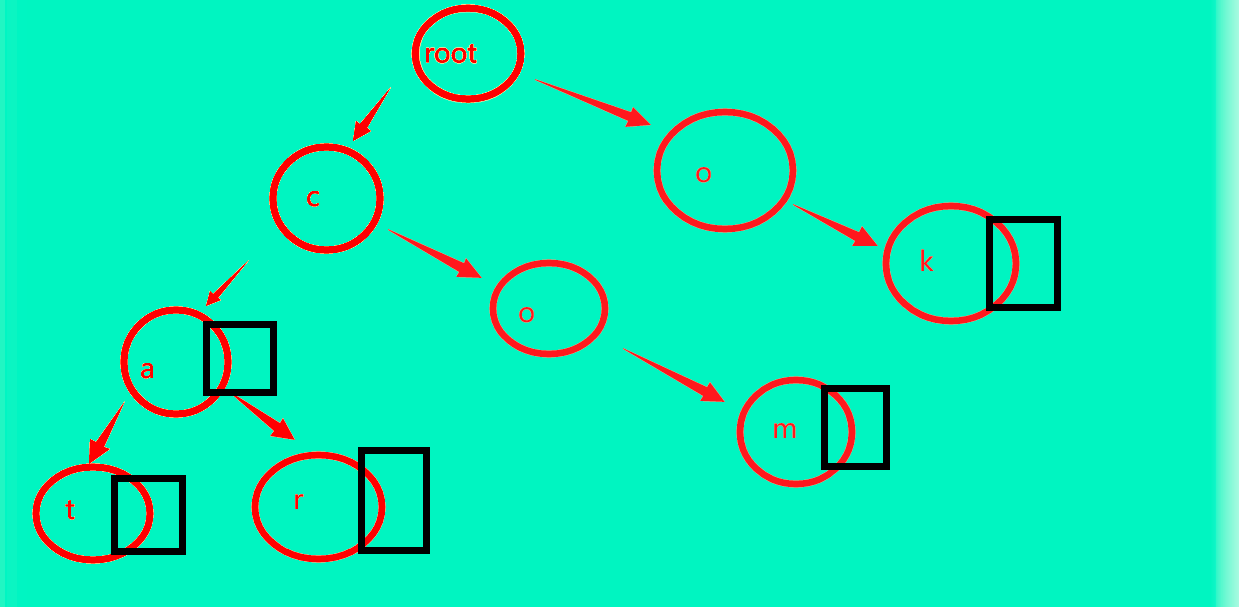
假如我们还想加入一个cat，并统计数量呢？

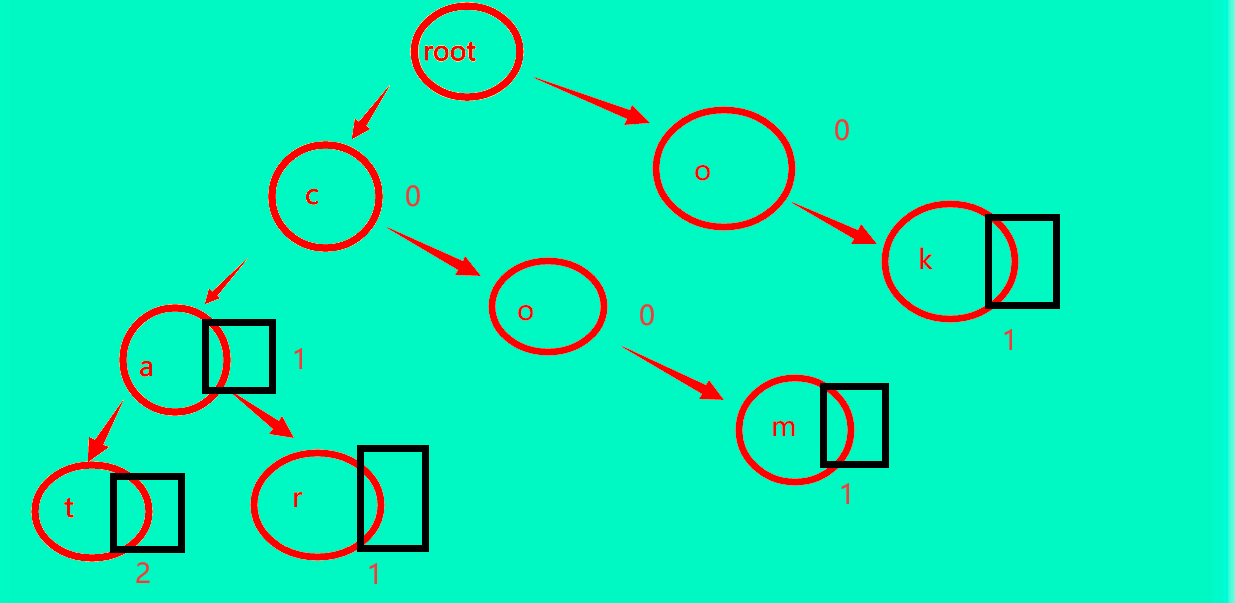
非常轻松非常愉快

查询也就更加简单，按照我们查字典的思路
先找一个开头字母
再到这个字母下找下一个字母
直到找到或者找不到路

删除em，很少用，如果你不闲占空间，就直接把标记去掉就好了
如果不想让他继续占空间，就只删除不是其他分支前缀的结点，像这样
首先判断该节点是不是还有其他子节点：
如果没有，判断它有没有标记
如果也没有，删掉，并且对其父节点进行相同操作，直到根节点

Over！

tire模板和实现

tire主要用给AC自动机来做数据结构，所以等到写AC自动机再补吧~_~