一、问题引入

给出一个长度为n的数组，完成以下两种操作：
1.单点修改：将第x个数加上k
2.区间查询：输出区间[l, r]内每个数的和

线段树$O(logn)$

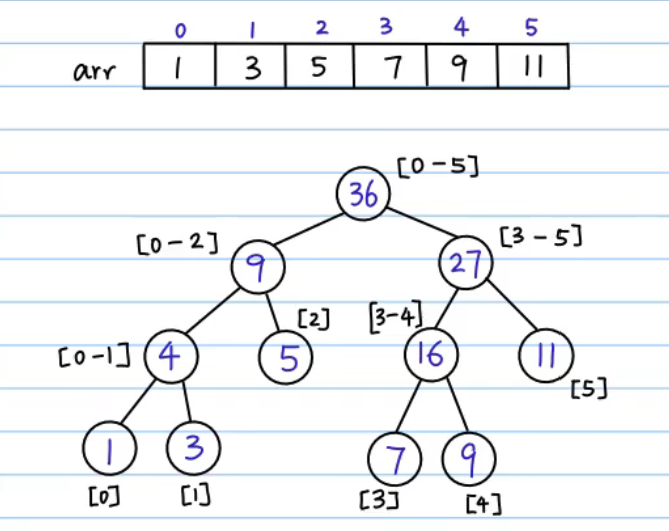
二、例题

单点修改、区间查询

敌兵布阵

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 50010;

int tree[N * 4];
int n;
int a[N];
int casei;

void build_tree(int node, int l, int r) {
    if (l >= r) {
        tree[node] = a[l];
        return;
    }

    int mid = (l + r) / 2;
    int left_node = node * 2;
    int right_node = node * 2 + 1;
    build_tree(left_node, l, mid), build_tree(right_node, mid + 1, r);
    tree[node] = tree[left_node] + tree[right_node];
}

void update_tree(int node, int l, int r, int idx, int val) {
    if (l >= r) {
        a[idx] += val;
        tree[node] += val;
        return;
    }

    int mid = (l + r) / 2;
    int left_node = node * 2;
    int right_node = node * 2 + 1;

    if (idx >= l && idx <= mid)
        update_tree(left_node, l, mid, idx, val);
    else
        update_tree(right_node, mid + 1, r, idx, val);
    tree[node] = tree[left_node] + tree[right_node];
}

int query_tree(int node, int l, int r, int start, int end) {
    if (l > end || r < start)
        return 0;
    else if (l >= start && r <= end)
        return tree[node];
    else if (l >= r)
        return tree[node];
    else {
        int mid = (l + r) / 2;
        int left_node = node * 2;
        int right_node = node * 2 + 1;
        return query_tree(left_node, l, mid, start, end) + query_tree(right_node, mid + 1, r, start, end);
    }
}

int main() {
    int T;
    scanf("%d", &T);

    while (T -- ) {
        printf("Case %d:\n", ++ casei);
        scanf("%d", &n);

        for (int i = 1; i <= n; i ++ )

            scanf("%d", &a[i]);
        build_tree(1, 1, n);
        char op[10];

        while (~scanf("%s", op)) {
            if (op[0] == 'E')
                break;
            int a, b;
            scanf("%d%d", &a, &b);

            if (op[0] == 'A')
                update_tree(1, 1, n, a, b);
            else if (op[0] == 'S')
                update_tree(1, 1, n, a, -b);
            else
                printf("%d\n", query_tree(1, 1, n, a, b));
        }
    }

    return 0;
}

区间修改、单点查询

Color the ball

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1e5 + 10;

int tree[N * 4];
int n;

void build_tree(int node, int l, int r) {
    if (l >= r) {
        tree[node] = 0;
        return;
    }

    int mid = (l + r) / 2;
    int left_node = node * 2;
    int right_node = node * 2 + 1;
    build_tree(left_node, l, mid), build_tree(right_node, mid + 1, r);
}

void update_tree(int node, int l, int r, int start, int end) {
    if (l == start && r == end) {
        tree[node] ++ ;
        return;
    }

    int mid = (l + r) / 2;
    int left_node = node * 2;
    int right_node = node * 2 + 1;

    if (end <= mid)
        update_tree(left_node, l, mid, start, end);
    else if (start > mid)
        update_tree(right_node, mid + 1, r, start, end);
    else {
        update_tree(left_node, l, mid, start, mid);
        update_tree(right_node, mid + 1, r, mid + 1, end);
    }
}

void query_tree(int node, int l, int r) {
    if (l >= r) {
        if (l != 1)
            printf(" ");
        printf("%d", tree[node]);
        return;
    }

    int mid = (l + r) / 2;
    int left_node = node * 2;
    int right_node = node * 2 + 1;

    if (tree[node]) {
        tree[left_node] += tree[node];
        tree[right_node] += tree[node];
        tree[node] = 0;
    }

    query_tree(left_node, l, mid), query_tree(right_node, mid + 1, r);
}

int main() {
    while (~scanf("%d", &n)) {
        if (n == 0)
            break;
        memset(tree, 0, sizeof tree);
        build_tree(1, 1, n);

        for (int i = 1; i <= n; i ++ ) {

            int a, b;
            scanf("%d%d", &a, &b);
            update_tree(1, 1, n, a, b);
        }

        query_tree(1, 1, n);
        puts("");
    }

    return 0;
}

区间修改、区间查询

A Simple Problem with Integers

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1e5 + 10;

typedef long long LL;

LL tree[N * 4];
LL add_Mark[N * 4];
LL arr[N * 4];
int n, m;
LL ans;

void build_tree(int node, int l, int r) {
    add_Mark[node] = 0;

    if (l == r) {
        tree[node] = arr[l];
        return;
    }

    int mid = (l + r) / 2;
    int left_node = node * 2;
    int right_node = node * 2 + 1;
    build_tree(left_node, l, mid), build_tree(right_node, mid + 1, r);
    tree[node] = tree[left_node] + tree[right_node];
}

void update_tree_son(int node, int l, int r) {
    int mid = (l + r) / 2;
    int left_node = node * 2;
    int right_node = node * 2 + 1;

    if (add_Mark[node]) {
        add_Mark[left_node] += add_Mark[node];
        add_Mark[right_node] += add_Mark[node];
        tree[left_node] += add_Mark[node] * (mid - l + 1);
        tree[right_node] += add_Mark[node] * (r - (mid + 1) + 1);
        add_Mark[node] = 0;
    }
}

void update_tree(int node, int l, int r, int start, int end, LL val) {
    if (l >= start && r <= end) {
        add_Mark[node] += val;
        tree[node] += (r - l + 1) * val;
        return;
    }

    int mid = (l + r) / 2;
    int left_node = node * 2;
    int right_node = node * 2 + 1;
    update_tree_son(node, l, r);

    if (l == r)
        return;

    if (end <= mid)
        update_tree(left_node, l, mid, start, end, val);
    else if (start > mid)
        update_tree(right_node, mid + 1, r, start, end, val);
    else {
        update_tree(left_node, l, mid, start, mid, val);
        update_tree(right_node, mid + 1, r, mid + 1, end, val);
    }

    tree[node] = tree[left_node] + tree[right_node];
}

void query_tree(int node, int l, int r, int start, int end) {
    if (l >= start && r <= end) {
        ans += tree[node];
        return;
    }

    int mid = (l + r) / 2;
    int left_node = node * 2;
    int right_node = node * 2 + 1;
    update_tree_son(node, l, r);

    if (l == r)
        return;

    if (end <= mid)
        query_tree(left_node, l, mid, start, end);
    else if (start > mid)
        query_tree(right_node, mid + 1, r, start, end);
    else {
        query_tree(left_node, l, mid, start, mid);
        query_tree(right_node, mid + 1, r, mid + 1, end);
    }
}

int main() {
    scanf("%d%d", &n, &m);

    for (int i = 1; i <= n; i ++ )

        scanf("%lld", &arr[i]);
    build_tree(1, 1, n);
    char op[2];

    while (m -- ) {
        scanf("%s", op);

        if (op[0] == 'C') {
            int a, b;
            LL c;
            scanf("%d%d%lld", &a, &b, &c);
            update_tree(1, 1, n, a, b, c);
        } else {
            int a, b;
            scanf("%d%d", &a, &b);
            ans = 0;
            query_tree(1, 1, n, a, b);
            printf("%lld\n", ans);
        }
    }

    return 0;
}

单点修改、区间查询(维护最值)

I Hate It

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 2e5 + 10;

int tree[N * 4], arr[N * 4];
int n, m;

void build_tree(int node, int l, int r) {
    if (l >= r) {
        tree[node] = arr[l];
        return;
    }

    int mid = (l + r) / 2;
    int left_node = 2 * node;
    int right_node = 2 * node + 1;
    build_tree(left_node, l, mid), build_tree(right_node, mid + 1, r);
    tree[node] = max(tree[left_node], tree[right_node]);
}

void update_tree(int node, int l, int r, int idx, int val) {
    if (l >= r) {
        arr[idx] = val;
        tree[node] = val;
        return;
    }

    int mid = (l + r) / 2;
    int left_node = 2 * node;
    int right_node = 2 * node + 1;

    if (idx <= mid)
        update_tree(left_node, l, mid, idx, val);
    else
        update_tree(right_node, mid + 1, r, idx, val);
    tree[node] = max(tree[left_node], tree[right_node]);
}

int query_tree(int node, int l, int r, int start, int end) {
    int res = 0;

    if (l >= start && r <= end) {
        return tree[node];
    }

    int mid = (l + r) / 2;
    int left_node = 2 * node;
    int right_node = 2 * node + 1;

    if (start <= mid)
        res = max(res, query_tree(left_node, l, mid, start, end));

    if (mid < end)
        res = max(res, query_tree(right_node, mid + 1, r, start, end));
    return res;
}

int main() {
    while (~scanf("%d%d", &n, &m)) {
        memset(tree, 0, sizeof tree);

        for (int i = 1; i <= n; i ++ )

            scanf("%d", &arr[i]);
        build_tree(1, 1, n);
        char op[2];
        int a, b;

        while (m -- ) {
            scanf("%s%d%d", op, &a, &b);

            if (op[0] == 'Q')
                printf("%d\n", query_tree(1, 1, n, a, b));
            else
                update_tree(1, 1, n, a, b);
        }
    }

    return 0;
}

求逆序对

Minimum Inversion Number

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 5010, INF = 0x3f3f3f3f;

typedef long long LL;

int tree[N * 4], arr[N * 4];
int n;

void build_tree(int node, int l, int r) {
    if (l >= r) {
        tree[node] = 0;
        return;
    }

    int mid = (l + r) / 2;
    int left_node = 2 * node;
    int right_node = 2 * node + 1;
    build_tree(left_node, l, mid), build_tree(right_node, mid + 1, r);
    tree[node] = tree[left_node] + tree[right_node];
}

void update_tree(int node, int l, int r, int val) {
    if (l >= r) {
        tree[node] ++ ;
        return;
    }

    int mid = (l + r) / 2;
    int left_node = 2 * node;
    int right_node = 2 * node + 1;

    if (val <= mid)
        update_tree(left_node, l, mid, val);
    else
        update_tree(right_node, mid + 1, r, val);
    tree[node] = tree[left_node] + tree[right_node];
}

int query_tree(int node, int l, int r, int start, int end) {
    int res = 0;

    if (l >= start && r <= end) {
        return tree[node];
    }

    int mid = (l + r) / 2;
    int left_node = 2 * node;
    int right_node = 2 * node + 1;

    if (start <= mid)
        res += query_tree(left_node, l, mid, start, end);

    if (mid < end)
        res += query_tree(right_node, mid + 1, r, start, end);
    return res;
}

int main() {
    while (~scanf("%d", &n)) {
        memset(tree, 0, sizeof tree);

        for (int i = 1; i <= n; i ++ )

            scanf("%d", &arr[i]);
        build_tree(1, 1, n);
        LL ans = INF;
        LL cnt = 0;

        for (int i = 1; i <= n; i ++ ) {

            cnt += query_tree(1, 1, n, arr[i] + 1, n);
            update_tree(1, 1, n, arr[i] + 1);
        }

        ans = cnt;

        for (int i = 1; i <= n; i ++ ) {

            cnt = cnt - arr[i] + n - 1 - arr[i];
            ans = min(ans, cnt);
        }

        printf("%lld\n", ans);
    }

    return 0;
}

单点更新

Billboard

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 2e5 + 10;

int h, w, n;
int tree[N * 10], arr[N];

void build_tree(int node, int l, int r) {
    if (l >= r) {
        tree[node] = w;
        return;
    }

    int mid = (l + r) / 2;
    int left_node = 2 * node;
    int right_node = 2 * node + 1;
    build_tree(left_node, l, mid), build_tree(right_node, mid + 1, r);
    tree[node] = max(tree[left_node], tree[right_node]);
}

int update_query_tree(int node, int l, int r, int val) {
    if (l >= r) {
        tree[node] -= val;
        return l;
    }

    int res = 0;
    int mid = (l + r) / 2;
    int left_node = 2 * node;
    int right_node = 2 * node + 1;

    if (tree[left_node] >= val)
        res = update_query_tree(left_node, l, mid, val);
    else
        res = update_query_tree(right_node, mid + 1, r, val);
    tree[node] = max(tree[left_node], tree[right_node]);
    return res;
}

int main() {
    while (~scanf("%d%d%d", &h, &w, &n)) {
        if (h > n)
            h = n;
        memset(tree, 0, sizeof tree);
        build_tree(1, 1, h);

        for (int i = 1; i <= n; i ++ ) {

            scanf("%d", &arr[i]);

            if (arr[i] > tree[1])
                puts("-1");
            else
                printf("%d\n", update_query_tree(1, 1, h, arr[i]));
        }
    }

    return 0;
}

插队问题

Buy Tickets

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 2e5 + 10;

struct node {
    int pos, val;
} person[N];

int tree[N * 4];
int n;
int ans[N];

void build_tree(int k, int l, int r) {
    if (l >= r) {
        tree[k] = 1;
        return;
    }

    int mid = (l + r) / 2;
    int ls = k * 2;
    int rs = k * 2 + 1;
    build_tree(ls, l, mid), build_tree(rs, mid + 1, r);
    tree[k] = tree[ls] + tree[rs];
}

void update_tree(int k, int l, int r, int idx, int val) {
    if (l >= r) {
        tree[k] = 0;
        ans[l] = val;
        return;
    }

    int mid = (l + r) / 2;
    int ls = k * 2;
    int rs = k * 2 + 1;

    if (tree[ls] >= idx)
        update_tree(ls, l, mid, idx, val);
    else
        update_tree(rs, mid + 1, r, idx - tree[ls], val);
    tree[k] = tree[ls] + tree[rs];
}

int main() {
    while (~scanf("%d", &n)) {
        memset(tree, 0, sizeof tree);

        for (int i = 1; i <= n; i ++ )

            scanf("%d%d", &person[i].pos, &person[i].val);
        build_tree(1, 1, n);

        for (int i = n; i; i -- )

            update_tree(1, 1, n, person[i].pos + 1, person[i].val);

        for (int i = 1; i <= n; i ++ ) {

            if (i != n)
                printf("%d ", ans[i]);
            else
                printf("%d\n", ans[i]);
        }
    }

    return 0;
}