最大公约数——欧几里得算法

原理：
d能整除a,b, 则d能整除 ax + by
a % b = a - (a / b) * b // a / b 代表下取整
(a, b) 的最大公约数 = ( b, a % b )的最大公约数

int gcd(int a, int b) {
  if (b == 0) return a;
  return gcd(b, a % b);
}

最小公倍数——lcm

gcd(a, b) * lcm(a, b) = a * b
lcm(a, b) = a * b / gcd(a, b);

扩展欧几里得算法

求满足 $$ ax + by = gcd(a, b) $$ 的一组解

a % b = a - c * b, c = a / b ( 下取整 )

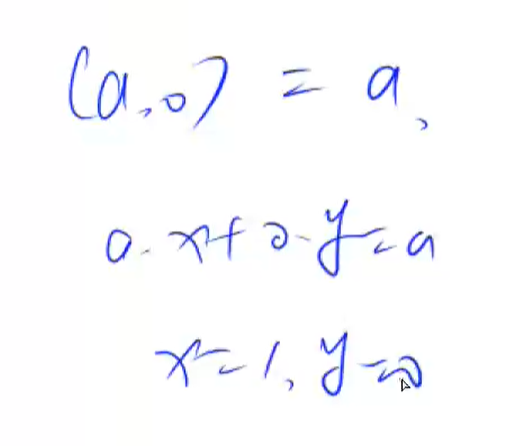
int exgcd(int a, int b, int &x, int &y)  // 扩展欧几里得算法, 求x, y，使得ax + by = gcd(a, b)
{
    if (!b)
    {
        x = 1; y = 0;
        return a;
    }
    int d = exgcd(b, a % b, y, x); // 反向递归
    // y -> x2, x -> y2
    y = y - (a / b) * x;
    return d;
}

int exgcd(int a, int b, int &x, int &y) {
  if (!b) {
    x = 1;
    y = 0;
    return a;
  }
  int d = exgcd(b, a % b, x, y); // 正向递归
  int t = x;
  x = y;
  y = t - (a / b) * y;
  return d;
}

扩展欧几里得算法求线性同余方程 / 求逆元

证明：

求逆元即 $$ ax ≡ 1 $$