深入浅出ST表
现在马上打开脑子,我们从一个问题开始!
设计一个算法,完成对一个数组a的第i个和第j个数之间最大的数的查找
这好说啊,我们再a数组里头一个一个找最大的就是了呗
确实,一般情况就会选择这种方法
但是如果我要求对数组a进行多次查询,每次给一个l,r求区间内最大值呢?
这个方法很显然不是那么友好,因为每一次都要查询O(r-l)次
如果全国的同学都要查12日到30日的最高气温,那该慢到那里去?
这个问题,就是非常经典的RMQ(区间最值问题)问题
而对于这个问题,我们将会介绍一个非常实用的数据结构:ST表
打表× ST表√
ST表之前,我们用的是打表法来处理静态区间最值问题
所谓打表,就是在你询问之前就提前准备好我的答案,你问什么答什么
这样子非常好,一问答案就出,不需要思考,因为提前准备好了
但是,这又有一个弊端:你需要背下所有的答案
如果题目的范围很大,那么很显然,背下所有这些答案并不是一件容易的事
即会花费很多的空间,又会花费大量时间
最重要的是,我背了它还不一定都会考TAT
所以,这样就很难受,于是,我们开始想办法:我们能不能少背一点呢?
经过大佬们的思考,答案是,我们确实可以少背一点
但是少背题的条件是,题目必须可以被分解和合并
比如:问题是全世界最高的山有多高
我们就可以只背北半球最高的山,南半球最高的山,然后现场比较一下就可以了
这样,我们需要比较一下,但是我们可以少背一点啦!
这就是ST算法的一个基础:可重
然而,就算这样,也并没有多好的效果
因为更重要的一点是:倍增
不扯犊子了,回到数组a
随便写一个: 1001 2 3432 23 -23 232
如果按照上文的说法,我们要求[0,5]的区间最大值,我们只需要提前备好[0,2]和[3,5]的区间最大值就可以了
但是如果我们要求所有的,我们要背的其实也不少
我们还想少背一点!
于是,我们有了倍增思想的ST表
它是怎么背的呢?
st[i][j]将会表示从i开始,长2^j的数组长度
有什么效果呢?
首先,我们只需要背nlogn的题量了,比起前面的n^2少了不少
那,我们背了之后怎么用呢?
先看式子:
maxs[i][j]=max{st[i][log(2,(j-i+1))],st[j-(1 << log(2,(j-i+1))+1][log(2,(j-i+1))]}
很长,看不懂,没关系,看图!
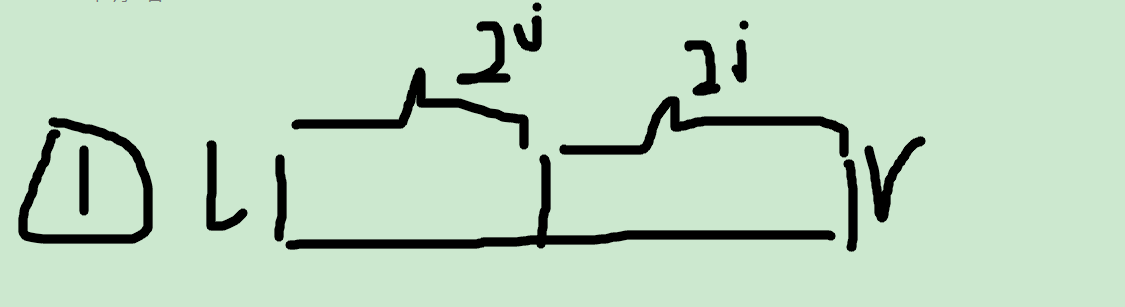
首先,我们看到log(2,(j-i+1))是什么,j-i+1是整个查询范围的长度,我们设它为len
那么log(2,len)就是指以2为底的len的对数,实际上就是表示2的几次方是不大于len的最大数
也就是得到一个指数k,满足2^k小于等于len,并且2* 2^k 大于等于len
第一个区间st[i][log(2,(j-i+1))]就是表示从i开始,长度为2^k位的区间最值
而第二个区间:st[j-(1 << log(2,(j-i+1))+1][log(2,(j-i+1))]
简化一下就是st[j-2^k+1][k]
这下是不是就很好理解了!就是以j结束的长度位2^k的区间最值啊!
实际上呢,也就是:
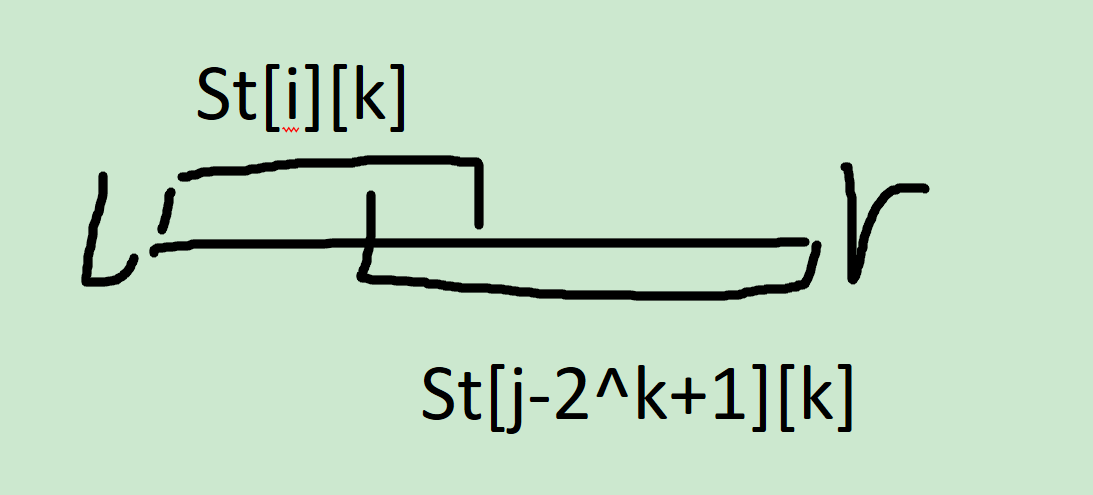
妈呀OneNote的画图功能也太蛋疼了吧,谁来救救我TAT
总之,这两个区间最大值的最大值,还能不是总最大值?
就好像1班第一和二班第一中更高的那个,难道不是1,2班的第一?
这就是可重的道理
而选择用2的次方就很巧妙了,这就是倍增的思想
其实就是因为用2的次方可以满足只需要两个区间的最值合并就可以了,而且2的指数分布的比较好
那么,ST表怎么查知道了,ST表该怎么建呢?
首先,ST表也是一个静态的表,所以,生成了ST表后,再更改数组,ST表就失效了!
其实生成ST表和查询ST表是一样的道理啦!
首先初始话,st[i][0]=arr[i]就可以了!
然后,其实就是一个查表的过程,只要把结果记录好就可以了!(逐渐提高j)
st[i][j]=max(st[i][j-1],st[i+(1<<(j-1))][j-1])
仔细看:本质上还是查表哦!
水平所限,以后更新^_^
Over~

