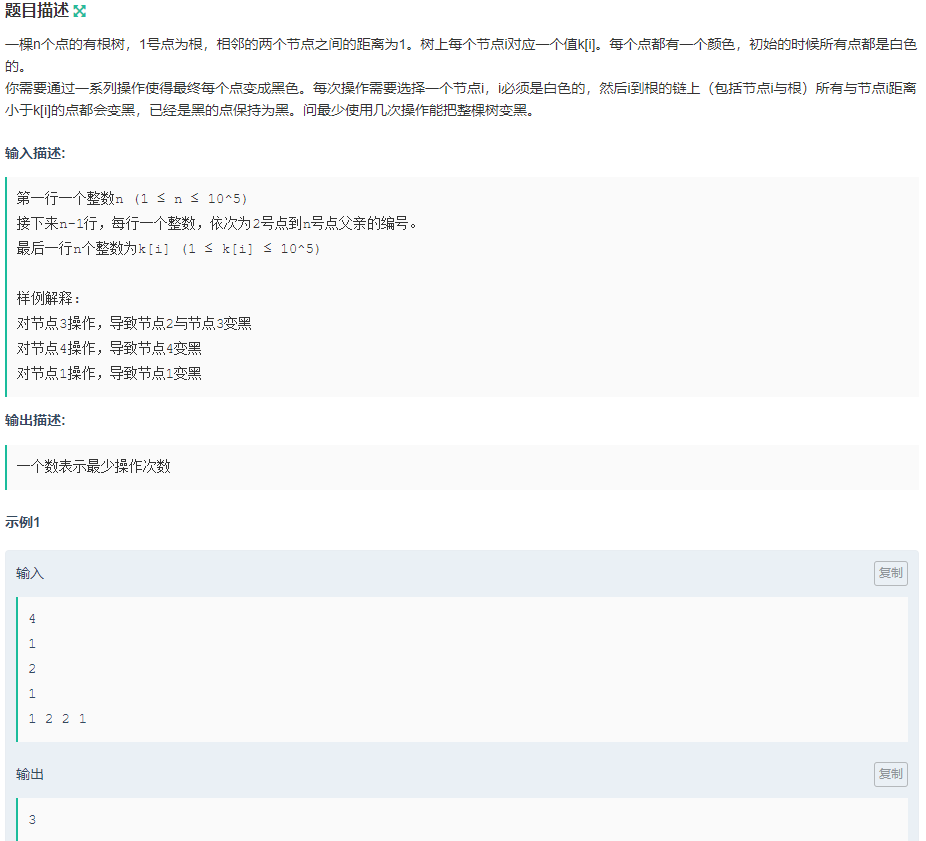
$$首先，每个节点只能改变向上方向的颜色，所以叶子节点必选$$
$$其次我们考虑贪心，是不是每次我们覆盖不到当前点的时候，就把当前点选上是最优的呢？$$
$$显然是错的，如果某个被染色过的k值很大，且我们没有选过他，那么我们再次选他的时候一定会更优$$
$$所以遍历整颗树，同时维护f，k数组，k代表当前结点能够向上拓展的最远距离$$
$$f数组表示所有子节点能覆盖到的最远，如果f[u] = 0, 即表示当前点没被染黑，必须选一个子树中的最优点$$

#include <bits/stdc++.h>

using namespace std;

const int N = 1e5 + 10;

int k[N], f[N];
int n;
int ans;
vector<int> g[N];

void dfs(int u, int fa)
{
    for(int i = 0; i < g[u].size(); i ++)
    {
        int j = g[u][i];

        dfs(j, u);
        k[u] = max(k[u], k[j] - 1);
        f[u] = max(f[u], f[j] - 1);
    }

    if(!f[u])
    {
        ans ++;
        f[u] = k[u];
    }
}

int main()
{
    cin >> n;

    for(int i = 2; i <= n; i ++)
    {
        int x;
        cin >> x;
        g[x].push_back(i);
        //g[i].push_back(x);
    }

    for(int i = 1; i <= n; i ++) cin >> k[i];

    dfs(1, -1);

    cout << ans << endl;
}